
- •2.Уравнение Бернули
- •3. Теорема Лейбница
- •1.Полный дифференциал функции нескольких переменных
- •3. Признак Даламбера сходимости знакоположительных рядов
- •1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
- •2.Методы интегрирования определенных интегралов
- •3. Знакопеременные ряды. Теорема об абсолютной сходимости
- •1.Производная функции по направлению
- •1. Вывод формулы Тейлора
- •2. Второй признак сравнения знакоположительных рядов
- •3. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница.Гамма-функция
- •2. Дифференциальные уравнения с разделяющимися переменными.
Билет 11.
№1.
Множества и т.д.:
Множеством
называется совокупность некоторых
элементов. Элементами множества могут
быть числа, фигуры, предметы, понятия и
т. п. Множество может быть задано одним
из двух способов: перечислением и с
помощью определяющего свойства.
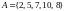
множество чисел. В общем случае множество
элементов х с помощью определяющего
свойства f(x)
записывается в виде
множество чисел. В общем случае множество
элементов х с помощью определяющего
свойства f(x)
записывается в виде
 .
Если множество не содержит ни одного
элемента, то оно называется пустым
множеством и записывается
.
Если множество не содержит ни одного
элемента, то оно называется пустым
множеством и записывается
 .
Квантором
называется логический символ, который
характеризует следующие за ним элементы
в количественном отношении.
квантор общности, используется вместо
слов «для всех,
квантор существования, используется
вместо слов «существует». Операции
над множествами:
Два множества А и В равны,если они состоят
из одних и тех же элементов. Объединением
(суммой) множеств А и В называется
множество А
В, элементы которого принадлежат хотя
бы одному из этих множеств. Пересечением
(произведением) множеств А и В называется
множество А
В, элементы которого принадлежат как
множеству А, так и множеству В.Разностью
множеств А и В называется множество А
\ В, элементы которого принадлежат
множеству А, но не принадлежат множеству
В.Симметрической разностью множеств
А и В называется множество А Δ В,
являющееся объединением разностей
множеств А \ В и В \А , т. е. А Δ В = (А \ В)
(В \А).
Свойства операций над множествами:
1. Свойство перестановочности
(коммутативность) для объединения и
пересечения множеств, т. е. А
В = В
А; А
В = В
А. 2. Сочетательное свойство (ассоциативность)
для объединения и пересечения множеств,
т. е. (А
В)
С= А
(В
С); (А
В)
С= А
(ВС).
3. Распределительное свойство
(дистрибутивность) для объединения и
пересечения множеств: 1) (А
В)
С= (А
С)
(В
С);
.
Квантором
называется логический символ, который
характеризует следующие за ним элементы
в количественном отношении.
квантор общности, используется вместо
слов «для всех,
квантор существования, используется
вместо слов «существует». Операции
над множествами:
Два множества А и В равны,если они состоят
из одних и тех же элементов. Объединением
(суммой) множеств А и В называется
множество А
В, элементы которого принадлежат хотя
бы одному из этих множеств. Пересечением
(произведением) множеств А и В называется
множество А
В, элементы которого принадлежат как
множеству А, так и множеству В.Разностью
множеств А и В называется множество А
\ В, элементы которого принадлежат
множеству А, но не принадлежат множеству
В.Симметрической разностью множеств
А и В называется множество А Δ В,
являющееся объединением разностей
множеств А \ В и В \А , т. е. А Δ В = (А \ В)
(В \А).
Свойства операций над множествами:
1. Свойство перестановочности
(коммутативность) для объединения и
пересечения множеств, т. е. А
В = В
А; А
В = В
А. 2. Сочетательное свойство (ассоциативность)
для объединения и пересечения множеств,
т. е. (А
В)
С= А
(В
С); (А
В)
С= А
(ВС).
3. Распределительное свойство
(дистрибутивность) для объединения и
пересечения множеств: 1) (А
В)
С= (А
С)
(В
С);
Декартово
произведение множеств.
Декартовым произведением множеств
называется множество точек
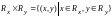 .
Модуль
числа, его свойства:
По определению
.
Модуль
числа, его свойства:
По определению
 1)
1)
 ;
2)
;
2)
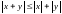 ;
3)
;
3)
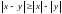 или
или
 ;
4)
;
4)
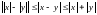 .
Грани
числовых множеств:
Число К называется верхней гранью
множества А, если
.
Грани
числовых множеств:
Число К называется верхней гранью
множества А, если
 .
Если С > 0, то К + С также является верхней
гранью этого множества. Число k
называется нижней гранью множества А,
если
.
Если С > 0, то К + С также является верхней
гранью этого множества. Число k
называется нижней гранью множества А,
если
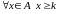 .
Если С > 0, то k
С также является нижней гранью этого
множества. Счетные
и несчетные множества:
Для того, чтобы сравнить два каких-либо
множества А и В, между их элементами
устанавливают соответствие. Если это
соответствие взаимнооднозначное, то
множества называются эквивалентными
или равномощными, А
В или А
В. Последовательностью
называется множество чисел, перенумерованных
с помощью натуральных чисел и расставленных
в порядке возрастания их номеров
.
Если С > 0, то k
С также является нижней гранью этого
множества. Счетные
и несчетные множества:
Для того, чтобы сравнить два каких-либо
множества А и В, между их элементами
устанавливают соответствие. Если это
соответствие взаимнооднозначное, то
множества называются эквивалентными
или равномощными, А
В или А
В. Последовательностью
называется множество чисел, перенумерованных
с помощью натуральных чисел и расставленных
в порядке возрастания их номеров
 .
Счетным
множеством
называется множество эквивалентное
множеству натуральных чисел.
.
Счетным
множеством
называется множество эквивалентное
множеству натуральных чисел.
№2. Формула Тейлора. Остаточный член в форме Лагранжа и Пеано.
Если в некоторой окрестности точки х = а функция y=f(x) имеет конечные производные до (n+1)-го порядка включительно, то для любой точки этой окрестности справедлива формула
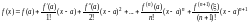 ,
где
,
где
 .
. .
Данное выражение для
.
Данное выражение для
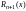 называется остаточным членом в форме
Лагранжа. Если представить
в виде
называется остаточным членом в форме
Лагранжа. Если представить
в виде
 ,
где
,
где
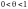 ,
то остаточный член примет вид
,
то остаточный член примет вид
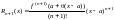 .
В частном случае, если
.
В частном случае, если
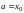 ,
,
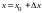 ,
то формула Тейлора примет вид
,
то формула Тейлора примет вид
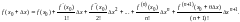 При
n
= 0 из формулы Тейлора получается формула
теоремы Лагранжа о конечном приращении
функции
При
n
= 0 из формулы Тейлора получается формула
теоремы Лагранжа о конечном приращении
функции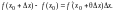 .Найдем
.Найдем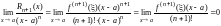 ,
т. е. остаточный член
,
т. е. остаточный член
 является бесконечно малой функцией по
сравнению с
является бесконечно малой функцией по
сравнению с
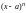 .
Поэтому его можно кратко записать
следующим образом
.
Поэтому его можно кратко записать
следующим образом
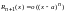 .
Данная запись остаточного члена
называется в форме Пеано.
.
Данная запись остаточного члена
называется в форме Пеано.
№3.
Числовые ряды. Необходимый признак
сходимости.
Числовой
ряд
– это сумма членов числовой
последовательности вида
![]() .
Если числовой ряд
.
Если числовой ряд
![]() сходится,
то предел его k-ого
члена равен нулю:
сходится,
то предел его k-ого
члена равен нулю:
![]() ,если
,если
![]() ,
то ряд расходится.
,
то ряд расходится.
1.
Если сходится числовой ряд
,
то сходящимся будет и ряд
![]() .
Другими словами, сходящимся будет и ряд
без первых m
членов. Если к сходящемуся числовому
ряду
добавить
несколько членов (от первого до m-ого),
то полученный ряд также будет сходящимся.
.
Другими словами, сходящимся будет и ряд
без первых m
членов. Если к сходящемуся числовому
ряду
добавить
несколько членов (от первого до m-ого),
то полученный ряд также будет сходящимся.
2.Если
сходится числовой ряд
и
его сумма равна S,
то сходящимся будет и ряд
![]() ,
причем
,
причем
![]() ,
где A
– произвольная постоянная. 3.Если
сходятся числовые ряды
и
,
где A
– произвольная постоянная. 3.Если
сходятся числовые ряды
и
![]() ,
их суммы равны A
и B
соответственно, то сходящимися будут
ряды
,
их суммы равны A
и B
соответственно, то сходящимися будут
ряды
![]() и
и
![]() ,
причем их суммы будут равны A
+ B
и A
- B
соответственно.
,
причем их суммы будут равны A
+ B
и A
- B
соответственно.
Билет 12.
1.
Необходимые условия дифференцируемости функций нескольких переменных.
Теорема.
Если функция нескольких переменных, дифференцируемая в некоторой точке, то она непрерывна в этой точке.
Доказательство.
По определению, функция является
непрерывной, если
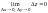 .
Найдем
.
Найдем
 .Следовательно,
.Следовательно,
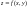 непрерывная.
непрерывная.
Теорема.Если функция нескольких переменных, дифференцируемая в точке, то она имеет частные производные в этой точке.
Доказательство.
Пусть
 дифференцируемая. Если y
=
const,
то y
= 0. Тогда
дифференцируемая. Если y
=
const,
то y
= 0. Тогда

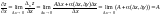 .
.
Если
x
=
const,
то x
=
0. Тогда .
.
2.Уравнение Бернули
В
общем случае уравнение Бернулли имеет
вид
 ,
,
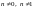 ,
здесь
,
здесь
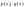
непрерывные функции.
непрерывные функции.
Поделим
уравнение на
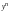 ,
получим
,
получим
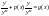 .
.
Данное уравнение приводится к линейному уравнению с помощью подстановки
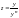 или
или
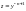 .
.
Найдем

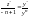 и подставим в исходное уравнение, получим
линейное уравнение относительно
переменной z.
и подставим в исходное уравнение, получим
линейное уравнение относительно
переменной z.
 .
.
3. Теорема Лейбница
Если
члены знакочередующегося ряда
 монотонно
убывают
монотонно
убывают
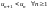 и стремятся к нулю
и стремятся к нулю
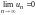 ,
то ряд сходится; причем сумма ряда по
абсолютной величине не превосходит
первого члена ряда
,
то ряд сходится; причем сумма ряда по
абсолютной величине не превосходит
первого члена ряда
 .
.
Доказательство. По определению знакочередующегося ряда


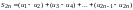 .
.
Так
как члены ряда монотонно убывают ( ),
то разность в каждой скобке суммы
),
то разность в каждой скобке суммы
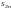 больше нуля и эта сумма монотонно
возрастает с увеличением числа членов
2n
больше нуля и эта сумма монотонно
возрастает с увеличением числа членов
2n
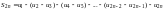 .
.
Так
как в этой сумме также разность в каждой
скобке больше нуля, то сумма монотонно
убывает с увеличением числа членов 2n
и не превосходит первого члена ряда
 .
.
предел частичных сумм ряда с нечетным числом членов.
 .
.
При
нечетном числе членов ряда сумма
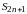 также не превосходит первого члена ряда
также не превосходит первого члена ряда
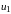 .
.
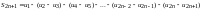 .
.
Таким образом, предел частичных сумм знакочередующегося ряда существует, т. е. ряд всегда сходится, если его члены монотонно убывают и стремятся к нулю.
Частичные суммы знакочередующегося ряда меньше первого члена ряда
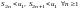 .
Члены ряда стремятся к нулю
.
Члены ряда стремятся к нулю
 ,
поэтому сумма ряда не может превосходить
первого члена ряда
,
поэтому сумма ряда не может превосходить
первого члена ряда
 .
.
Билет 13.
1.Полный дифференциал функции нескольких переменных
Сумма первых двух слагаемых в выражении полного приращения z называется полным дифференциалом и записывается
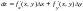 .В
частном случае, если функция z
= x,
то
.В
частном случае, если функция z
= x,
то
 ,
т. е.
,
т. е.
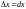 .
Аналогично при z
= y,
.
Аналогично при z
= y,
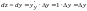 ,
т. е.
,
т. е.
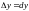 .Учитывая
это, полный дифференциал запишем в
виде
.Учитывая
это, полный дифференциал запишем в
виде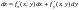 или
или
 .
.
Следовательно,
полное приращение функции
 равняется сумме полного дифференциала
и бесконечно малой величины более
высокого порядка малости по сравнению
с
равняется сумме полного дифференциала
и бесконечно малой величины более
высокого порядка малости по сравнению
с
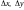 :
: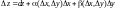 .
.
Найдем
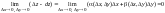 ,т.
е. полный дифференциал функции отличается
от полного приращения на бесконечно
малую функцию более высокого порядка
малости по сравнению с x,
y.
Поэтому полный дифференциал называют
главной линейной частью полного
приращения функции.
,т.
е. полный дифференциал функции отличается
от полного приращения на бесконечно
малую функцию более высокого порядка
малости по сравнению с x,
y.
Поэтому полный дифференциал называют
главной линейной частью полного
приращения функции.
Определение полного дифференциала функции нескольких переменных. Полным дифференциалом функции нескольких переменных называется бесконечно малая функция прямо пропорциональная бесконечно малым приращениям независимых переменных и отличающаяся от полного приращения функции на бесконечно малую функцию более высокого порядка малости по сравнению бесконечно малыми приращениями независимых переменных.
2.
Теорема
о существовании первообразной функции.
Для любой непрерывной функции существует
бесконечное множество первообразных
функций, отличающихся друг от друга на
постоянную величину. Д о к а з а т е л ь
с т в о. 1. Покажем, что для функции
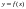 существует первообразная функция
существует первообразная функция
 ,
являющаяся площадью криволинейной
трапеции с переменной граничной прямой
(рис. 56).
,
являющаяся площадью криволинейной
трапеции с переменной граничной прямой
(рис. 56).
П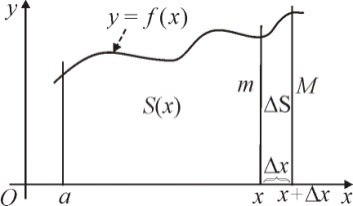 усть
правая граничная прямая изменяет
положение от х
до
усть
правая граничная прямая изменяет
положение от х
до
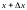 .
На этом отрезке
.
На этом отрезке
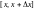 непрерывная функция
непрерывная функция
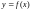 достигает своего наибольшего М
и наименьшего m
значений
достигает своего наибольшего М
и наименьшего m
значений ,
,
 .Очевидно,
значение площади элементарной
криволинейной трапеции
.Очевидно,
значение площади элементарной
криволинейной трапеции
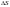 на отрезке
на отрезке
 удовлетворяет неравенству
удовлетворяет неравенству
 .
Поделим это неравенство на
.
Поделим это неравенство на
 ,
получим
,
получим
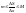 .
При
.
При
 наибольшее и наименьшее значения функции
на этом отрезке стремятся к одной и той
же величине
наибольшее и наименьшее значения функции
на этом отрезке стремятся к одной и той
же величине
 ,
,
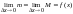 .
.
По
теореме о промежуточной функции
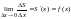 ,
т. е.
,
т. е.
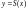 является первообразной для функции
является первообразной для функции
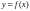 .
.
2.
Покажем, что для данной функции существует
бесконечное множество первообразных
функций. Действительно, если к данной
функции прибавить любую постоянную
величину, то ее производная не изменится ,
,
 .
.
3.
Покажем также, что любые две первообразные
функции отличаются друг от друга на
постоянную величину. Пусть
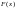 и
и
 первообразные функции для
первообразные функции для
 .
Тогда
.
Тогда
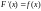 и
и
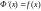 .
Найдем их разность, получим
.
Найдем их разность, получим
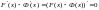 .
Если производная функции равна нулю,
то функция является постоянной.
Следовательно,
.
Если производная функции равна нулю,
то функция является постоянной.
Следовательно,
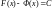 ,
где
,
где
 ,
и
,
и
 .
.
