Решение матричной игры в чистых стратегиях

Р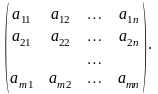 ассмотрим матричную игру с игроками P₁ и P₂ и платежной матрицей

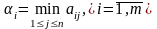П редполагая поведение игрока P₁ крайне осмысленным, необходимо считать, что игрок P₂ сыграет наилучшим для себя образом и на выбор игроком P₁ стратегии X_i выберет ту стратегию Y_j, при которой выигрыш игрока P₁ окажется минимальным. Обозначим минимальный среди выигрышей через α_i.

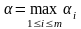Продолжая действовать разумно, игрок P₁ должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число α_i максимально.

Обозначим: , тогда . Число α называется нижней ценой игры в чистых стратегиях, а стратегия X_i0, которая максимизирует показатель эффективности α_i называется максиминной стратегией игрока P₁.

Н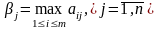 о так как игрок P₂ предполагает, что игрок P₁ играет наилучшим для себя образом, то выигрышем игрока P₁ будет максимальное из этих чисел, обозначим β_j:

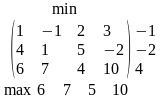
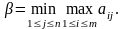
Т 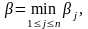аким образом, для любой стратегии Y_j игрока P₂ наибольший его проигрыш равен β_j. В интересах игрока P₂ выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел β_j обозначим β: тогда Число β называется верхней ценой игры в чистых стратегиях, а стратегия Y_j0, которая минимизирует показатель неэффективности β_j называется минимаксной стратегией игрока P₂.

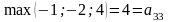
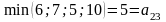
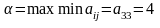
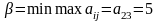-нижняя цена игры

-верхняя цена игры

X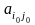 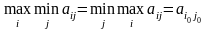₃ - максиминная стратегия, Y₃ - минимаксная стратегия

Е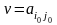 сли , то элемент называется седловым элементом матрицы А. Если платежная матрица A имеет седловой элемент , то матричная игра имеет решение в чистых стратегиях, при этом оптимальной стратегий первого игрока является X_i0 чистая стратегия, а для второго – Y_j0 чистая стратегия, а цена игры .

Р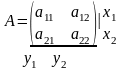 ешение матричной игры 2´2 в смешанных стратегиях

Решить игру с платежной матрицей

Е сли X*=(x₁; x₂) – оптимальная стратегия первого игрока, то по определению решения матричной игры

Е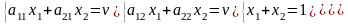 сли игра с нулевой суммой, то

Е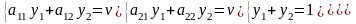 сли Y*=(y₁; y₂) – оптимальная стратегия второго игрока Если игра с нулевой суммой, то

Решение игр с платежной матрицей 2´n

Алгоритм:

1) Через концы горизонтального отрезка [0; 1] провести два перпендикуляра к нему: левый и правый. Каждой точке отрезка [0; 1] будем ставить некоторую смешанную стратегию (x; 1-x).

2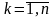 ) На левом перпендикуляре от точки 0 отложить элементы (a₁₁, …, a_1n). На правом перпендикуляре от точки 1 отложить элементы (a₂₁, …, a_2n).

3) Соединить отрезками элементы a_1k и a_2k ( ).

4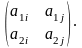 ) Выделить нижнюю огибающую всех построенных отрезков, и найти максимальную точку (точки). Пусть точка является пересечением отрезков [a_1i; a_2i] и [a_1j; a_2j]. Тогда оптимальную стратегию можно найти при помощи матрицы

В матрицах mx2 тоже самое, только берётся верхняя огибающая и минимальная точка.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Моделирование – метод исследования систем на основе переноса изучаемых свойств системы на объекты другой природы.

Процесс моделирования – построение модели и исследование характеристик системы с целью прогнозирования поведения системы при различных режимах

Выделяют 4 типа моделей:

• Физические (глобус)

• Электрические (построение цепей - аналоговые машины)

• Ситуационные (деловые игры)

• Математические

Работа над любой математической моделью начинается со сбора и анализа фактического материала. Определяются цели моделирования. Выделяются главные черты изучаемого объекта или явления и вводятся формализованные характеристики и правила работы с ними.

Модель – такой материальный или мысленно представленный объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение даёт новые знания об объекте оригинале.

Свойства модели

• Эффективность(насколько правильным было создание и использование модели для достижения поставленной цели);

• Универсальность(возможность её применения в других задачах и для достижения других целей);

• Устойчивость(означает её правильную работу в изменяющихся внешних условиях и экстренных ситуациях);

• Содержательность(определяет количество функции модели);

• Адекватность(определяет соответствие модели поставленной задаче);

• Ограниченность(всегда отображает объект-оригинал не во всех его свойствах и функциях);

• Полнота(наличие сведений об объекте-оригинале, необходимых для достижения поставленной цели);

• Динамичность(определяет изменение модели с течением времени).

Этапы построения мат. Модели:

• Определение цели, т.e. чего хотят добиться, решая поставленную задачу.

• Определение пapaметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.

• Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.

• Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.

• Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.

• Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.e. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.

Основные принципы построения математической модели:

• Необходимо соизмерять точность и подробность модели, во-первых, с точностью тex исходных данных, которыми располагает исследователь, и, во-вторых, с теми результатами, которые требуется получить.

• Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.

• Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.

• Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой (сохранять свойства и структуру при этих воздействиях).

Мат модели:

Детерминированные:

• Линейные

• Нелинейные

• Графические

• Динамические

Стохастические:

• Модели стохастического программирования

• Модели теории случайных процессов

• Модели теории массового обслуживания

Модели с элементами неопределённости:

• Модели теории игр

• Имитационные

СЛУ

Система m линейных уравнений с n неизвестными имеет вид:

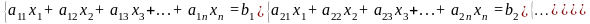. (1)

Здесь x1, x2, ¼, xn – неизвестные величины, aij (i = 1,2, ¼, m; j =1, 2, ¼, n) – произвольные числа, называемые коэффициентами системы, b1, b2, ¼, bm –числа, называемые свободными членами.

Решением системы будем называть упорядоченный набор чисел x1, x2, ¼, xn, обращающий каждое уравнение системы в верное равенство.

Система, имеющая решение, называется совместной.

Если система имеет только одно решение, то она называется определенной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной).

Если система не имеет решений, то она называется несовместной.

Система, у которой все свободные члены равны нулю, (b1 = b2 =¼= bn = 0), называется однородной. Однородная система всегда совместна, так как набор из n нулей удовлетворяет любому уравнению такой системы.

Элементарные преобразования над СЛУ:

1) вычеркивание уравнений вида ;

2) перестановка уравнений;

3) умножение любого уравнения на произвольное число, отличное от нуля;

4) сложение обеих частей одного из уравнений системы с соответствующими частями другого уравнения, умноженными на любое число, отличное от нуля.

Решаются методом Краммера или Гаусса

В Гауссе составляем расширенную матрицу и приводим к ступенчатому виду путём элементарных преобразований, потом переходим к эквивалентной системе и из неё находим все неизвестные

В Краммере составляем матрицу, находим множитель Δ, потом Δ₁, Δ₂ итд подставляя в матрицу столбец свободных членов в соответствующее место. Далее находим ответ воспользовавшись формулами Краммера: x₁= Δ₁/ Δ , x₂= Δ₂/ Δ итд.