
Нелинейное программирование
В общем виде задача нелинейного программирования формулируется следующим образом:
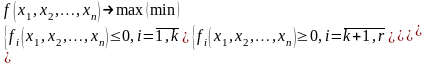
(1)
где fj, f – заданные функции от n переменных.
О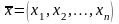 бозначим:
D – множество решений
системы ограничений задачи нелинейного
программирования (1); вектор
.
бозначим:
D – множество решений
системы ограничений задачи нелинейного
программирования (1); вектор
.
Р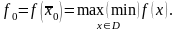
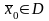 ешением
задачи нелинейного программирования
(1) называется вектор и число f0
такие, что
ешением
задачи нелинейного программирования
(1) называется вектор и число f0
такие, что
В зависимости от вида целевой функции и ограничений существуют несколько методов решения задач нелинейного программирования.
Графический метод . Алгоритм:
1) На плоскости построить область D допустимых решений системы ограничений задачи.
2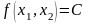 )
Если D = Æ,
то задача не имеет решения.
)
Если D = Æ,
то задача не имеет решения.
3) Если D ¹ Æ, то построить линию уровня функции , где С – константа.
4 ) Определить направление возрастания (при максимизации) или убывания (при минимизации) функции f.
5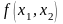
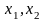 )
Найти точку области допустимых решений
D, через которую
проходит линия уровня с
наибольшим (при максимизации), наименьшим
(при минимизации) значением С или
установить неограниченность функции
f на области D.
)
Найти точку области допустимых решений
D, через которую
проходит линия уровня с
наибольшим (при максимизации), наименьшим
(при минимизации) значением С или
установить неограниченность функции
f на области D.
6) Определить значения найденной точки и значение
Классический метод (способ сведения задачи к одной переменной ) :
Р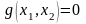
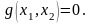 ассматривается
задача нахождения точек экстремума
функции при ограничении
ассматривается
задача нахождения точек экстремума
функции при ограничении
Е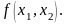
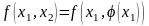
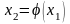 сли
уравнение можно разрешить
относительно одной переменной, например,
выразить x2 через
x1 : , то
полученное выражение можно подставить
в функцию f. Тогда
получим , т.
е. функцию одной переменной. Ее экстремум
и будет экстремумом функции
сли
уравнение можно разрешить
относительно одной переменной, например,
выразить x2 через
x1 : , то
полученное выражение можно подставить
в функцию f. Тогда
получим , т.
е. функцию одной переменной. Ее экстремум
и будет экстремумом функции
Метод множителей Лагранжа

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Метод динамического программирования позволяет находить оптимальное решение в ситуациях, когда имеется некоторое количество различных вариантов поведения, приносящих различные результаты, среди которых необходимо выбрать наилучший.
Задача об инвестировании предприятия
Требуется вложить имеющиеся a единиц средств в n предприятий, прибыль от которых в зависимости от количества x вложенных средств определяется таблицей:
x |
g1 |
g2 |
… |
gn |
x1 |
g1(x1) |
g2(x1) |
… |
gn(x1) |
x2 |
g1(x2) |
g2(x2) |
… |
gn (x2) |
… |
… |
… |
… |
… |
xm |
g1(xm) |
g2(xm) |
… |
gn(xm) |
(gi(xj)- прибыль i-ого предприятия при вложении в него xj средств), так, чтобы суммарная прибыль со всех предприятий была максимальна.
Разобьем процесс оптимизации на n шагов, и будем на k-ом шаге оптимизировать инвестирование только предприятий с k-ого по n-ое. Но т.к. с 1-го по (k-1)-ое предприятие также вкладываются некоторые средства, то на инвестирование предприятий с k-ого по n-ое остаются не все средства, а некоторая сумма ck£a. Эта величина и будет являться переменной состояния.
В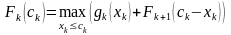 еличина
xk
средств, вкладываемых в k-ое
предприятие называется переменной
управления на k-ом
шаге. Максимально возможную прибыль,
которую можно получить с предприятий
с k-ого по n-ое
при условии, что на их инвестировании
осталось ck
средств определяется функцией
Беллмана:
еличина
xk
средств, вкладываемых в k-ое
предприятие называется переменной
управления на k-ом
шаге. Максимально возможную прибыль,
которую можно получить с предприятий
с k-ого по n-ое
при условии, что на их инвестировании
осталось ck
средств определяется функцией
Беллмана:
Н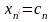
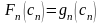 а
первом этапе решения задачи, который
называется условной оптимизацией
при k=n
функция Беллмана представляет собой
прибыль только с n-ого
предприятия, при этом на его инвестирование
может остаться ck
средств, 0£ck£a.
Очевидно, чтобы получить максимум
прибыли с этого последнего предприятия,
надо вложить в него все эти средства,
т.е. это максимальное
значение достигается при некотором
значении .
а
первом этапе решения задачи, который
называется условной оптимизацией
при k=n
функция Беллмана представляет собой
прибыль только с n-ого
предприятия, при этом на его инвестирование
может остаться ck
средств, 0£ck£a.
Очевидно, чтобы получить максимум
прибыли с этого последнего предприятия,
надо вложить в него все эти средства,
т.е. это максимальное
значение достигается при некотором
значении .
М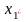 аксимально
возможная прибыль, которая может быть
получена с предприятий k-ого
по n-ое предприятие
будет равна
аксимально
возможная прибыль, которая может быть
получена с предприятий k-ого
по n-ое предприятие
будет равна
Б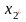
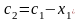 езусловная
оптимизация.
Зная оптимальное управление
на первом шаге , можно найти состояние
, а значит и .
езусловная
оптимизация.
Зная оптимальное управление
на первом шаге , можно найти состояние
, а значит и .
Поступая аналогичным образом до n-ого шага, получим оптимальный план инвестирования предприятий.
