4. Понятие о теории Гамильтона - Якоби

В теории ГамильтонаЯкоби действие задается как функция координат и времени. Чтобы величину (1.2) превратить из функционала в функцию, можно рассмотреть ее для «истинных» траекторий, для которых выполняются уравнения Лагранжа (1.8) или уравнения Гамильтона (44), считая верхний предел интегрирования переменным. Иными словами, рассмотрим интеграл действия (1.2) для «истинных» траекторий в конфигурационном пространстве, имеющих общее начало q(t₁) момент времени t₁ и проходящих через различные положения в момент времени t₂, которые будем просто обозначать буквой t.

При рассмотрении бесконечно малой вариации действия при переходе от одной траектории к другой можно воспользоваться общим выражением (1.5), где теперь нужно будет считать верхний предел интегрирования переменным, значение вариации q на верхнем пределе следует считать переменным, а на нижнем – положить равным нулю, а также следует учесть, что выполняются уравнения движения (1.8):

.        

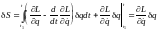Отсюда в силу (1.8) имеем

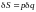.                                                                 (83)

Отсюда видно, что для действия как функции координат

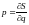.                                                                    (84)

Аналогично можно задавать действие как явную функцию времени, рассматривая траектории, проходящие в заданный момент времени t₁ через общую точку q₁, а в различные моменты времени t проходящие через одну и ту же точку q₂. Выражение для частной производной действия по времени проще всего получить, воспользовавшись (84) и рассматривая полную производную действия по времени как функции координат и времени:

.      

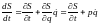Из (1.2) при переменном верхнем пределе следует, что dS/dt = L. Поэтому с учетом определения функции Гамильтона (38)

.

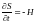Рассматривая здесь H как функцию времени, обобщенных координат и обобщенных импульсов, выраженных в виде частных производных действия по обобщенным координатам приходим к уравнению Гамильтона - Якоби

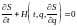.                                                   (85)

Уравнение (85) может рассматриваться как основное уравнение механики, в котором действие как функция координат и времени выступает в качестве основной характеристики механической системы. Уравнение Шредингера, являющееся основным уравнением квантовой механики, в пределе классической механики сводится к уравнению (85). Уравнение вида (85) встречается также и в геометрической оптике (подробнее об аналогии между механикой и геометрической оптикой см. [1]).

Литература

1. Синг Дж. Классическая динамика. М.: Наука, 1963.

2. Арнольд В.И. Математические методы классической механики. М.: Наука, 1979.

3. Терлецкий Я.П. Теоретическая механика. М.: изд-во УДН, 1987.

4. Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1973.

Приложение а. Выражение координат частиц системы материальных точек через координаты Якоби

Координаты Якоби, являющиеся коллективными переменными, описывающими положение системы материальных точек, определяются соотношениями (16), которые здесь воспроизведем в следующей собирательной форме

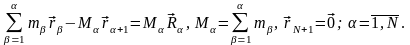                         (А.1)

Этой системе можно придать следующий матричный вид (M₁ = m₁):

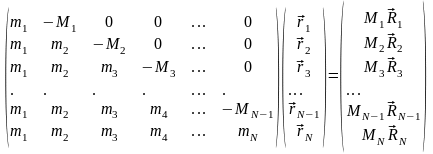.                     (А.1)

Матрица системы (А.1) может быть упрощена способом, являющимся частью метода Гаусса. Для этого последовательно вычтем первое уравнение из всех остальных уравнений системы, затем в получившейся системе второе уравнение вычтем последовательно из третьего, четвертого, и т.д. уравнений. Продолжая процесс до этапа, на котором предпоследняя строчка будет вычтена из последней, в конечном счете, преобразуем систему (А.1) к виду

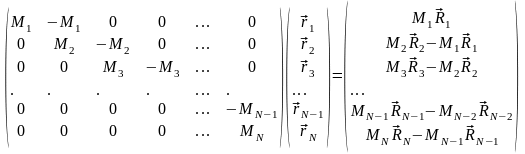.           (А.2)

Матрица, обратная к матрице системы (А.2), может быть легко вычислена (проверьте на примерах N = 2,3,4), что позволяет записать решение системы (А.1) в следующем матричном виде:

.

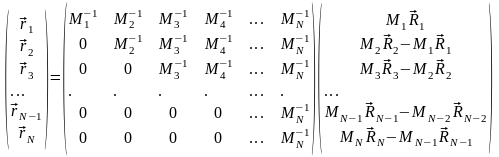После перемножения матрицы на вектор-столбец, стоящий слева, получаем:

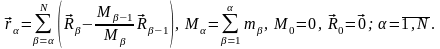
1 Например, для описания вращательного движения удобно взять угол поворота радиус-вектора точки вокруг некоторой оси.

1 В такой форме записи (иногда называемой прямой формой записи в отличие от индексной формы записи, представленной в левой части второго равенства (1.3)) можно вести все вычисления как будто бы с одной переменной, а получаемые результаты оказываются справедливыми и для многих переменных.

1 Такие связи еще называют неосвобождающими или двусторонними. В общем случае можно рассматривать связи, содержащие производные координат произвольного порядка, но с помощью уравнений движения все старшие производные можно выразить через производные меньшего порядка. Обычно в механике рассматриваются уравнения движения не выше второго порядка. Поэтому достаточно рассматривать условия связи вида (16).

2 Неголономные связи иногда называют кинематическими связями в противоположность геометрическим, или голономным связям.