
Решение
Корни
данного уравнения должны удовлетворять
условию 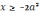 (условия существования квадратного
коря из выражения
(условия существования квадратного
коря из выражения  ).
Заметим, что
).
Заметим, что 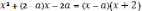 .
Тогда
.
Тогда
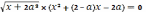
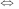
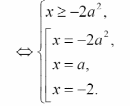
Следовательно,
корнями уравнения могут быть числа
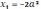 ,
,
 и
и  .
По условию задачи требуется найти
значение параметра а, при которых
уравнение имеет ровно два различных
корня. Для отбора искомых значений
параметра на плоскости Oax
построим графики функций
.
По условию задачи требуется найти
значение параметра а, при которых
уравнение имеет ровно два различных
корня. Для отбора искомых значений
параметра на плоскости Oax
построим графики функций 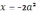 ,
,
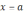 и
и 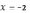 (см. рис.2). Каждая прямая при a
= const
параллельна оси Ox
и пересекает каждый из построенных
графиков, и ордината точки пересечения
дает значения корня исходного уравнения
при условии, что
(см. рис.2). Каждая прямая при a
= const
параллельна оси Ox
и пересекает каждый из построенных
графиков, и ордината точки пересечения
дает значения корня исходного уравнения
при условии, что 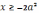 .
Точки (a,
x),координаты
которых удовлетворяют последнему
неравенству, расположены на плоскости
Oax
в выделенной фоном области.
.
Точки (a,
x),координаты
которых удовлетворяют последнему
неравенству, расположены на плоскости
Oax
в выделенной фоном области.
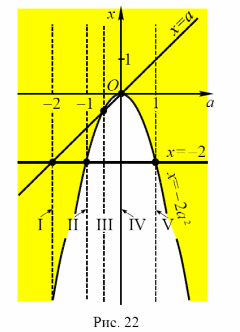

Имеется пять критических положений этих прямых:
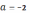 ,
2)
,
2) 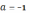 ,
3)
,
3) 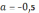 ,
4)
,
4) 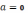 ,
5)
,
5) 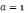 .
.
В этих случаях они проходят через точки пересечения графиков. Точки – 2, - 1, - 0,5, 0 и 1 разбивают числовую прямую Oa на шесть промежутков. Рассмотрим каждый из них:
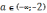 и (2)
и (2) 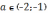 .
На этих промежутках уравнение имеет
три корня.
.
На этих промежутках уравнение имеет
три корня.
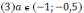 .
Уравнение имеет два корня ( график
функции
расположен
ниже графика функии
).
.
Уравнение имеет два корня ( график
функции
расположен
ниже графика функии
).
(4) 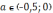 .
Уравнение имеет один корень, так как
графики функций
и
– ниже графика функции
.
.
Уравнение имеет один корень, так как
графики функций
и
– ниже графика функции
.
(5) 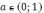 .Уравнение
имеет два корня ( график функции
- ниже графика функции
.Уравнение
имеет два корня ( график функции
- ниже графика функции 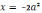 ).
).
(9)  .
Уравнение имеет три корня.
.
Уравнение имеет три корня.
Соответственно при каждом из значений , или уравнение имеет два корня.
Ответ: 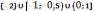 .
.
Пример 4:
Определить
значение параметра a,
при которых уравнение
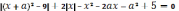 будет иметь
наибольшее число корней.
будет иметь
наибольшее число корней.
Решение
Приведем уравнение
к следующему виду 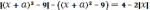 .
(*)
.
(*)
Рассмотрим два случая.
Если
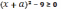 ,
то уравнение будет иметь вид . Отсюда
,
то уравнение будет иметь вид . Отсюда
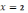 и
.
Для того, чтобы найденные значения
и
.
Для того, чтобы найденные значения 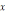 являлись решениями уравнения (*), должны
выполняться условия:
являлись решениями уравнения (*), должны
выполняться условия:
Если
,
то 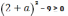
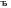
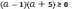
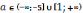 ;
;
Если
,
то 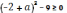
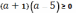
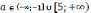 .
.
Если
 ,
то уравнение будет иметь вид
,
то уравнение будет иметь вид 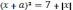 .
.
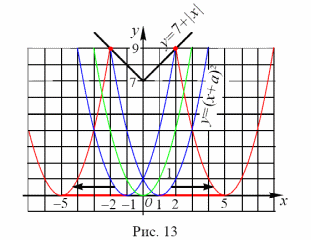

На рис.3
представлены графики функций 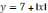 ,
стоящей в правой части последнего
уравнения, и графики функций
,
стоящей в правой части последнего
уравнения, и графики функций 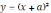 ,стоящей
в левой его части а.
Так как
должно выполняться условие
,стоящей
в левой его части а.
Так как
должно выполняться условие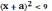 ,
то для существования корней должно быть
и
,
то для существования корней должно быть
и 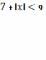 ,
т.е
,
т.е
 .
Это возможно только при
.
Это возможно только при 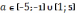 (см.рис.3)
(см.рис.3)
Причем решение
при этих значениях a
будет одно.
При 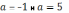 получается
;
при
получается
;
при 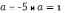 получим
;
при
получим
;
при 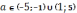 решением будет некоторое
решением будет некоторое 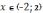 .
.
Сравнивая
полученные решения в первом и втором
случаях, имеем: при 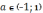 уравнение не имеет решений; при
уравнение не имеет решений; при 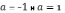 уравнение имеет одно решение; при
уравнение имеет одно решение; при 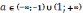 уравнение имеет два решения.
уравнение имеет два решения.
Ответ: При уравнение имеет два корня.
Пример 5:
Найдите все
значения а, при каждом из которых
уравнение
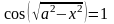 имеет ровно восемь различных решений.
имеет ровно восемь различных решений.
Решение:
1 Способ. ,
Построим графики
функций
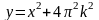 при
и
при
и
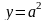 .
Графиком первой функции является
семейство парабол с вершинами,
расположенных на оси ОУ: у=0,
.
Графиком первой функции является
семейство парабол с вершинами,
расположенных на оси ОУ: у=0,

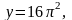
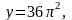
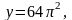
и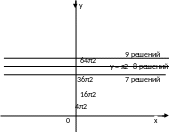 т.д. (в зависимости от k=0,1,2,3,4,…).
Графиком второй функции является
прямая, параллельная оси ОХ.
т.д. (в зависимости от k=0,1,2,3,4,…).
Графиком второй функции является
прямая, параллельная оси ОХ.
По графику определяем, что
ровно восемь
решений (точек пересечения) возможно в
том случае, если прямая
расположена выше прямой
но
ниже прямой
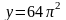 .
Следовательно,
.
Следовательно,

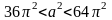 ,
,
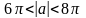 .
.
При
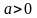
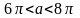 ,
,
при
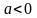
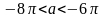 .
.
Ответ: ,
 Решение:
2 способ.
,
Заметим, что параметр а может принимать
как положительные, так и отрицательные
значения, но не равен нулю.
Решение:
2 способ.
,
Заметим, что параметр а может принимать
как положительные, так и отрицательные
значения, но не равен нулю.
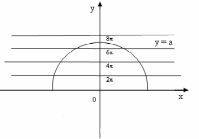
Построим
график функции
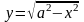 при у>0 , т.е.
при у>0 , т.е.
 или
или
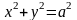 (полуокружность с центром в начале
координат) . Графиком второй функции
(полуокружность с центром в начале
координат) . Графиком второй функции
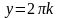 при
является
семейство прямых, параллельных оси ОХ,
проходящих через точки с ординатами
у=0,
при
является
семейство прямых, параллельных оси ОХ,
проходящих через точки с ординатами
у=0,
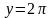 ,
,
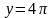 ,
,
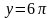 ,
,
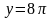 и т.д.
и т.д.
Рассмотрим полуокружность радиуса r=a. Если радиус , то полуокружность пересекает серию прямых ровно в восьми точках. Аналогично рассуждаем для случая а<0.
Ответ: ,
Пример
6:
Найдите все значения параметра a,
при котором уравнение
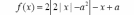 имеет
три различных корня.
имеет
три различных корня.
