16. Поведение траекторий в окрестности экватора сферы Пуанкаре (s2 p)

Рассматриваем систему вида:

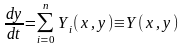, (1). Прямая z=0 на плоскостях 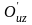и является бесконечно удаленной прямой (БУП) на проективной пл-ти (z,x,y). Является или нет эта прямая траекторией системы (1) зависит от этой системы.

Теорема: Для того чтобы у дифференциальной сис-мы(1) прямая z=0, была траекторией необходимо и достаточно чтобы эта система имела P–неособый тип.

Док–во: В самом деле, прямая z=0 не яв-ся траекторией систем

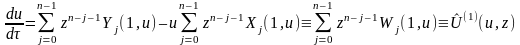
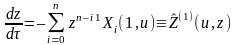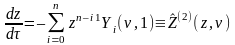
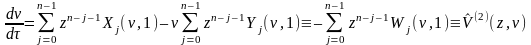(2) и , (3)

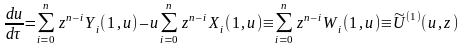
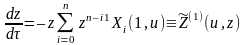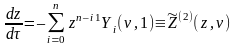
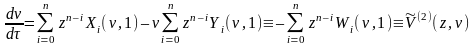но она является траекторией систем (4) и (5)

Это устанавливается по видам P–приведенных систем с учетом условий 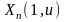≡0 на R (6) и 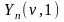≡0 на R (7) , 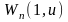≡0 на R (8) и 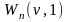≡0 на R (9)

Экватор S²P является образом БУП, поэтому поведение траекторий сис-мы (1) в окрестности экватора S²P будем изучать в зависимостиот ее P–типа. В первую очередь будем устанавливать, яв-ся или нет экватор траекторией сис-мы (1). Во вторую очередь, находим состояния равновесия (СР) сис-мы (1).

Для дальнейшего исследования будем учитывать следующие свойства траекторий в точках проективной ф. пл-ти (ПФП) системы (1).

Опр. Точку ПФП системы (1), которая не является СР, будем называть регулярной.

Бесконечно удаленные регулярные точки лежат на прямой z=0, их обозначают ∞– регулярные точки. На S²P бесконечно регулярной точке соответствует 2 антиподальные точки экватора, через каждую из которых проходит только одна траектория системы (1) на S²P.

Опр. Точку, в которой траектория системы (1) касается кривой γ, лежащей на фазовой плоскости (ФП), назовем контактной точкой кривой γ.

Свойство 1: Каждая точка кривой γ является контактной тогда и только тогда когда кривая γ является траекторией системы (1).

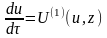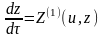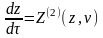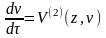Среди бесконечно удаленных точек (БУТ) будем выделять те, которые являются контактными точками прямой z=0 хотя бы одной из систем , (10) и , (11)

Эти точки называются экваториально–контактными (ЭК) точками системы (1). ЭК траекториями системы (1) называются траектории, которые на S²P касаются экватора.

Если ЭК точка является регулярной, то через нее на S²P проходит одна траектория, и она является ЭК траекторией.

Если ЭК точка является СР, то через нее может проходить несколько ЭК траекторий.

P–неособый тип

Система (1) имеет P–неособый тип тогда и только тогда когда выполняется условие W_n(x,y)≡xY_n(x,y)−yX_n(x,y)≡0 . В этом случае экватор является ЭК траекторией системы (1). Любая БУТ системы (1) является ЭК и через нее проходит траектория прямая z=0.Траектория системы (1) не имеет общих точек с экватором отличных от бесконечно удаленного состояния равновесия (БУ СР). У систем (4) и (5) находим СР, которые лежат на прямой z=0 и определяют характер. СР В_i(b_i,0) системы (4) лежат на концах прямой y=b_ix.

Свойство 2:Система (1) с P–неособым типом имеет БУ СР, лежащее на концах прямой y=bx, если и только если u=b является корнем уравнения W_n(1,u)=0.

СР вида C_i(0,c_i) системы (5) лежит на концах прямой x=c_iy.

Свойство 3: Система (1) с P–неособым типом имеет БУ СР, лежащее на концах прямой x=cy, если и только если v=c является корнем уравнения W_n(v,1)=0.

Свойство 4: Система (1) с P–неособым типом имеет БУ СР O˝, лежащее на концах прямой x=0, если и только если W_n(0,1)=0.

Если B_i(b_i,0), где b_i≠0 является СР системы (4), то C_i(0,c_i), c_i=1∕b_i будет СР системы (5) и наоборот, если C_i СР системы (5),то B_i(b_i,0), b_i=1∕c_i ,будет СР системы (4). Поэтому для исследования СР на экваторе S²P достаточно исследовать СР системы (4), которое расположено на прямой z=0 и определить является ли СР O˝ системы (5) или наоборот, исследовать СР системы (5) на прямой z=0 и определить является ли СР O′ системы (4).

При построении фазового портрета окружность круга Пуанкаре изображается сплошной линией.

P–особый тип

Система (1) имеет P–особый тип тогда и только тогда когда выполняется условие W_n(x,y)≡0, 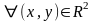. На S²P экватор не является траекторией системы (1). Через любую регулярную точку экватора проходит 1 траектория системы (1) отличная от экватора. Поведение траекторий в окрестности экватора определяется СР, лежащем на экваторе и регулярными ЭК точками.

СР системы (1), лежащее на экваторе является СР систем (2) и (3), которые лежат на прямой z=0.

Свойство 5: Система (1) с P–особым типом имеет БУ СР, лежащее на концах прямой y=bx, если и только если u=b является решением двух уравнений X_n(1,u)=0, W_n−1(1,u)=0.

Свойство 6: Система (1) с P–особым типом имеет БУ СР, лежащее на концах прямой x=cy, если и только если v=c является решением двух уравнений Y_n(v,1)=0, W_n−1(v,1)=0.

Свойство 7: Для того чтобы система (1) с P–особым типом имеет БУ СР O˝, лежащее на концах прямой x=0, необходимо и достаточно выполнение двух равенств Y_n(0,1)=0, W_n−1(0,1)=0.

Связь между СР B_i(b_i,0) системы (2) и СР C_i(0,c_i) системы (3) таково, как и в случае систем (4) и (5),поэтому исследование СР на экваторе, так же как и в случае P–неособым типом: вместо сист. (4) рассматриваем (2), а вместо (5) рассматриваем (3). На ряду с СР будем находить регулярные ЭК точки сист. (1).

Свойство 8: Система (1) с P–особым типом имеет регулярную ЭК точку B, расположенную на концах прямой y=bx, тогда и только тогда когда u=b является решением уравнения X_n(1,u)=0, а W_n−1(1,u)≠0. 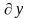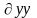При этом 1)если W_n−1(1,b) X_n(1,b)<0,то ЭК B–траектория в достаточно малой окрестности точки B, расположенной в полуплоскости x>0; 2) если W_n−1(1,b) X_n(1,b)>0,то ЭК B–траектория расположена в полуплоскости x<0; 3)если X_n(1,b)=0, W_n−1(1,b) X_n(1,b)≠0,то ЭК B–траектория расположена как в полуплоскости x<0, так и в полуплоскости x>0.

Свойство 9: Система (1) с P–особым типом имеет регулярную ЭК точку C, расположенную на концах прямой x=cy, тогда и только тогда когда v=c является решением уравнения Y_n(c,1)=0, а W_n−1(c,1)≠0. 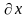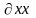При этом 1)если W_n−1(c,1) Y_n(c,1)<0,то ЭК C–траектория в достаточно малой окрестности точки C, расположенной в полуплоскости y<0; 2) если W_n−1(c,1) Y_n(c,1)>0,то ЭК C–траектория расположена в полуплоскости y>0; 3)если Y_n(c,1)=0, W_n−1(c,1) Y_n(c,1)≠0,то ЭК C–траектория расположена как в полуплоскости y<0, так и в полуплоскости y>0.

Свойство 10: Система (1) с P–особым типом имеет регулярную ЭК точку O˝, расположенную на концах прямой x=0, тогда и только тогда когда выполняется Y_n(0,1)=0, а W_n−1(0,1)≠0. При этом 1)если W_n−1(0,1) Y_n(0,1)<0,то ЭК O˝–траектория расположена в полуплоскости y<0; 2) если W_n−1(0,1) Y_n(0,1)>0,то ЭК O˝–траектория расположена в полуплоскости y>0; 3)если Y_n(0,1)=0, W_n−1(0,1) Y_n(0,1)≠0,то ЭК O˝ –траектория расположена как в полуплоскости y<0, так и в полуплоскости y>0.

Получаем для нахождения регулярных ЭК точек достаточно найти регулярные ЭК точки сист. (2), расположенные на прямой z=0 и проверить является ли регулярной ЭК точка O˝сист. (3) или наоборот, определить регулярные ЭЕ точки сист. (3), расположенные на z=0 и проверить является ли ЭК регулярная точка O′ системы (2).