1. Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.

Рассмотрим линейную динамическую систему

,

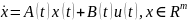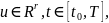
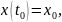с квадратичным функционалом качества управления

,

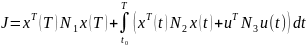. Гамильтониан системы . Необходимые условия оптимальности управления

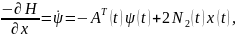
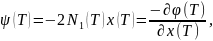
.Из последнего уравнения следует, что 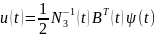. Подставляя это решение в предыдущее уравнение, получим краевую задачу , , 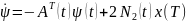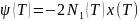. Обозначим 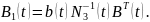Далее ищем вектор-функцию ψ(t) в виде 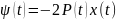, P(t) – симметричная матрица, которая подлежит определению. Продифференцируем обе части последнего равенства по t. Тогда получим

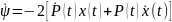. Заменяя производные 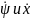в соответствии с исходными уравнениями для краевой задачи, получим

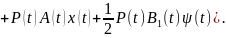Подставляя вместо ψ(t) величину -2P(t)x(t), получим уравнение для нахождения матрицы P(t).

,

).

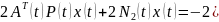
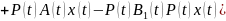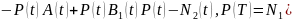Это уравнение матричного уравнения Риккати. Оно имеет единственное решение и позволяет оп-ределить оптимальное управление в виде . Оптимальное управление в линейно-квадратичной задаче связано с текущим состоянием системы линейным оператором. Зависимость означает, что для обеспечения оптимального управления, минимизирующего квадратичный функционал (то есть затраты энергии на управление), необходимо обеспечить пропорциональное изменению состояния, обратное по знаку воздействие на управляемый объект. Для получения оператора в явном виде надо найти решение уравнения Риккати, которое в явном виде получить сложно.

2. Управление ресурсами и задача линейного программирования. Примеры, геометрическая интерпретация.

Факторы, от которых зависит исход операции, делятся на две группы:

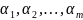• – набор факторов, которые известны заранее и на которые мы не можем влиять;

• – зависящие от нас факторы, которые, с учетом действующих ограничений, мы можем определять в процессе управления – выполнения операции.

Эффективность операции характеризуется числовым критерием или показателем W, который требуется обратить в максимум (или минимум)

,

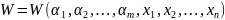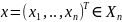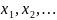, выбирая наборы при заданных 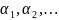, принадлежащие к области допустимых значений .

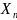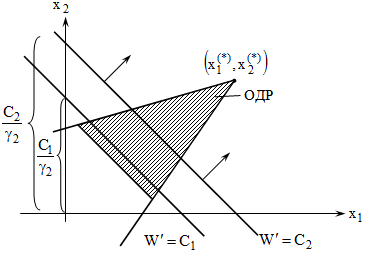
Геометрическая интерпретация ОЗЛП.

Пусть 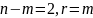. Тогда две из переменных, например 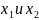, можно выбрать в качестве свободных, а остальные m сделать базисными и выразить их через свободные переменные. Получим 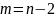уравнений вида

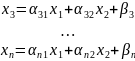(1)

Полученные уравнения определяют область допустимых решений (ОДР). 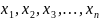должны быть неотрицательны. Из уравнений получим n прямых, включая и оси и 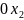. Каждая из них определяет допустимую область – полуплоскость, лежащую по одну сторону прямой и соответствующую условию .

Часть плоскости , принадлежащая полуплоскостям, образует область допустимых решений (ОДР). ОДР всегда образует выпуклый многоугольник. Может оказаться, что общей области неотрицательных решений нет. Тогда ОДР не существует. Для нахождения оптимального решения 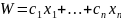также используем геометрическую интерпретацию для случая . Подставим выражения (1) для 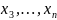в выражение для W и после приведения подобных членов получим 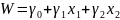, где 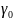– сво-бодный член, а – коэффициенты при . 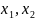Функция W достигает минимума при тех же значениях, что и 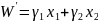. Для нахождения придадим W’ постоянное значение .

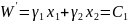
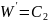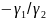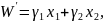
Другому значению соответствует прямая линия, параллельная первоначальной. Отсюда следует, что для нахождения решения необходимо построить основную прямую с угловым коэффициентом . и 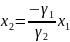и перемещать ее в направле-нии, для которого значение 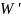убывает.

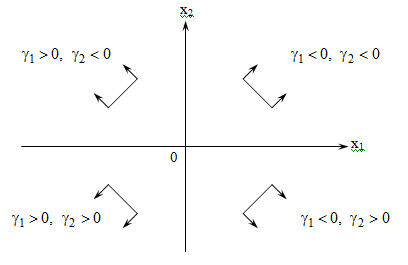
Очевидно, что при перемещении в указанных направлениях значение W достигает минимума в точке, являющейся крайней точкой ОДР. В этой точке 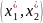, являющейся оптимальным решением, определяются значения и других переменных, а также достигаемое значение W

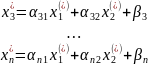
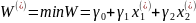. Закономерно-сти говорят нам о следующем.

1. Решение ОЗЛП, если оно существует, лежит на границе ОДР. ОЗЛП может не иметь решения, если в направлении движения с уменьшением W ОДР неограниченна.

2. Решение достигается в одной из вершин выпуклого многоугольника ОДР, каждая из которых отвечает некоторому «опорному» решению.

3. Две переменные для любой из вершин равны нулю. Из этого следует возможность нахождения оптимального решения на основе перебора всех вершин ОДР.

Контрольно-измерительный материал № 10