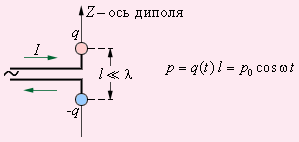Дифференциальная форма
Уравнения
Максвелла представляют собой в векторной
записи систему из четырёх уравнений,
сводящуюся в компонентном представлении
к восьми (два векторных уравнения
содержат по три компоненты каждое плюс
два скалярных[28])
линейных дифференциальных
уравнений в частных производных
первого порядка
для 12 компонент четырёх векторных
функций (![]() ):
):
Название |
СГС |
СИ |
Примерное словесное выражение |
Закон Гаусса |
|
|
Электрический заряд является источником электрической индукции. |
Закон Гаусса для магнитного поля |
|
|
Не существует магнитных зарядов.[~ 1] |
Закон индукции Фарадея |
|
|
Изменение магнитной индукции порождает вихревое электрическое поле.[~ 1] |
Теорема о циркуляции магнитного поля |
|
|
Электрический ток и изменение электрической индукции порождают вихревое магнитное поле |
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.
Введённые обозначения:
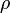 —
плотность
стороннего электрического
заряда
(в единицах СИ —
Кл/м³);
—
плотность
стороннего электрического
заряда
(в единицах СИ —
Кл/м³);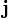 —
плотность
электрического тока
(плотность тока проводимости) (в единицах
СИ — А/м²);
в простейшем случае — случае тока,
порождаемого одним типом носителей
заряда,
она выражается просто как
—
плотность
электрического тока
(плотность тока проводимости) (в единицах
СИ — А/м²);
в простейшем случае — случае тока,
порождаемого одним типом носителей
заряда,
она выражается просто как
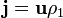 ,
где
,
где
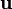 —
(средняя) скорость
движения этих носителей в окрестности
данной точки,
—
(средняя) скорость
движения этих носителей в окрестности
данной точки,
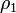 —
плотность заряда этого типа носителей
(она в общем случае не совпадает с
)[29];
в общем случае это выражение надо
усреднить по разным типам носителей;
—
плотность заряда этого типа носителей
(она в общем случае не совпадает с
)[29];
в общем случае это выражение надо
усреднить по разным типам носителей; —
скорость
света
в вакууме (299 792 458 м/с);
—
скорость
света
в вакууме (299 792 458 м/с);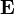 —
напряжённость
электрического поля
(в единицах СИ — В/м);
—
напряжённость
электрического поля
(в единицах СИ — В/м);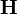 —
напряжённость
магнитного поля
(в единицах СИ — А/м);
—
напряжённость
магнитного поля
(в единицах СИ — А/м);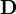 —
электрическая
индукция
(в единицах СИ — Кл/м²);
—
электрическая
индукция
(в единицах СИ — Кл/м²);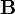 —
магнитная
индукция
(в единицах СИ — Тл
= Вб/м²
= кг•с−2•А−1);
—
магнитная
индукция
(в единицах СИ — Тл
= Вб/м²
= кг•с−2•А−1); —
дифференциальный
оператор
набла,
при этом:
—
дифференциальный
оператор
набла,
при этом:
![]() означает
ротор
вектора,
означает
ротор
вектора,
![]() означает
дивергенцию
вектора.
означает
дивергенцию
вектора.
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины , , , и и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
![]()
можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):
![]()
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:
![]()
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

6!!!
Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные ниже четыре уравнения:
1. Электрическое поле может быть как потенциальным (ЕQ), так и вихревым (ЕB), поэтому напряженность суммарного поля Е = ЕQ + ЕB. Так как циркуляция вектора ЕQ равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
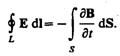
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
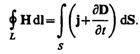
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D (см. (89.3)):
![]() (139.1)
(139.1)
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула (139.1) запишется в виде
![]()
4. Теорема Гаусса для поля В (см. (120.3)):
![]()
Итак, полная система уравнений Максвелла в интегральной форме:
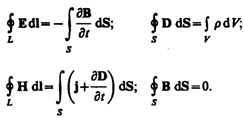
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
![]()
где 0 и 0 — соответственно электрическая и магнитная постоянные, и — соответственно диэлектрическая и магнитная проницаемости, — удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид
![]()
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
При помощи формул Остроградского — Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Название |
СГС |
СИ |
Примерное словесное выражение |
Закон Гаусса |
|
|
Поток
электрической индукции через замкнутую
поверхность
|
Закон Гаусса для магнитного поля |
|
|
Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют). |
Закон индукции Фарадея |
|
|
Изменение
потока
магнитной индукции,
проходящего через незамкнутую
поверхность
,
взятое с обратным знаком, пропорционально
циркуляции электрического поля на
замкнутом контуре
|
Теорема о циркуляции магнитного поля |
|
|
Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность , пропорциональны циркуляции магнитного поля на замкнутом контуре , который является границей поверхности . |
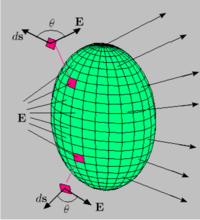
![]()
Поток электрического поля через замкнутую поверхность
Введённые обозначения:
— двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём , и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур ).
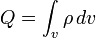 —
электрический
заряд,
заключённый в объёме
,
ограниченном поверхностью
(в
единицах СИ — Кл);
—
электрический
заряд,
заключённый в объёме
,
ограниченном поверхностью
(в
единицах СИ — Кл);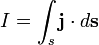 —
электрический
ток,
проходящий через поверхность
(в
единицах СИ — А).
—
электрический
ток,
проходящий через поверхность
(в
единицах СИ — А).
При
интегрировании по замкнутой поверхности
вектор элемента площади
![]() направлен
из объёма наружу. Ориентация
при
интегрировании по незамкнутой поверхности
определяется направлением правого
винта,
«вкручивающегося» при повороте в
направлении обхода контурного интеграла
по
направлен
из объёма наружу. Ориентация
при
интегрировании по незамкнутой поверхности
определяется направлением правого
винта,
«вкручивающегося» при повороте в
направлении обхода контурного интеграла
по
![]() .
.
Словесное
описание законов Максвелла, например,
закона Фарадея, несёт отпечаток традиции,
поскольку вначале при контролируемом
изменении магнитного потока регистрировалось
возникновение электрического поля
(точнее электродвижущей
силы).
В общем случае в уравнениях Максвелла
(как в дифференциальной, так и в
интегральной форме) векторные функции
![]() являются
равноправными неизвестными величинами,
определяемыми в результате решения
уравнений.
являются
равноправными неизвестными величинами,
определяемыми в результате решения
уравнений.
Таблица 2. Замкнутая система уравнений Максвелла.
Интегральная форма |
Дифференциальная форма |
|
|
|
|
|
|
|
|
Материальные уравнения |
|
|
|


8!!!!!!!
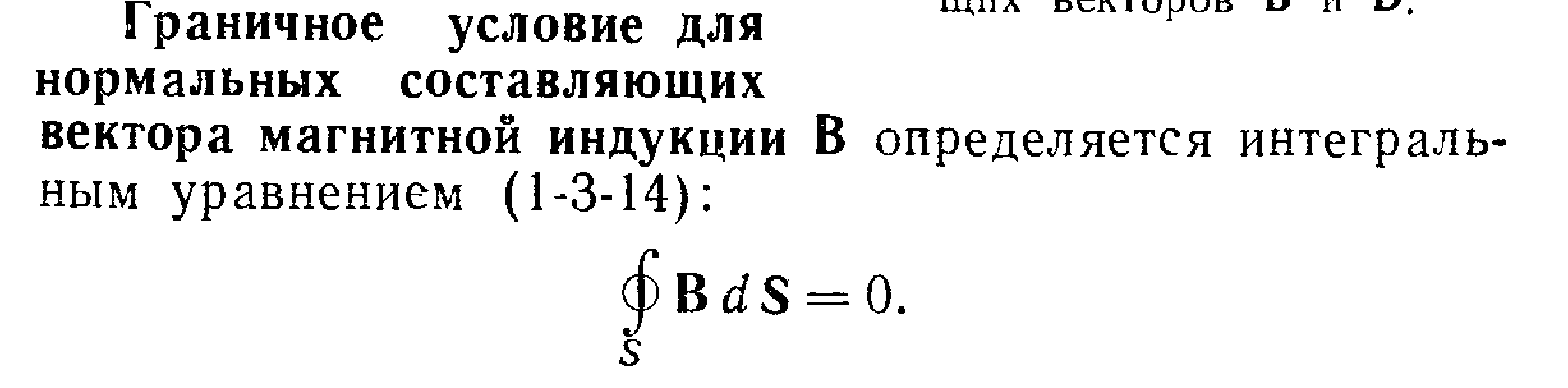
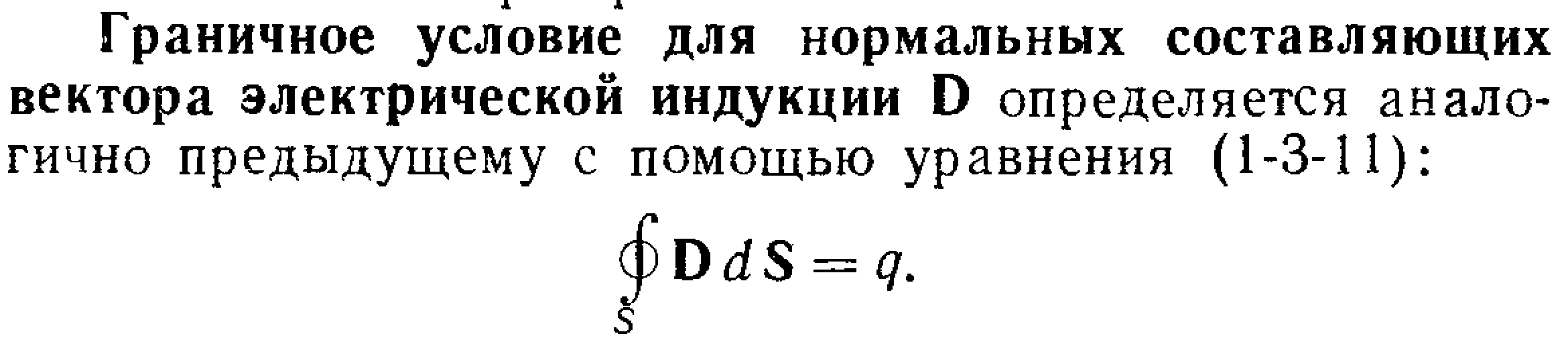
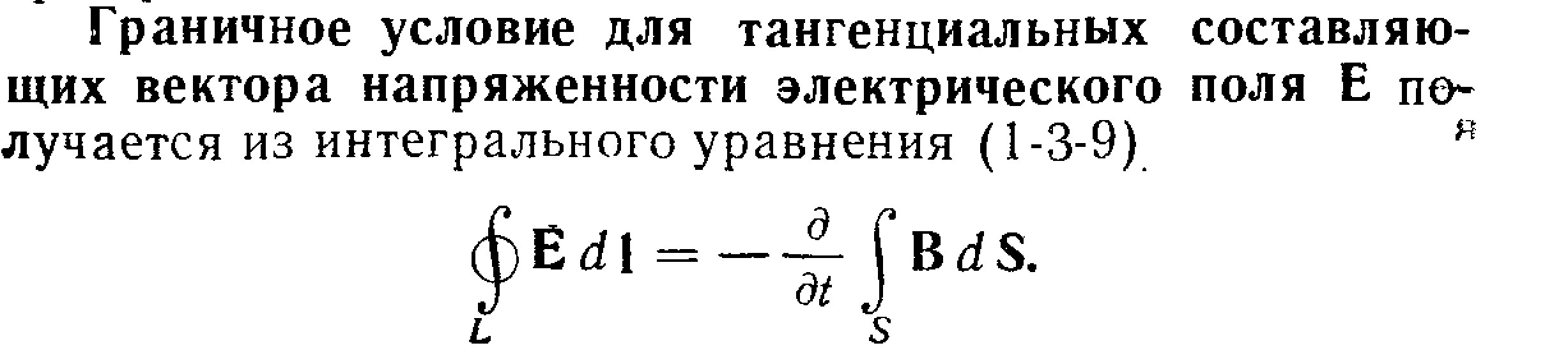
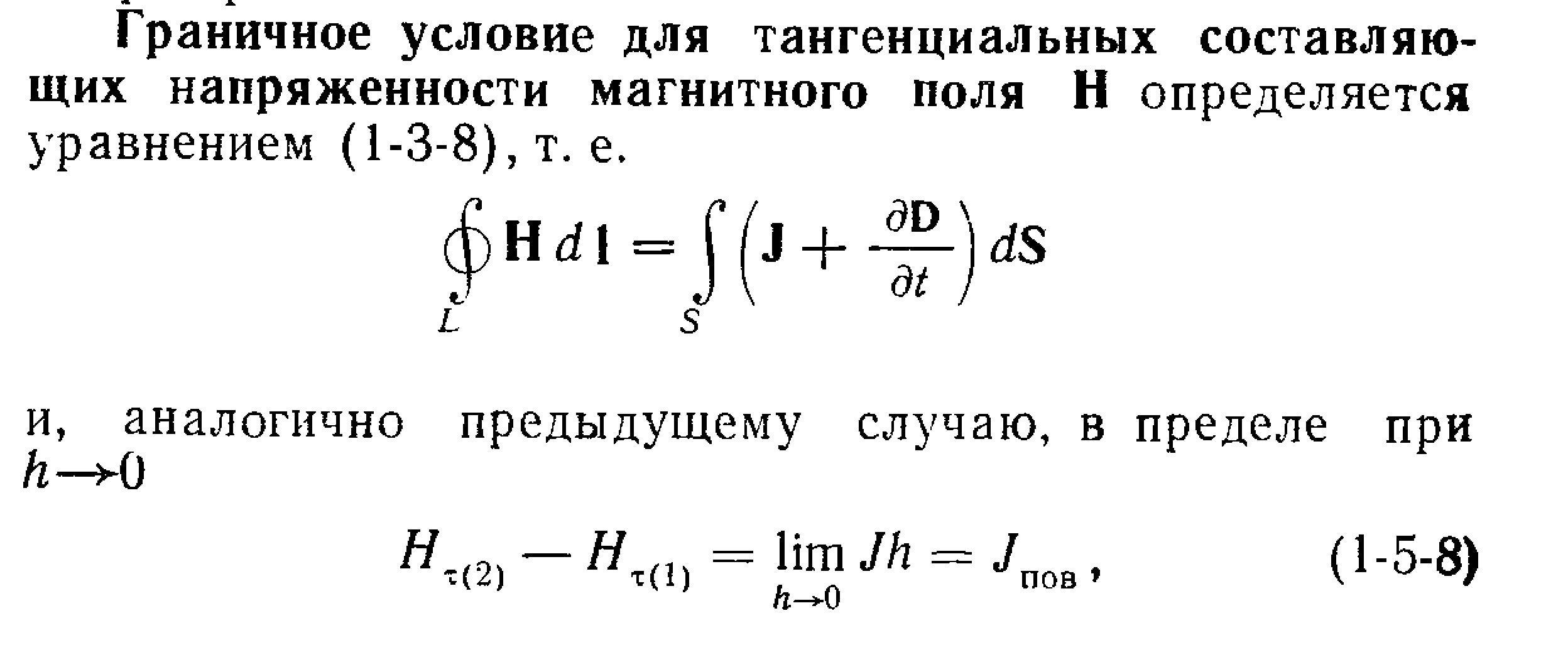
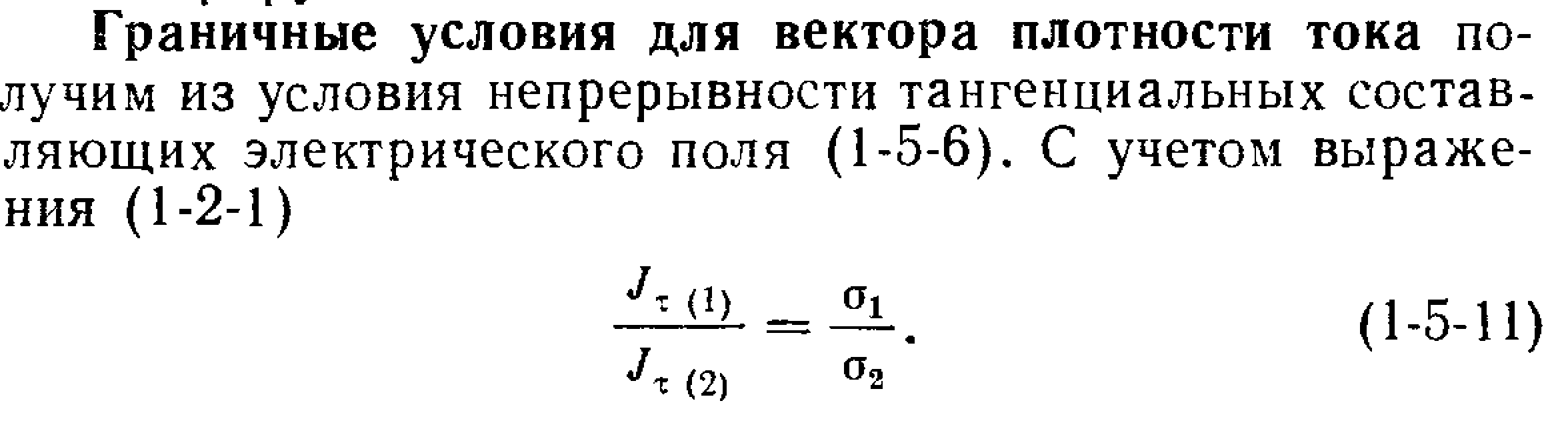
![]()
![]()

9!!!!!!
Теорема Пойнтинга (англ. Poynting's theorem) — теорема, описывающая закон сохранения энергии электромагнитного поля. Теорема была доказана в 1884 Джоном Генри Пойнтингом. Всё сводится к следующей формуле:
![]() ,
,
Где
S — вектор
Пойнтинга, J — плотность
тока и E — электрическое
поле. Плотность
энергии
![]() (
(![]() —
электрическая
постоянная,
—
электрическая
постоянная,
![]() —
магнитная
постоянная).
—
магнитная
постоянная).
![]()
Теорема Пойнтинга в интегральной форме:
![]() ,
,
где
![]() —
поверхность, ограничивающая объём
—
поверхность, ограничивающая объём
![]() .
.
В технической литературе теорема обычно записывается так ( — плотности энергии):
![]() ,
,
где
![]() —
плотность энергии электрического поля,
—
плотность энергии электрического поля,
![]() —
плотность энергии магнитного
поля и
—
плотность энергии магнитного
поля и
![]() —
мощность
джоулевых
потерь в единице объёма.
—
мощность
джоулевых
потерь в единице объёма.
10!!!!!!!
![]()
Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте
![]()
12!!!!!!
Соотношения Мэнли — Роу — энергетические соотношения, характеризующие взаимодействие колебаний или волн в нелинейных системах с сосредоточенными или распределёнными параметрами.
В общем виде соотношения Мэнли — Роу могут быть записаны следующим образом:
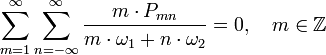
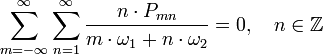
где
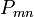 —
изменение
мощности на комбинационной частоте
—
изменение
мощности на комбинационной частоте
 ,
,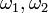 —
частоты
исходных колебаний (волн). Причём
отношение
—
частоты
исходных колебаний (волн). Причём
отношение
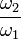 должно
быть иррационально, поскольку в противном
случае, возможно выразить все частоты
как гармоники одной фундаментальной
частоты.
должно
быть иррационально, поскольку в противном
случае, возможно выразить все частоты
как гармоники одной фундаментальной
частоты.
13!!!!!!!!

![]()
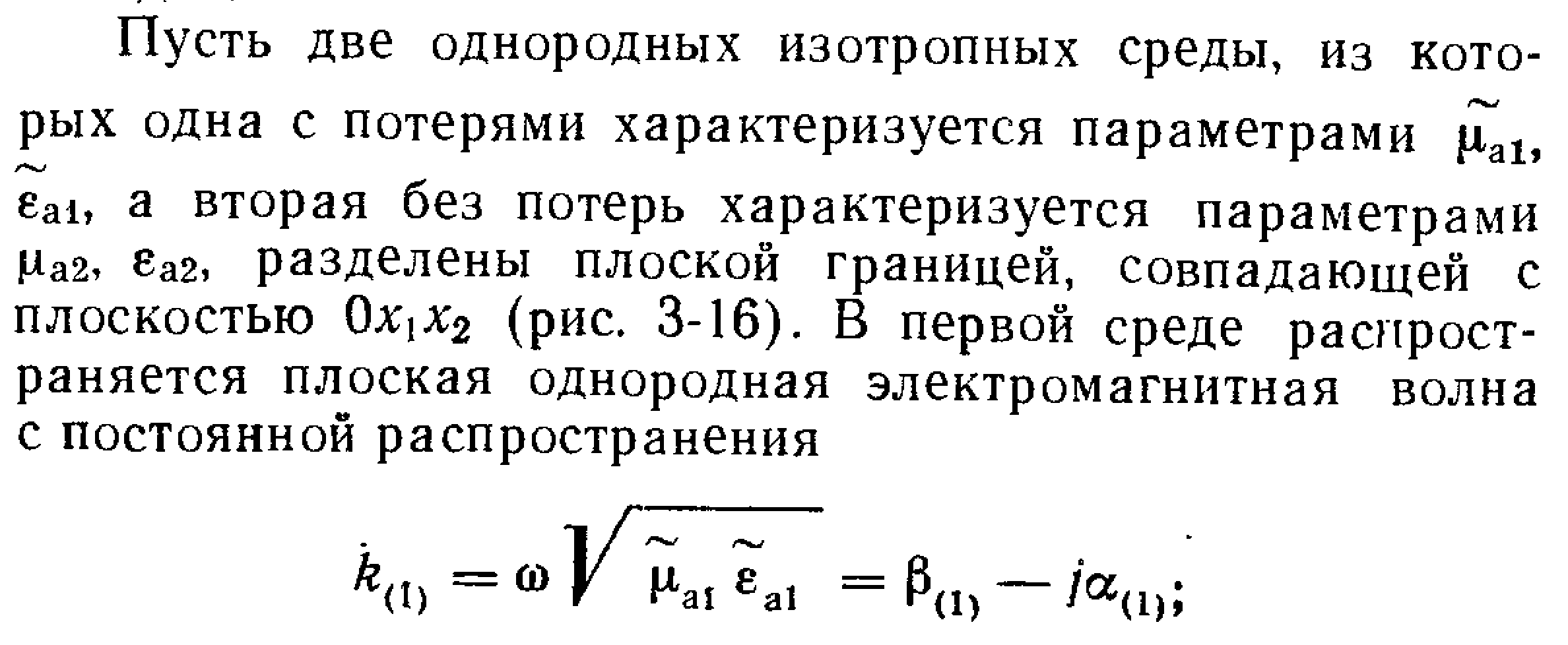

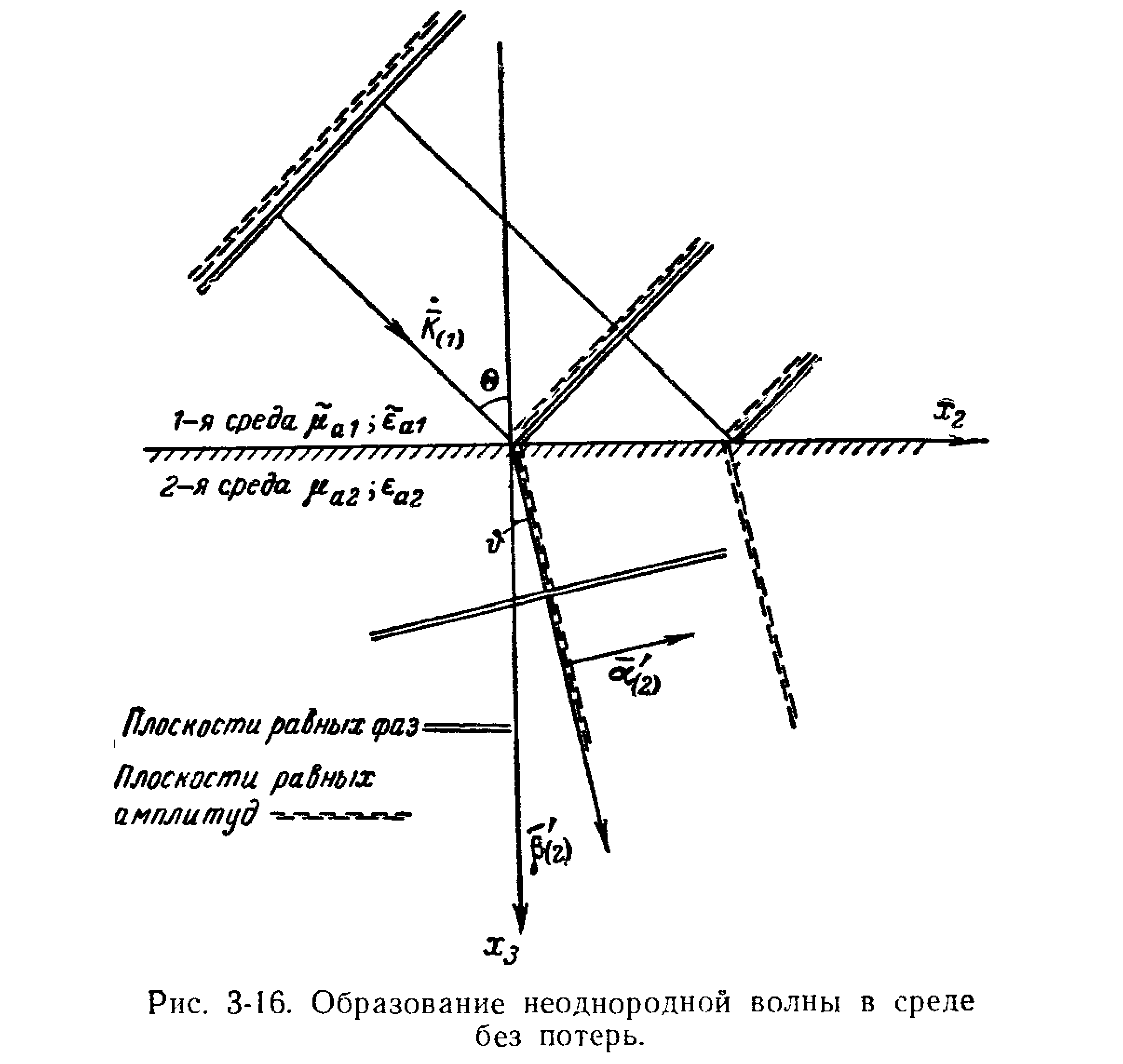



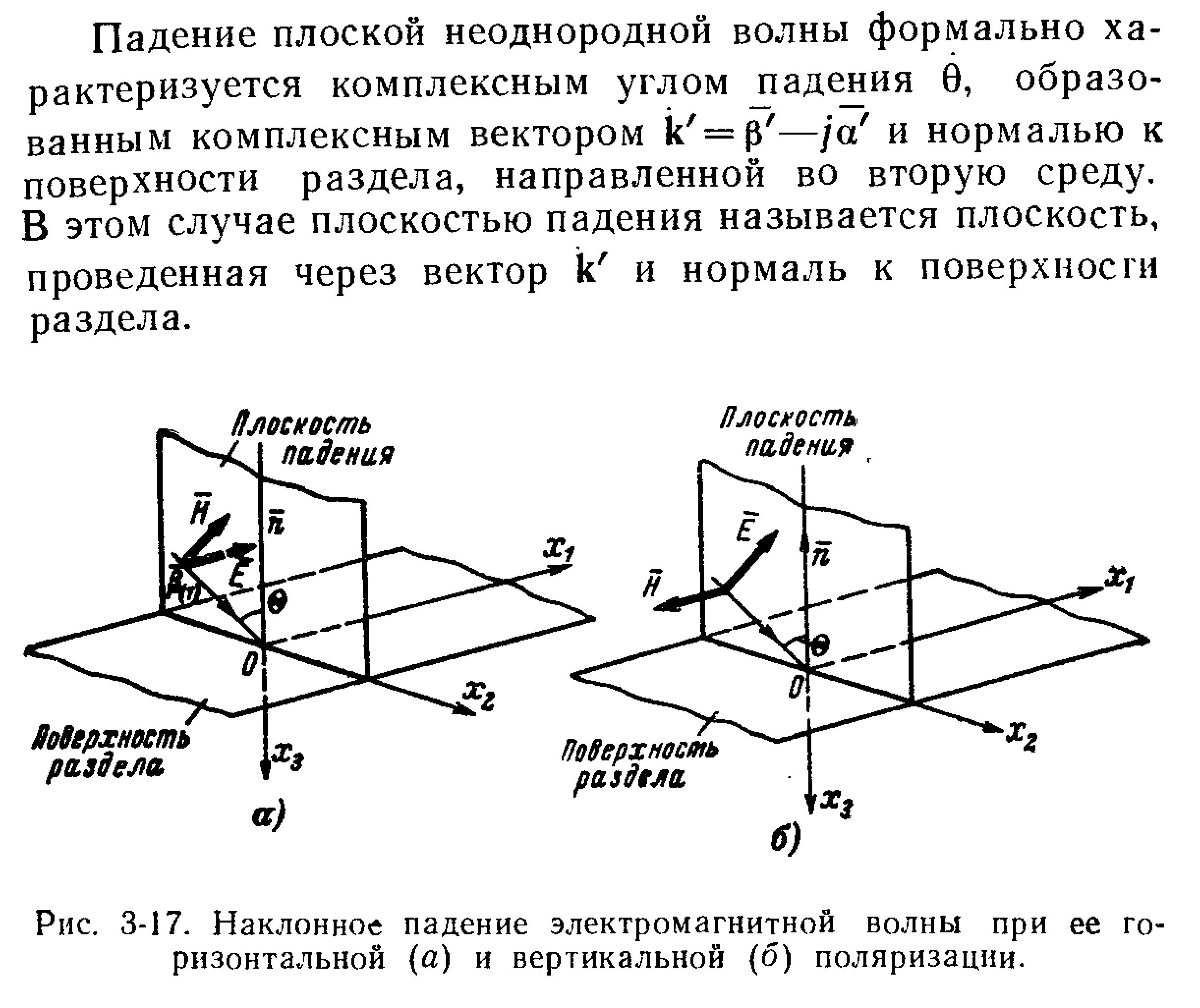
14!!!!!!
ГЕРЦА
ВЕКТОР - - потенциал эл--магн. поля, т.
е. вспомогат. ф-ция, через к-рую однозначно
выражаются напряжённости электрич.
![]() и
магн.
и
магн.
![]() полей.
Впервые введён Г. P. Герцем в 1888. Понятие
Г. в. можно использовать лишь для
однородных сред с изотропными
проницаемостями
полей.
Впервые введён Г. P. Герцем в 1888. Понятие
Г. в. можно использовать лишь для
однородных сред с изотропными
проницаемостями
![]() .
Различают электрич.
.
Различают электрич.
![]() и
магн.
и
магн.
![]() Г.
в. Иногда их наз. также поляризац.
потенциалами, ибо источником, напр.,
Г.
в. Иногда их наз. также поляризац.
потенциалами, ибо источником, напр.,
![]() является
сторонняя электрич. поляризация
является
сторонняя электрич. поляризация
![]() ,
связанная с плотностью внеш. зарядов
,
связанная с плотностью внеш. зарядов
![]() и
токов
и
токов
![]() соотношениями
соотношениями
![]()
Источниками
![]() являются
соответствующие магн. аналоги. Оба
описания взаимно двойственны (см.
Двойственности
перестановочной принцип:
)они переходят друг
являются
соответствующие магн. аналоги. Оба
описания взаимно двойственны (см.
Двойственности
перестановочной принцип:
)они переходят друг
![]() в
друга при заменах
в
друга при заменах![]()
![]()
Смысл
Г. в. состоит в сведении решения системы
Максвелла
уравнений для двух векторных
величин
![]() к
решению неоднородного волнового
уравнения для одного вектора
к
решению неоднородного волнового
уравнения для одного вектора
![]() с
источником
с
источником
![]() или
или
![]() :
:
![]()
Ур-ние (2) и соотношение (1) эквивалентны ур-ниям Максвелла, если поля связаны с Г. в. равенствами
![]()
Использование
Г. в. равносильно описанию поля с помощью
векторного
![]() и
скалярного
и
скалярного
![]() потенциалов
в лоренцевой калибровке (см. Потенциалы
электромагнитного поля;
)при этом
потенциалов
в лоренцевой калибровке (см. Потенциалы
электромагнитного поля;
)при этом
![]()
Однако
градиентная
инвариантность оставляет
ещё нек-рый произвол: к
![]() можно
добавить (без изменения
можно
добавить (без изменения
![]()
![]() )
градиент любой ф-ции y, удовлетворяющей
ур-нию
)
градиент любой ф-ции y, удовлетворяющей
ур-нию
![]() =0.
Благодаря этому поля вне источников
могут быть описаны лишь двумя компонентами
Г. в. Часто в качестве таковых выбирают
к--л. декартову составляющую
=0.
Благодаря этому поля вне источников
могут быть описаны лишь двумя компонентами
Г. в. Часто в качестве таковых выбирают
к--л. декартову составляющую
![]() ,
получая тем самым разделение поля на
поперечно-магн. (TM) и поперечно-электрич.
(ТЕ) моды. Внутри области, содержащей
источники, в общем случае необходимо
привлекать три компоненты Г. в.
,
получая тем самым разделение поля на
поперечно-магн. (TM) и поперечно-электрич.
(ТЕ) моды. Внутри области, содержащей
источники, в общем случае необходимо
привлекать три компоненты Г. в.
Скалярный
потенциал векторного
поля
![]() (чаще
просто потенциал векторного поля) —
это скалярная функция
(чаще
просто потенциал векторного поля) —
это скалярная функция
![]() такая,
что во всех точках области определения
поля
такая,
что во всех точках области определения
поля
![]()
где
![]() обозначает
градиент
.
В физике обычно потенциалом называют
величину, противоположную по знаку
(потенциал силы, потенциал электрического
поля).
обозначает
градиент
.
В физике обычно потенциалом называют
величину, противоположную по знаку
(потенциал силы, потенциал электрического
поля).
Ве́кторный потенциа́л электромагни́тного по́ля (вектор-потенциал, магнитный потенциал) — в электродинамике, векторный потенциал, ротор которого равен магнитной индукции:
![]() .
.
В общем случае для описания произвольного эл.-магн. поля вместо Е и В можно ввести две др. величины: векторный потенциал А (х, у, z, t) и скалярный потенциал фи(x, у, z, t), где х, у, z — координаты, t — время, при этом В и E однозначно выражаются через А и фи:

Ур-ния для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, что упрощает задачу нахождения переменных эл.-магн. полей. Существ. упрощение ур-ний для П. э. п. возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и j выбрать новые потенциалы
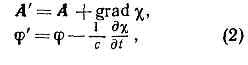
где c — произвольная ф-ция координат и времени, то векторы В и Е, определяемые ур-ниями (1), не изменятся. Инвариантность эл.-магн. поля по отношению к преобразованиям потенциалов (2) носит назв. к а л и б р о в о ч н о й, или г р а д и е н т н о й, и н в а р и а н т н о с т и. Калибровочная инвариантность позволяет наложить на П. э. п. дополнит. условие. Обычно таким дополнит. условием явл. условие Лоренца:
![]()
где e и m — диэлектрич. и магн. проницаемости среды. При использовании условия (3) ур-ния для П. э. п. в однородной среде (e=const, m=const), получаемые из ур-ний Максвелла, приобретают одинаковую форму:
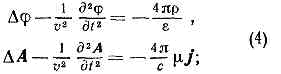
16!!!!!!!!
Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент p (t) которого быстро изменяется во времени.
Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны λ (рис. 2.6.4).
|
Рисунок 2.6.4. Элементарный диполь, совершающий гармонические колебания |
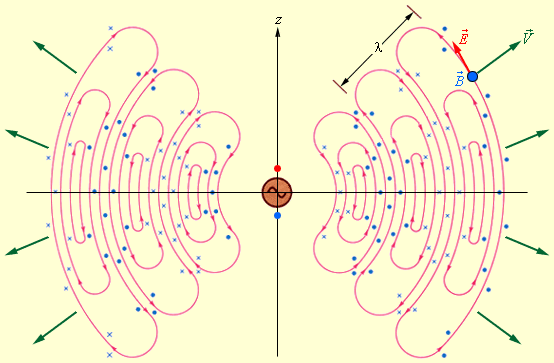
Рис. 2.6.5 дает представление о структуре электромагнитной волны, излучаемой таким диполем.
|
Рисунок 2.6.5. Излучение элементарного диполя |
Следует обратить внимание на то, что максимальный поток электромагнитной энергии излучается в плоскости, перпендикулярной оси диполя. Вдоль своей оси диполь не излучает энергии. Герц использовал элементарный диполь в качестве излучающей и приемной антенн при экспериментальном доказательстве существования электромагнитных волн.
17!!!!!!
Монохроматическое Поле, ЭМ поле, все характеристики которого изменяются во времени по гармоническому закону.
Матем описание:
Монохроматическое поле - это поле, зависящее от времени по гармоническому закону (рис.1.3.1):
|
(1.3.11) |
где
![]() -
амплитуда возмущения (функция
пространственных координат),
-
амплитуда возмущения (функция
пространственных координат),
![]() -
циклическая частота изменения поля во
времени,
-
циклическая частота изменения поля во
времени,
![]() -
фаза поля (функция пространственных
координат).
-
фаза поля (функция пространственных
координат).
 Рис.1.3.1.
Изменение монохроматического поля во
времени.
Рис.1.3.1.
Изменение монохроматического поля во
времени.
Монохроматическое
поле также характеризуется периодом
колебаний
![]() или
частотой
или
частотой
![]() :
:
![]() ,
,
![]() (1.3.12)
причем циклическую частоту
можно
выразить через частоту
:
(1.3.12)
причем циклическую частоту
можно
выразить через частоту
:
![]() ,
,
![]() (1.3.13)
(1.3.13)
Гармоническую
волну характеризуют также пространственный
период - длина
волны
![]() :
:
![]() (1.3.14)
и волновое
число:
(1.3.14)
и волновое
число:
![]() (1.3.15)
(1.3.15)