18.Матричная запись линейных операторов. Собственные значения и собственные векторы линейных операторов.

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Комментарий: порядок базисных элементов предполагается жёстко упорядоченным.

Пусть L- линейное пространство над полем K, A:L→L - линейное преобразование.

Собственным вектором линейного преобразования A называется такой ненулевой вектор x€L, что для некоторого λ€K Ax=λx x€L

Собственным значением линейного преобразования A называется такое число λ€K , для которого существует собственный вектор, то есть уравнение Ax=λx имеет ненулевое решение x€L.

Упрощённо говоря, собственный вектор — любой ненулевой вектор x, который отображается оператором в коллинеарный λx, а соответствующий скаляр λ называется собственным значением оператора.

Собственным подпространством линейного преобразования A для данного собственного числа λ€K (или отвечающим этому числу) называется множество всех собственных векторов x€L , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его E_λ. По определению, E_λ =ker(A- λE) , где E — единичный оператор.

23.Группа.Свойства групп.

Гру́ппа  — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам.

Непустое множество с заданной на нём бинарной операцией называется группой , если выполнены следующие аксиомы:

1. ассоциативность: ;

2. наличие нейтрального элемента: 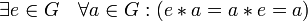(т.е. е является единичным или нейтральным элементом мн-ваG).

3. наличие обратного элемента:

Простейшие свойства

• Обратный к данному элемент всегда определяется однозначно.

• (a⁻¹)⁻¹ = a, a^maⁿ = a^m+n, (a^m)ⁿ = a^mn.

• (ab)⁻¹ = b⁻¹a⁻¹.

• Верны законы сокращения:

,

.

• Обратный элемент к нейтральному есть сам нейтральный элемент.

• Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».

• Пересечение двух подгрупп группы G есть подгруппа группы G.

• Теорема Лагранжа: если G — группа конечного порядка g, то порядок g₁ любой её подгруппы G₁ является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы.

• Для определения числа подгрупп в группе используются теорема Лагранжа и теоремы Силова.

26.Циклические группы.

Группу G называют циклической, если Ea€G :<a>=G

Замечание. Если в качестве бинарной операции рассматривать операцию “+”, то группами являются множества :

C(мн-во комплексных чисел), Z(мн-во целых чисел), Q(множество рациональных, R(мн-во действит.)

Каждая подгруппа циклической группы циклична.

Определение. Непустое подмножество Hмн-ваG называется подгруппой группыG ,если бинарная операция из G замкнутая операция в H.

Обозначение. H<G