
- •1. Понятие вектора и лин. Опер. Над вект-ми. Св-ва опер. Слож. Вект-ов и умнож. Вект-а на число (с док-вом)
- •2. Вычитание
- •2. Линейн. Зависимость векторов (опред-е, св-ва с док-вом)
- •3. Th о коллинеарн. Векторах. Th о компланарн. Веторах
- •4. Th о разлож. Вектора по некомпланарн. Векторам. Коорд. Вектора. Ортонормир. Базис.
- •5. Скалярн. Произв-е векторов. Применение скалярн. Произв-я
- •6. Векторное произв-е (опр-е, вычисл-е, св-ва)
- •7. Смешанное произв-е (опр-е, вычисл-е, св-ва)
- •8. Афинная сист. Коорд. На плоск. И в простр. Декарт. Сист. Корд. Деление отрезка в зад. Отношении
- •9. Ориентация плоскости
- •10. Угол м-у векторами на ориентир. Плоск-ти
- •1 Парал. Перенос
- •2 Поворот осей координат
- •3. Изменение нач. Корд. И поворот осей
- •12. Расст. М-у 2-мя т. Деление отрезка в данном отнош-ии. Прямая линия на плоск. Осн. Виды ур-я прямой на плоск.
- •13. Расст. От т. До прямой. Коорд. Т. Пересеч. Двух прямых. Угол м-у двумя прямыми. Услов. Паралл-ти и перп-ти прямых
- •14. Плоск. В пр-ве. Основн. Виды ур-й плоск. В пр-ве. Услов паралл-ти и перп-ти плоск.
- •15. Неполные ур-я плоск. Расст. От т. До плоск.
- •17. Прям. Линия в простр. Основн. Виды ур-я прямой линии в простр. Угол м-у прямыми. Услов. Паралл-ти и перп-ти 2-х прямых.
- •18. Прямая и плоск. Т. Пересеч. Прямой и плоск. Угол м-у прямой и плоск. Услов. Паралл-ти и перп-ти прямой и плоск.
- •19. Эллипс
- •20. Гипербола
- •21. Парабола
- •22. Поверхн. 2-го пор. Поверхн. Вращ-я. Циллиндрич. Поверхн. Конич. Поверхн. 2-го пор.
- •23. Эллипсоид
- •24. Гиперболоид (однополост., двуполост.)
- •25. Параболоиды (эллиптич., гиперболич.)
- •26. Цилиндры (эллиптич., гиперболич., параболич.)
17. Прям. Линия в простр. Основн. Виды ур-я прямой линии в простр. Угол м-у прямыми. Услов. Паралл-ти и перп-ти 2-х прямых.
M0(x0,y0,z0)
– фиксир. т. прямой L, M L,
||L
, a(l,m,n)
L,
||L
, a(l,m,n)
– направл. вектор прямой (люб. вектор, лежащий на прямой либо || ей)
M(x,y,z)
– произв. т. прямой L. M L
L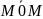 ||
=t*
||
=t*

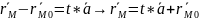 - векторное
ур-е прямой
- векторное
ур-е прямой
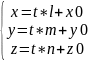 – парам. ур-е
прямой
– парам. ур-е
прямой
Исключ. параметр t:
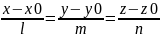 – канонич. ур-е
прямой,
проход. ч-з фиксир. т. M0(x0,y0,z0)
и имеющей направл. вектор
(l,m,n).
– канонич. ур-е
прямой,
проход. ч-з фиксир. т. M0(x0,y0,z0)
и имеющей направл. вектор
(l,m,n).
Пусть
даны 2 т. M1(x1,y1,z1),
M2(x2,y2,z2).
Вектор
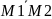 выбер. в кач-ве направл. прямой L, тогда
ур-е прямой примет вид:
выбер. в кач-ве направл. прямой L, тогда
ур-е прямой примет вид:
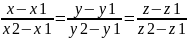 - ур-е
прямой, проходящей ч-з 2 т.
- ур-е
прямой, проходящей ч-з 2 т.
Пусть
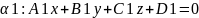 ,
,
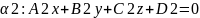 ,
α1||α2
,
α1||α2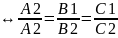 ,
в противн. случ. плоск. пересек. и прямая
пересечения плоск опр-ся ур-ем:
,
в противн. случ. плоск. пересек. и прямая
пересечения плоск опр-ся ур-ем:
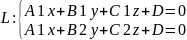 – общее ур-е
прямой
– общее ур-е
прямой
Пусть прямая L зад. линией пересеч. 2-х плоск:
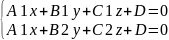
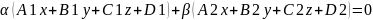 ,
,
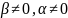 -
это рав-во опр. плоск., кот. прох. ч-з
прямую L.
-
это рав-во опр. плоск., кот. прох. ч-з
прямую L.
Совокупность всех плоскостей, прох. ч-з одну и ту же прямую, назыв. пучком плоскостей.
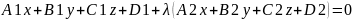 ,
,
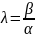 – опред. все плоскости пучка, кроме 2-й
из задающих прямую.
– опред. все плоскости пучка, кроме 2-й
из задающих прямую.
Пусть
зад. направл. векторы 2-х прямых
 ||
||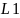 ,
,
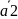 ||
||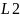 ,
(l1,m1,n1),
(l2,m2,n2)
,
(l1,m1,n1),
(l2,m2,n2)
Угол
м-у прямыми
приним. равным углу м-у направл-ми
векторами:

L1||L2
||
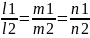
L1 L2
L2
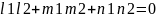
18. Прямая и плоск. Т. Пересеч. Прямой и плоск. Угол м-у прямой и плоск. Услов. Паралл-ти и перп-ти прямой и плоск.
Коорд. т. пересеч. прямой L и плоск. α должны одноврем. удовл. ур-ям:

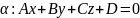
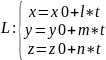
Подставляя их в ур-е плоск, получ. знач. парам. t
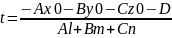
Подставляя найд. t в парам. ур-я прямой, получ. корд. т. пересеч. прямой и плоск.
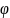 - угол м-у прямой
и плоск,
- угол м-у прямой
и плоск,
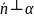 ,
||L
,
||L
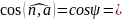
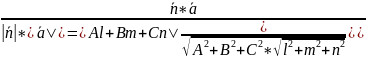


 – угол м-у прямой
и плоск.
– угол м-у прямой
и плоск.
L
α
||
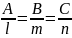
L||α
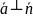
*
=0
Al+Bm+Cn=0
*
=0
Al+Bm+Cn=0
19. Эллипс
Эллипсом назыв. геом. место точек M(x;y), для кот. сумма расстояний до 2-х зад. т. F1(c;0) ,F2(-с;0), назыв. фокусами эллипса, постоянна и равна 2а.
По
опр-ю |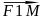 |+|
|+|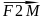 |=2a,
|=2a,
|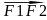 |=2c,
a>c
|=2c,
a>c
Восп-ся форм-ми расст. м-у 2-мя т:
|
|=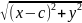 =
=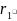 ; |
|=
; |
|= =
=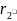
r1+r2=2a
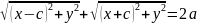
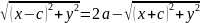
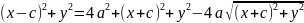
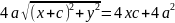
 :возводим в квадрат
и группируем
:возводим в квадрат
и группируем
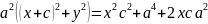
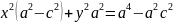
т.к
a>c,
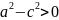
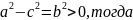
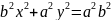
x2/a2 + y2/b2 =1 - канонич. ур-е эллипса
Эл-ты эллипса:
О – центр эллипса, ABCD – вершины эллипса
F1(c;0), F2(-с;0) - фокусы эллипса
2с
- фокусное расстояние, кот. вычисл. по
ф-ле с=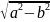
AC=2a, BD=2b - большая и малая полуоси эллипса
Ɛ=с/a
(Ɛ
<1) - эксцентриситет
эллипса, Ɛ
=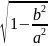 .
.
Эксцентриситет опр-ся отношением осей эллипса и характериз.т его форму.
Прямые, парал. малой оси и отстоящие от нее на расстояние a/Ɛ, назыв. директрисами эллипса. Ур-е директрисы:
X=±a/ Ɛ ; a/ Ɛ >a т.е Ɛ <1
Фокальный
параметр P=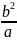 - это половина хорды, провед. ч-з фокус,
параллельно малой оси.
- это половина хорды, провед. ч-з фокус,
параллельно малой оси.
Окружность предст. собой геом. место точек, равноудал. от т. О, назыв. центром окружн-ти, a=b=п
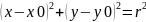 – ур-е окружн. с
центром (x0,y0)
и радиусом r.
– ур-е окружн. с
центром (x0,y0)
и радиусом r.
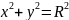 – канонич.
ур-е окружн.
– канонич.
ур-е окружн.
20. Гипербола
Гиперболой назыв. геом. место точек M(x;y), для кот. абсол. величина разности расстояний до 2-х зад. т. F1(c;0) ,F2(-с;0), назыв. фокусами гиперболы, постоянна и равна 2а (a<c)
По
опр-ю | |=2a,
|
|=2c
|=2a,
|
|=2c
Найдем:|
|=
=
,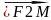 |=
=
|=
=
|r1-r2|=2a; r1-r2=±2a
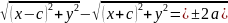
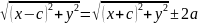
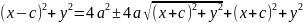

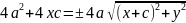
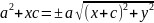
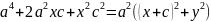
 *(-1)
*(-1)
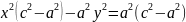
 ,
т.к. по услов. C>a
,
т.к. по услов. C>a

X2/a2 - y2/b2 =1 - канонич. ур-е гиперболы
Эл-ты гиперболы:
О – центр гиперболы, A,B – вершины гиперболы
F1(c;0) ,F2(-с;0) – фокусы гиперболы
2с
- фокусное расстояние, кот. вычисл. по
ф-ле
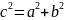
AB=2a – действит.. ось гиперболы.
СD=2b – мнимая ось гиперболы
Ɛ=с/a - эксцентриситет гиперболы,
Ɛ
=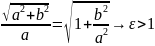
Эксцентритет опр-ся отношением осей гиперболы и характеризует ее форму: чем больше эксцентриситет, тем более вытянут вдоль мнимой оси основной прямоуг-к гиперболы.
Ур-я директрис имеют вид: х=±a/Ɛ ; т.к Ɛ >1 то a/Ɛ <a
Асимптоты гиперболы – это прямые, к кот. ветви гиперболы неограниченно приближаются при удалении на бесконечность
k=±tgα=±b/a
y=kx=±
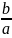 *x
– ур-я асимптоты
*x
– ур-я асимптоты
Фокальный параметр P=
