20. Представление логических функций в алгебре Жегалкина.

В ряде случаев, преобразования над формулами булевых функ-ций удобно призводить в алгебре Жегалкина. Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение по модулю 2 (*, (прим. далее + ) ), а также константу 1. Здесь имеют место те же законы:

• х + y = y + х, х у = у х (закон коммутативности);

• х + (у + z) = (х + у) + z, х(у z) = (х у)z (закон ассоциативности);

• x (y + z) = x y + x z (закон дистрибутивности).

Для упрощения формул могут быть использованы следующие соотношения: х + 0 = х; х 1 = х; х 0 = 0; х + х = 0; х х = х. Из коммутативности и ассоциативности дизъюнкции следует, что дизъюнкция нескольких переменных может выполняться последовательно, причем порядок взятия дизъюнкции не влияет на результат."

21.Логические элементы

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.

С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана о экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.

Логические элементы выполняют логическую функцию (операцию) с входными сигналами (операндами, данными).

Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.

Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).

Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).

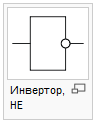
Инвертор, НЕ

0 1

1 0

Мнемоническое правило для отрицания звучит так: На выходе будет:

«1» тогда и только тогда, когда на входе «0»,

«0» тогда и только тогда, когда на входе «1»

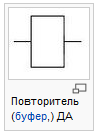
Повторение, ДА

Повторитель (буфер,) ДА

0 0

1 1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)

2И ٨

0 0 0

1 0 0

0 1 0

1 1 1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

«1» тогда и только тогда, когда на всех входах действуют «1»,

«0» тогда и только тогда, когда хотя бы на одном входе действует «0»

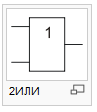
Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)

2ИЛИ

0 0 0

1 0 1

0 1 1

1 1 1

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:

«1» тогда и только тогда, когда хотя бы на одном входе действует «1»,

«0» тогда и только тогда, когда на всех входах действуют «0»

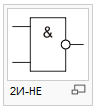
Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)

2И-НЕ

0 0 1

0 1 1

1 0 1

1 1 0

Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

«1» тогда и только тогда, когда хотя бы на одном входе действует «0»,

«0» тогда и только тогда, когда на всех входах действуют «1»

Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)

2ИЛИ-НЕ ↓

0 0 1

0 1 0

1 0 0

1 1 0

Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

«1» тогда и только тогда, когда на всех входах действуют «0»,

«0» тогда и только тогда, когда хотя бы на одном входе действует «1»

[править]

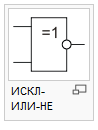
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ

ИСКЛ-ИЛИ-НЕ ↔

0 0 1

0 1 0

1 0 0

1 1 1

Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:

«1» тогда и только тогда, когда на входе действует четное количество,

«0» тогда и только тогда, когда на входе действует нечетное количество

[править]

Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

В англоязычной литературе 2XOR.

0 0 0

0 1 1

1 0 1

1 1 0

Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:

«1» тогда и только тогда, когда на входе действует нечётное количество ,

«0» тогда и только тогда, когда на входе действует чётное количество

[править]

Импликация от A к B (инверсия декремента) →

0 0 1

0 1 1

1 0 0

1 1 1

Мнемоническое правило для инверсии декремента звучит так: На выходе будет:

«0» тогда и только тогда, когда на «B» меньше «А»,

«1» тогда и только тогда, когда на «B» больше либо равно «А»

Импликация от B к A (инверсия инкремента) →

0 0 1

0 1 0

1 0 1

1 1 1