- •1. Задача, о площади криволинейной трапеции приводящая к понятию определенного интеграла.
- •2. Классы интегрируемых функций.
- •3. Теорема об определенном интеграле с переменным верхним пределом
- •4. Теорема Лейбница – Ньютона.
- •5. Теорема об интегрировании по частям
- •6. Теорема о замене переменной в определенном интеграле
- •7. Вывод формулы вычисления площади плоской фигуры (в декартовой системе координат)
- •8. Вывод формулы вычисления длины дуги (в декартовой системе координат)
- •9. Вывод формулы вычисления объема тела вращения относительно оси ox и oy (в декартовой системе координат).
- •10. Теорема об абсолютной сходимости несобственного интеграла 1-го рода
- •11. Сформулируйте и докажите свойства решений олду.
- •12. Теорема о равенстве нулю вронскиана линейно-зависимых функций (необх. Усл. Л.З.).
- •14. Теорема о структуре общего решения лнду
- •15. Теорема о суперпозиции решений (принцип сложения решений)
- •16. Метод вариации произвольных постоянных – метод Лагранжа
- •17. Необходимый признак сходимости.
- •18. Критерий сходимости рядов с неотрицательными членами.
- •19. Предельный признак сравнения для рядов с неотрицательными членами.
- •20. Признак Даламбера.
- •21. Радикальный признак Коши.
- •22. Абсолютная и условная сходимость. Достаточный признак сходимости знакопеременных рядов.
- •23. Степенные ряды. Теорема Абеля. Радиус сходимости.
- •24.Тригонометрический ряд Фурье. Нахождение коэффициентов для четных и нечетных функций.
- •25. Нахождение коэффициентов для тригонометрического р. Фурье (теорему док).
8. Вывод формулы вычисления длины дуги (в декартовой системе координат)
Пусть
дуга – это график некоторой функцией
f(x),
заключенный между x
= a,
x
= b.
Пусть f(x)
– определена на [a;
b].
Разобьем [a;
b]
на n
частей произвольным образом. Обозначим
Δxk
= xk
– xk
– 1.
Через точки xi
проведем вертикальные линии, параллельные
Oy.
Обозначим точки пересечения графика с
этими линиями M1,
M2,
… , Mn-1
и соединим их. Длина ломанной
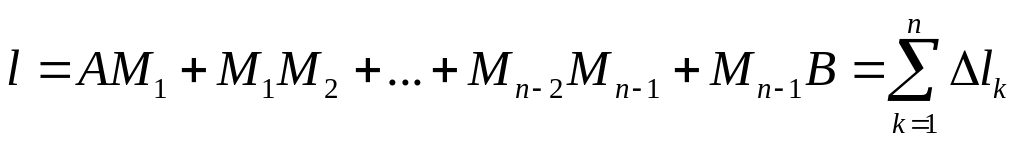 ,
где
,
где
![]() .
.
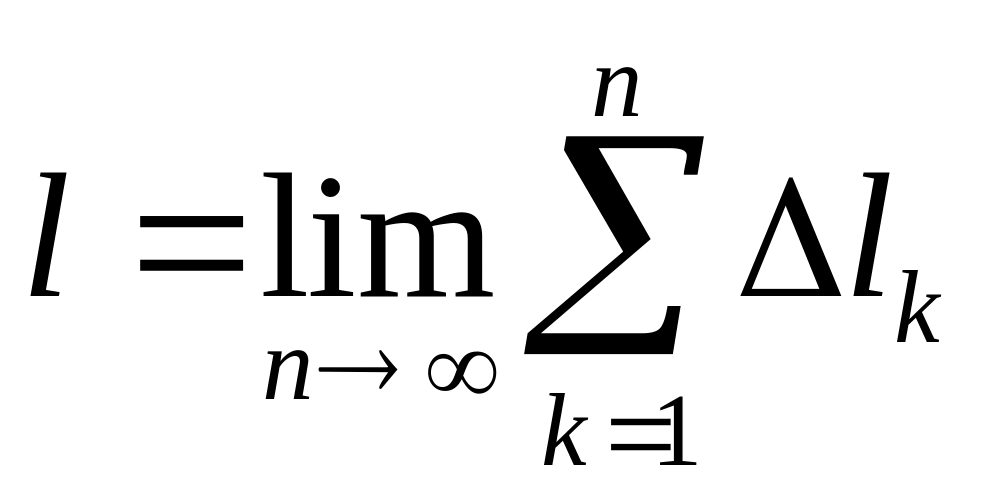
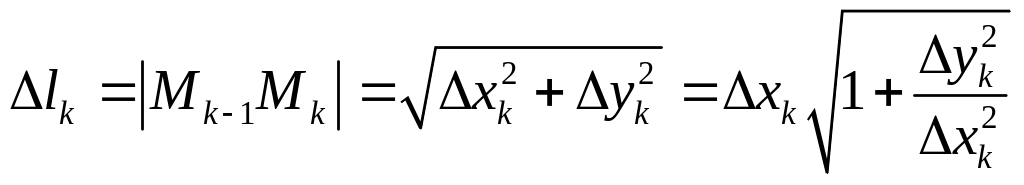
По теореме Лагранжа:
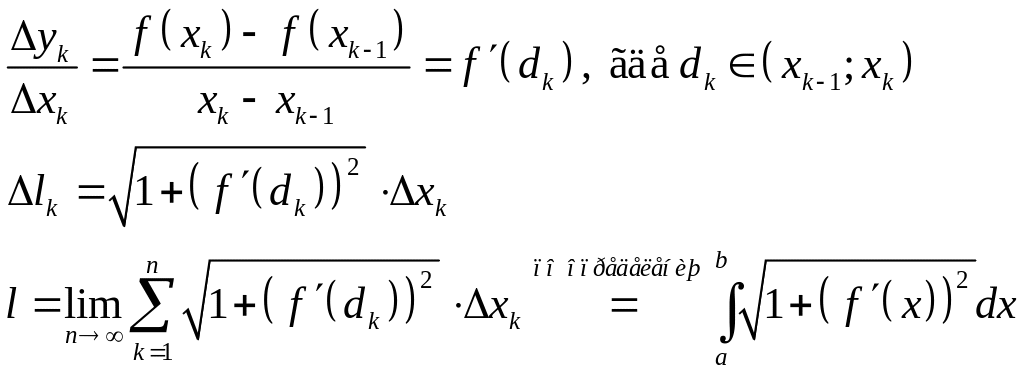
Если дуга задана параметрически, то:
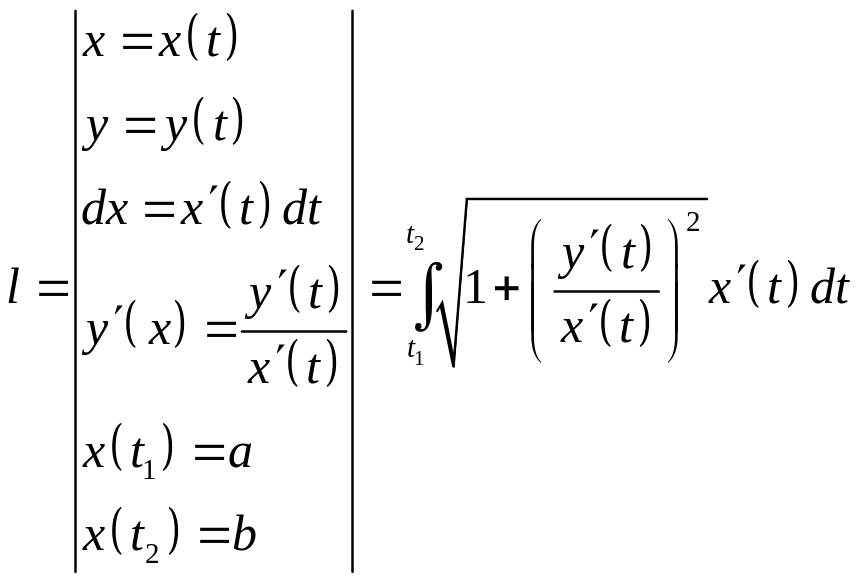
9. Вывод формулы вычисления объема тела вращения относительно оси ox и oy (в декартовой системе координат).
Пусть задано тело, ограниченное замкнутой поверхностью, известно S любого сечения плоскостью, перпендик. к OX –(поперечное)
1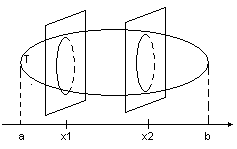 .
Разбив отрезок [a,b]
на n
частей a=Xₒ<X₁<X₂...<Xn=b
.
Разбив отрезок [a,b]
на n
частей a=Xₒ<X₁<X₂...<Xn=b
Обозначим ΔXk=Xk-Xk-1 , k=1,n
λ=max[a,b]{ΔXk}, через xk проводим поперечное сечение
2.
Выберем ξk![]() [xk-1,
xk]
произвольно и найдем S(ξk);
каждый слой тела Т представляет собой
цилиндр с основанием S(ξk)
и высотой ΔXk
[xk-1,
xk]
произвольно и найдем S(ξk);
каждый слой тела Т представляет собой
цилиндр с основанием S(ξk)
и высотой ΔXk
ΔVk= S(ξk) ΔXk
V=![]()
V =
=![]()
Вычисление объема тела вращения: Рассмотрим тело, образованное вращением вокруг оси Ox криволинейной трапеции aABb ограниченной кривой y=f(x), осью Ox и x = a, y = b
1. Рассмотрим произвольное разбиение [a,b] x0 = a < x1< x2<… < xn = b
обозначим
Δxk
= xk-xk-1
![]()
![]()
2. Пересекаем тело вращения плоскостями перпендикулярными Ox и получи круги, радиусы которых равны |yk|=|f(xk)| На каждом [xk-1- xk] выберем произвольным образом ξk S(ξk)= πf2(ξk) (S=πR2)
3.
Предположим на любом частном отрезке
ф-ия S=S(x)
совпадает с S(ξk).
Тогда объем частичного цилиндра: ΔVk
= S(ξk)Δxk
= πf2(ξk)Δxk
![]()
4.
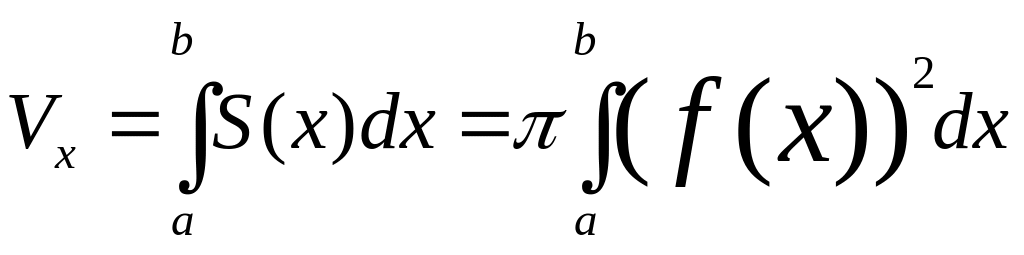
![]()
10. Теорема об абсолютной сходимости несобственного интеграла 1-го рода
Несобственный
интеграл первого или второго рода
![]() называется абсолютно сходящимся, если
сходиться интеграл, составленный из
модулей
называется абсолютно сходящимся, если
сходиться интеграл, составленный из
модулей
![]() ;
несобственный интеграл называется
условно сходящимся, если он сходиться,
но не абсолютно (
-расходиться).
;
несобственный интеграл называется
условно сходящимся, если он сходиться,
но не абсолютно (
-расходиться).
Теорема:
Если несобственный интеграл абсолютно сходиться, то он просто сходиться.
Доказательство:
Пусть - сходиться, рассмотрим 2 вспомогательные операции:
![]() (*)
(*)
![]()
![]()
![]() ;
;
![]()
сх-ся
![]() сх-ся сх-ся
сх-ся
сх-ся сх-ся
сх-ся
Из
(*) следует, что
![]() сходиться.
сходиться.
11. Сформулируйте и докажите свойства решений олду.
1) Если у1(х) – решение ОЛДУ у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0 (*) , то функция y=С у1(х), где С=const, также является решением этого ОЛДУ.
Док-во:
Подставим
![]() в ДУ:
в ДУ:
С у1(n) + P1 С y1(n-1) +…+ Pn-1 С y1’ + Pn С y1 = 0
С(у1 (n) + P1 у1(n-1) +…+ Pn-1 у1’ + Pn у1) = 0
у1(n) + P1 у1(n-1) +…+ Pn-1 у1’ + Pn у1 = 0
![]()
2) Если у1(х) и у2(х) – решение ОЛДУ (*), то функции у1(х) + у2(х) также являются решениями этого ДУ
Док-во:
(у1+у2)(n) + P1(у1+у2) (n-1) +…+ Pn-1 (у1+у2)’ + Pn (у1+у2) =
= [у1 (n) + P1 у1 (n-1) +…+ Pn-1 у1’ + Pn у1] + [у2 (n) + P1 у2 (n-1) +…+ Pn-1 у2’ + Pn у2] = 0 + 0 = 0
3) Если y1, y2, …, yk – решения ЛОДУ (*), то функция (C1y1 + C2y2 + … + Ckyk) тоже является решением этого ДУ для любых постоянных C1, C2, …, Ck.