Вопрос 11.3. Признаки сходимости знакопостоянных рядов.

Теорема 11.1. Если все частичные суммы ряда с неотрицательными членами ограничены одним и тем же числом, то ряд сходится.

Доказательство. Пусть существует число , такое, что для всех n. Так как частичные суммы образуют монотонно неубывающую последовательность ограниченную сверху, то такая последовательность всегда сходится и имеет предел. Обозначим его через S. Тогда S есть сумма исходного ряда, то есть ряд сходится.

Конец доказательства.

Теорема 11.2. (1-й признак сравнения). Пусть даны два ряда и с неотрицательными членами. Тогда если для всех n , то из сходимости ряда следует сходимость ряда , а из расходимости ряда вытекает расходимость ряда .

Доказательство. Пусть ряд сходится и его сумма равна . Тогда в силу имеем для любого n. Поэтому по теореме 11.1 ряд сходится. Пусть теперь расходится ряд . Тогда в силу частичные суммы образуют монотонно неубывающую неограниченную сверху последовательность. В силу для любого n последовательность частичных сумм ряда так же неограниченна сверху. Поэтому этот ряд расходится.

Конец доказательства.

Теорема 11.3 (2-й признак сравнения). Пусть даны два знакопостоянных ряда и . Тогда если существует конечный придел 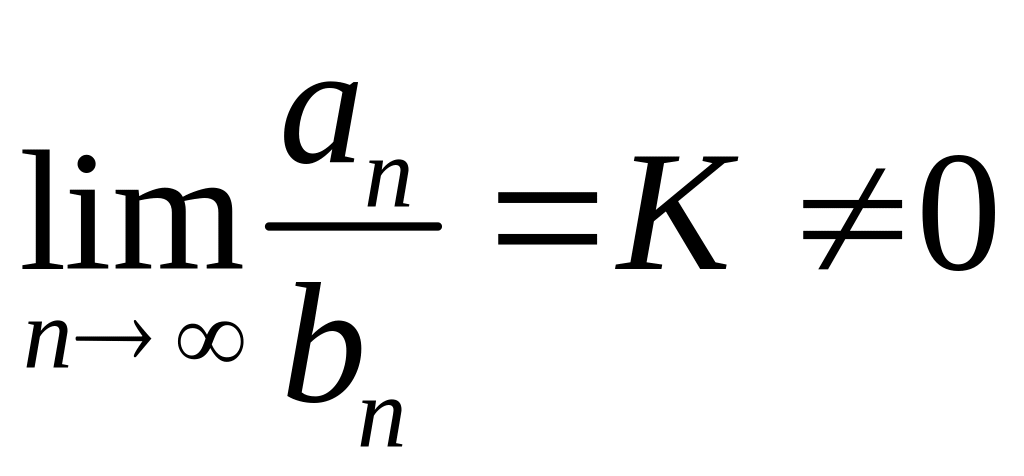, то оба ряда сходятся или расходятся одновременно.

Доказательство. Пусть задано , тогда существует натуральное число N(e), такое, что 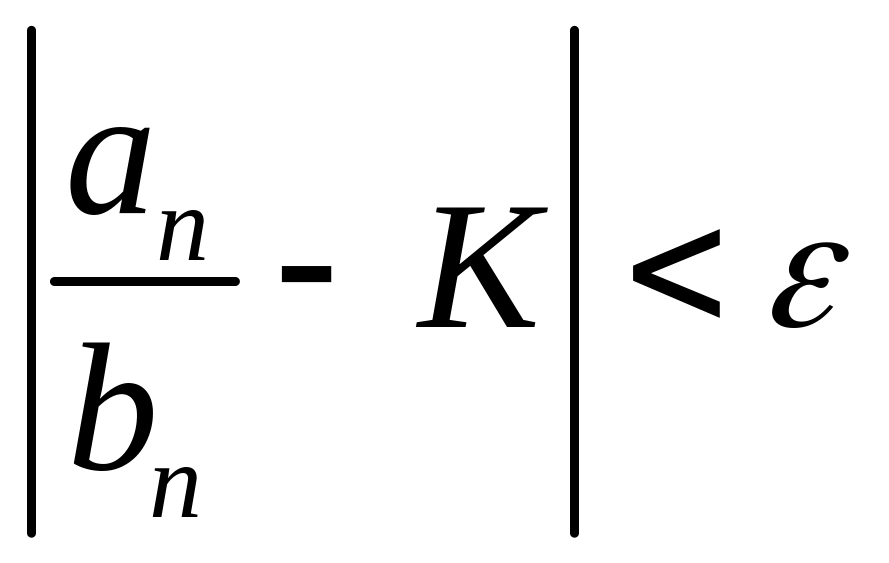для всех . Отсюда следует, что для всех . Так как ряд сходится, то сходятся и ряды, полученные умножением этих чисел на множители и . Тогда по теореме 11.2 следует, что ряды сходятся или расходятся одновременно.

Конец доказательства.

Пример 11.5. Пусть дан ряд . Выберем для сравнения ряд . Этот ряд расходится, вычислим предел , следовательно, исходный ряд расходится.

Конец пример.

Пример 11.6. Пусть дан ряд . Выберем для сравнения ряд . Выше было показано, что этот ряд сходится. Так как , то по второму признаку сравнения исходный ряд сходится.

Конец примера.

Теорема 11.4 (признак Даламбера). Пусть дан ряд co знакоположительными членами и пусть 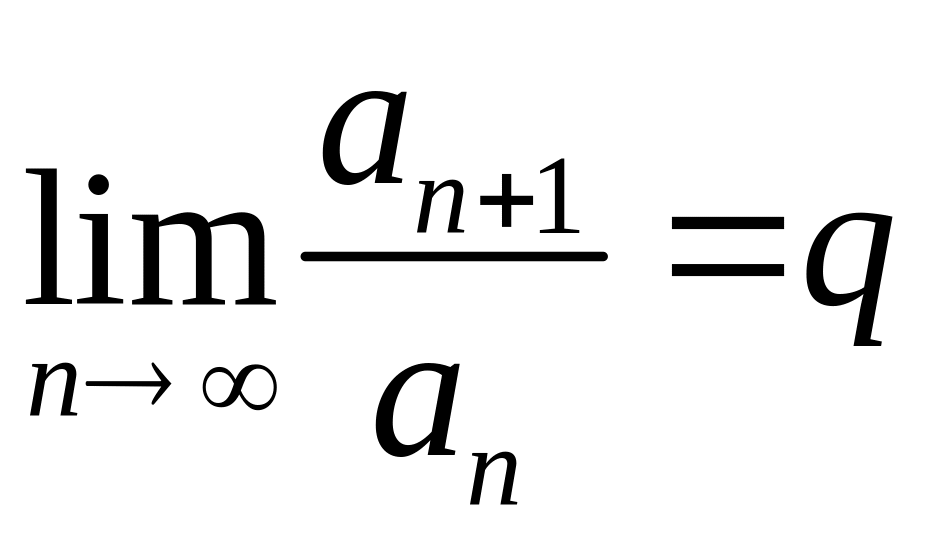. Тогда, если , то ряд сходится, если , то ряд расходится. Если , то ни чего определенного сказать нельзя, то есть ряд может сходится, а может и расходится. Эта теорема приводится без доказательства.

Пример 11.7. Исследовать на сходимость ряд . Применим признак Даламбера. Для этого вычислим предел отношения 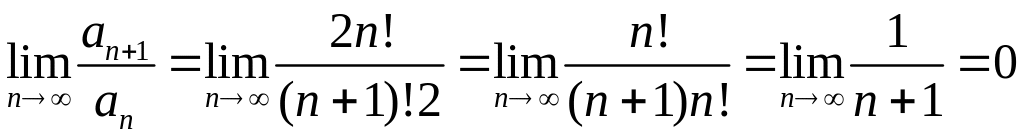, следовательно, по признаку Даламбера ряд сходится.

Конец примера.

Теорема 11.5. Пусть дан ряд со знакоположительными членами и пусть . Тогда при ряд сходится, а при ряд расходится, при возникает неопределенная ситуация, то есть ряд может сходиться, а может и расходиться. Эта теорема приводится без доказательства.

Замечание 11.6. Величина q в признаках Даламбера и Коши одна и та же, а именно справедливо равенство .

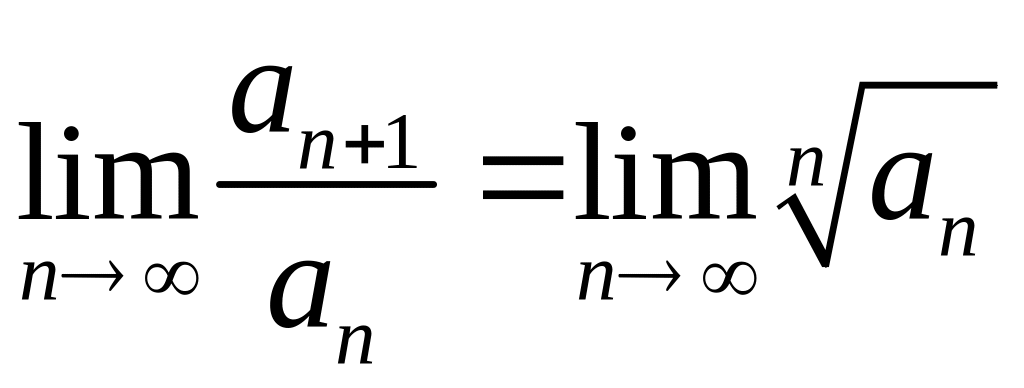Конец замечания.

Пример 11.8. Исследовать на сходимость ряд .

Применим признак Коши. Вычислим предел 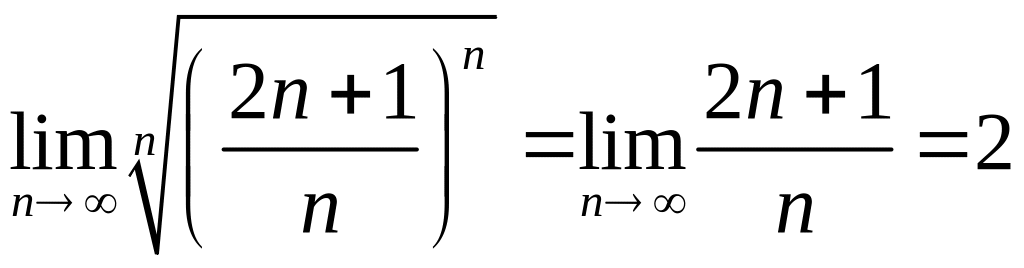, отсюда следует, что ряд расходится.

Конец примера.