8. Доверительный интервал для оценки математического ожидания нормального распределения при нормальном распределении при известном СКО. Доверительный интервал для оценки математического ожидания нормального распределения при нормальном распределении при неизвестном СКО. Распределение Стьюдента. Оценка истинного значения измеряемой величины.

Доверительный интервал для оценки математического ожидания нормального распределения при нормальном распределении при известном СКО

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение Ϭ этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней . Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью γ.

Будем рассматривать выборочную среднюю как случайную величину ( изменяется от выборки к выборке) и выборочные значения признака — как одинаково распределенные независимые случайные величины (эти числа также изменяются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно а и среднее квадратическое отклонение - σ.

Примем без доказательства, что если случайная величина X распределена нормально, то выборочная средняя , найденная по независимым наблюдениям, также распределена нормально. Параметры распределения таковы:

М( ) = а, σ( ) = σ/ .

Потребуем, чтобы выполнялось соотношение

где γ — заданная надежность.

Пользуясь формулой

) = 2Ф( / σ),

заменив X на и σ на σ (Х) = . получим

Р (| а | < ) = 2Ф ( / σ) = 2Ф (t),

где t = / σ.

Найдя из последнего равенства = tσ/ , можем написать

Р (| а | < tσ/ ) = 2Ф (t);

Приняв во внимание, что вероятность Р задана и равна γ. окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через )

P( tσ/ tσ/ ) = 2Ф(t) = γ.

Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал ( tσ/ tσ/ ) покрывает неизвестный параметр а; точность оценки = tσ/ .

Итак, поставленная выше задача полностью решена. Укажем еще, что число t определяется из равенства 2Ф(t) = γ, или Ф(t) = γ/2; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное γ/2.

Доверительный интервал для оценки математического ожидания нормального распределения при нормальном распределении при неизвестном СКО

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение о неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором о предполагалось известным.

Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t):

,

которая имеет распределение Стьюдента с k = n—1 степенями свободы; здесь

—выборочная средняя, S—«исправленное» среднее квадратическое отклонение, n—объем выборки.

Плотность распределения Стьюдента

где .

Мы видим, что распределение Стьюдента определяется параметром n—объемом выборки (или, что то же, числом степеней свободы k = n—1) и не зависит от неизвестных параметров a и σ; эта особенность является его большим достоинством. Поскольку S(t, n) — четная функция от t, вероятность осуществления неравенства

определяется так:

Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим

Итак, пользуясь распределением Стьюдента, мы нашли

доверительный интервал , покрывающий неизвестный параметр а с надежностью .

Здесь случайные величины X и S заменены неслучайными величинами х и s, найденными по выборке. По заданным n и можно найти .

Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если n=5 и γ=0,99, то, пользуясь распределением Стьюдента, найдем = 4,6, а используя функцию Лапласа, найдем = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.

Пояснение. Ранее было указано, что если Z—нормальная величина, причем M(Z) = 0, σ(Z) = 1, а V—независимая от Z величина, распределенная по закону с k степенями свободы, то величина

(*)

распределена по закону Стьюдента с k степенями свободы.

Пусть количественный признак X генеральной совокупности распределен нормально, причем М(Х) = а, σ(Х) =σ. Если из этой совокупности извлекать выборки объема n и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем

М(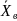 ) = а, σ( ) = σ/ .

Тогда случайная величина

(**)

также имеет нормальное распределение как линейная функция нормального аргумента , причем M(Z)= 0, σ(Z)=l.

Доказано, что случайные величины Z и

(***)

независимы ( —исправленная выборочная дисперсия) и что величина V распределена по закону с k = n—1 степенями свободы.

Следовательно, подставив (**) и (***) в (*), получим величину

Т = (( ) )/S,

которая распределена по закону Стьюдента с k = n—1 степенями свободы.

Распределение Стьюдента

Пусть Z—нормальная случайная величина, причем M(Z) = 0, σ(Z) = 1, а V—независимая от Z величина, которая распределена по закону с k степенями свободы. Тогда величина

(*)

имеет распределение, которое называют t-распределением или распределением Стьюдента (псевдоним английского статистика В. Госсета), с k степенями свободы.

Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы.

С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

Оценка истинного значения измеряемой величины

Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины . Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии 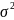(измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в двух предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.

8. Доверительный интервал для оценки ско σ нормального распределения. Распределение хи-квадрат.

Доверительный интервал для оценки СКО σ нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение σ по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр σ с заданной надежностью γ.

Потребуем, чтобы выполнялось соотношение

Р( |σ—s|<δ) = γ, или Р (s—δ < σ < s+δ) = γ.

Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство

s—δ< σ < s+ δ

в равносильное неравенство

s (1 — δ /s) < σ < s (1 + δ /s).

Положив δ/s = q, получим

s(l— q)<a <s(l+q). (*)

Остается найти q. С этой целью введем в рассмотрение случайную величину «хи»:

,

где n—объем выборки.

Величина распределена по закону с n—1 степенями свободы, поэтому квадратный корень из нее обозначают через

Плотность распределения имеет вид

(**)

Это распределение не зависит от оцениваемого параметра σ, а зависит лишь от объема выборки n.

Преобразуем неравенство (*) так, чтобы оно приняло вид < < . Вероятность этого неравенства равна заданной вероятности γ, т. е.

Предполагая, что q < 1, перепишем неравенство (*) так:

Умножив все члены неравенства на S , получим

или

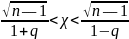
Вероятность того, что это неравенство, а следовательно, и равносильное ему неравенство (*) будет осуществлено, равна

Из этого уравнения можно по заданным n и γ найти q.

Вычислив по выборке s и найдя по таблице q, получим искомый доверительный интервал (*), покрывающий а с заданной надежностью γ, т. е. интервал

Распределение хи-квадрат

Пусть Xi(I = 1, 2, ..n)— нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение — единице. Тогда сумма квадратов этих величин

распределена по закону («хи квадрат») с k = n степенями свободы; если же эти величины связаны одним линейным соотношением, например , то число степеней свободы k = n — 1.

Плотность этого распределения

где — гамма-функция; в частности,

Г(n+1)=n!.

Отсюда видно, что распределение «хи квадрат» определяется одним параметром—числом степеней свободы k.

С увеличением числа степеней свободы распределение медленно приближается к нормальному.

8. Точечная и интервальная оценка вероятности биномиального распределения с заданной надежностью γ по относительной частоте.

Пусть производятся независимые испытания с неизвестной вероятностью р появления события А в каждом испытании. Требуется оценить неизвестную вероятность р по относительной частоте, т. е. надо найти ее точечную и интервальную оценки.

А. Точечная оценка. В качестве точечной оценки неизвестной вероятности р принимают относительную частоту

W = m/n,

где m—число появлений события А; n—число испытаний.

Эта оценка несмещенная, т. е. ее математическое ожидание равно оцениваемой вероятности. Действительно, учитывая, что М(m) = nр, получим

М (W) = М [m/n] = М (m)/n — nр/n — р.

Найдем дисперсию оценки, приняв во внимание, что D(m) = npq:

D (W) = D [m/n] — D (m)/n² = npq/n² = pq/n.

Отсюда среднее квадратическое отклонение.

σ_w — = .

Б. Интервальная оценка. Найдем доверительный интервал для оценки вероятности по относительной частоте. Напомним, что ранее была выведена формула, позволяющая найти вероятность того, что абсолютная величина отклонения не превысит положительного числа δ:

Р (| X - а | < δ) = 2Ф (δ /а), (*)

где X — нормальная случайная величина с математическим ожиданием М(Х) = а.

Если n достаточно велико и вероятность р не очень близка к нулю и к единице, то можно считать, что относительная частота распределена приближенно нормально, причем, как показано в п. A, M(W) = p.

Таким образом, заменив в соотношении (*) случайную величину X и ее математическое ожидание а соответственно случайной величиной W и ее математическим ожиданием р, получим приближенное (так как относительная частота распределена приближенно нормально) равенство

Р (| W—р | <δ) = 2Ф (δ/<σ_w). (**)

Приступим к построению доверительного интервала (p₁,p₂), который с надежностью γ покрывает оцениваемый параметр р. Потребуем, чтобы с надежностью γ выполнялось соотношение (**):

P(|W— р|< δ) = 2Ф(δ /σ) = γ.

Заменив σ_w через √(pq/n) (см. п. А), получим

P(|W—р|<δ) = 2Ф(δ √(n)/√(pq)) = 2Ф (t) = γ,

где t = δ√(n)√(pq).

Отсюда

δ=t√(pq/n),

следовательно,

P(|W—р| < √(pq/n)) = 2Ф (t) = γ.

Таким образом, с надежностью γ выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1—р вместо q):

| w—p | < t √(p(p-1)/n).

Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда

w—p < t√(p(1—p)/n).

Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно р:

[(t²/n)+ 1)] р²—2 [w + (t²/n)] Рp+ w² < 0.

Дискриминант трехчлена положительный, поэтому его корни действительные и различные: меньший корень

больший корень

Итак, искомый доверительный интервал p₁ < р < p₂, где р₁ и р₂ находят по формулам (***) и (****).

При выводе мы предположили, что w > р; тот же результат получим при w < р.