3.2 Схема алгоритма

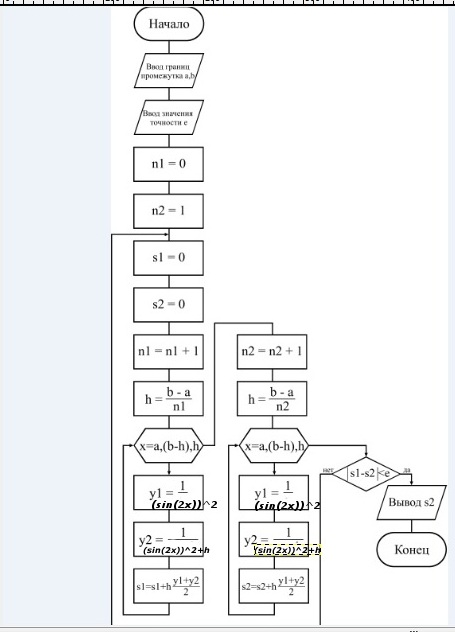
Рис. 2.2

3.3 Текст программы

CLS

Const pi = 3.14

A = pi/3

B = pi/2

PRINT "e=";

INPUT e

n1 = 0

n2 = 1

DO

s1 = 0

s2 = 0

n1 = n1 + 1

h = (b - a) / n1

FOR x = a TO (b - h) STEP h

y1 = 1 / (sin(2*x)^2)

y2 = 1 / ((sin(2*x))^2+h)

s1 = s1 + ((y2 + y1) * h) / 2

NEXT x

n2 = n2 + 1

h = (b - a) / n2

FOR x = a TO (b - h) STEP h

y1 = 1 / (sin(2*x))^2

y2 = 1 / ((sin(2*x))^2 + h)

s2 = s2 + ((y2 + y1) * h) / 2

NEXT x

LOOP UNTIL ABS(s2 - s1) < e

PRINT "s="; s2

Проверка предоставлена в пункте 5

3.4 Результат работы программы

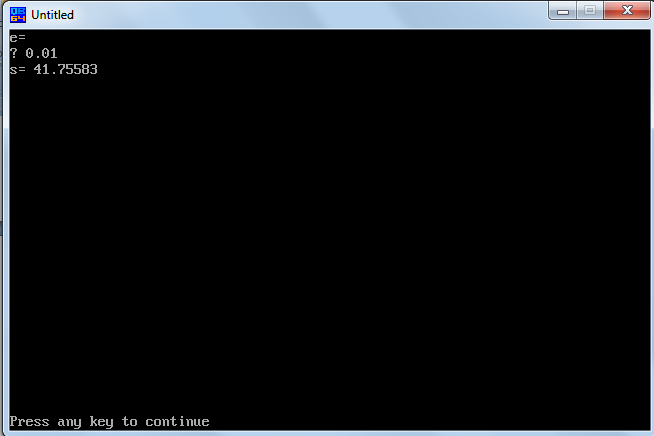
Рис. 2.3

3.Решение нелинейного уравнения

Общие сведения.

Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить

уравнение это значит найти такое x, при котором уравнение превращается в

тождество. В общем случае уравнение может иметь 0; 1; 2;...∞ корней.

Рассмотренные ниже численные методы решения нелинейных уравнений

позволяют находить один корень на заданном интервале [a,b]. При этом на

интервале должен существовать только один корень.

Решение уравнения складывается из двух этапов:

1. отделения корня, т.е. грубой оценки значения корня, которое используется в

качестве начального приближения при его последующем уточнении;

2. уточнения корня, т.е. доведения его численного значения до заданной степени

точности.

Для отделения корня (определения начального приближения) следует

пользоваться графическим методом. Уточнение корня может быть произведено

одним из следующих методов.

3.1 Решение нелинейного уравнения методом хорд-касательных.

Описание метода:

Если в методе касательных производную функцию F’(Xi) заменить отношением конечных приращений, то получаем расчетную формулу для метода

X(i+1)=x(i)-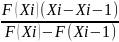

Исходные данные: x=tan(x)

3.2 График заданной функции

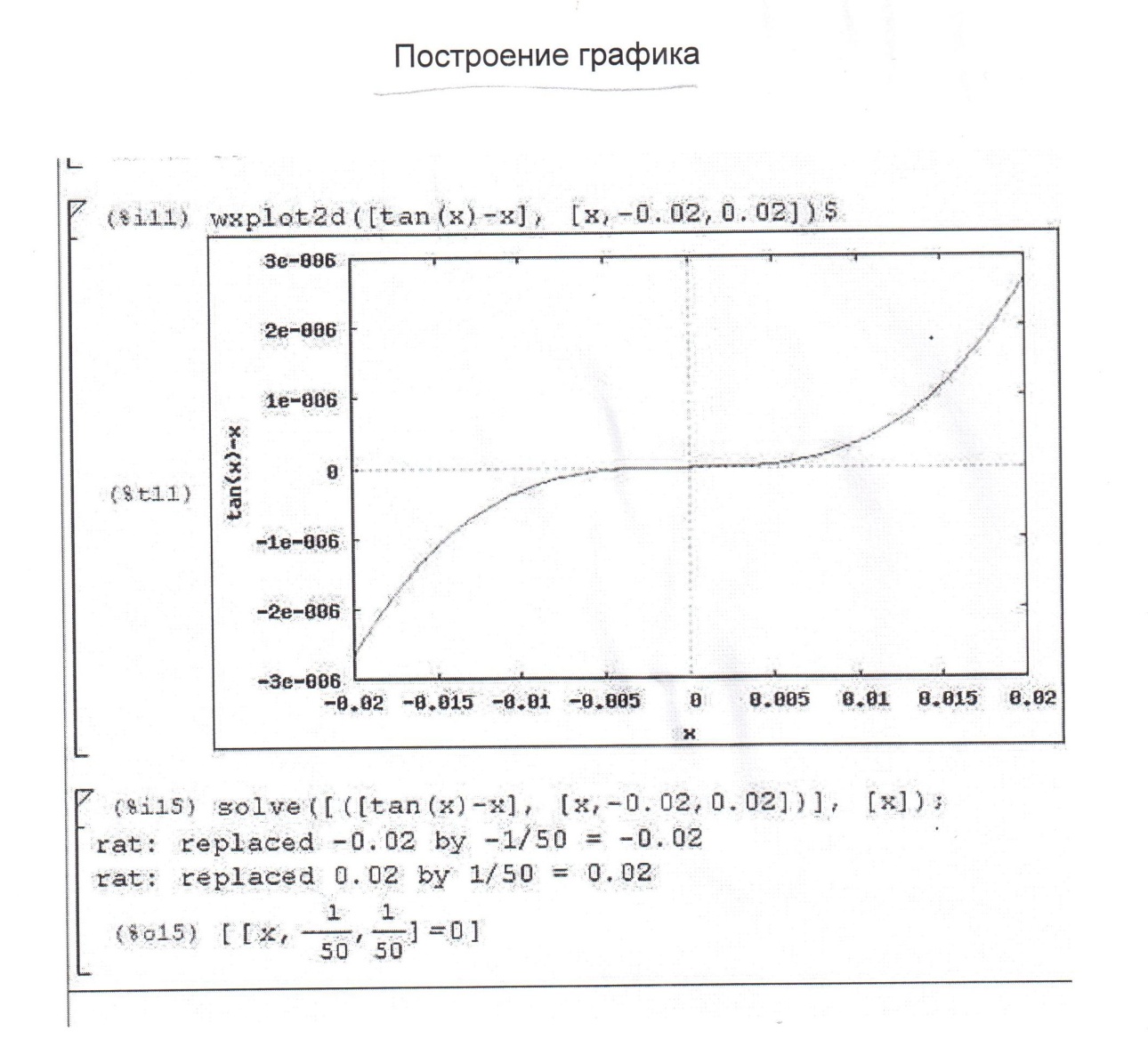
Рис 3.1

3.2 Текст программы.

REM

INPUT e

INPUT x2

IF ((tan(x2)-x2)*(1/cos(x2))^2-1))<0 GOTO 15

X3=x2-((tan(x2)-x2)/(1/cos(x2))^2-1)

IF ABS(x2-x3)<e THEN

GOTO 15

END IF

X1=X2

X2=X3

X3=X2-((tan(x2)-x2)*(x2-x3))-((tan(x2)-x2)-(tan(x1)-x1))

LOOP UNTIL ABS(x2-x3)<e

PRINT “x3=”;x3

Проверка предоставлена в пункте 5.

3.3 Результат работы программы.

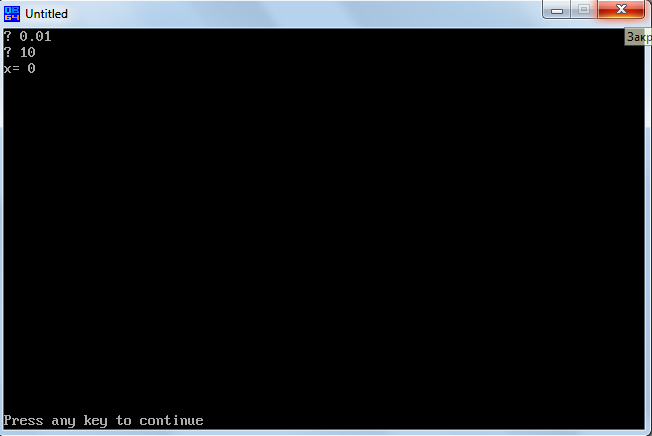
Рис 3.2

3.4 Алгоритм программы

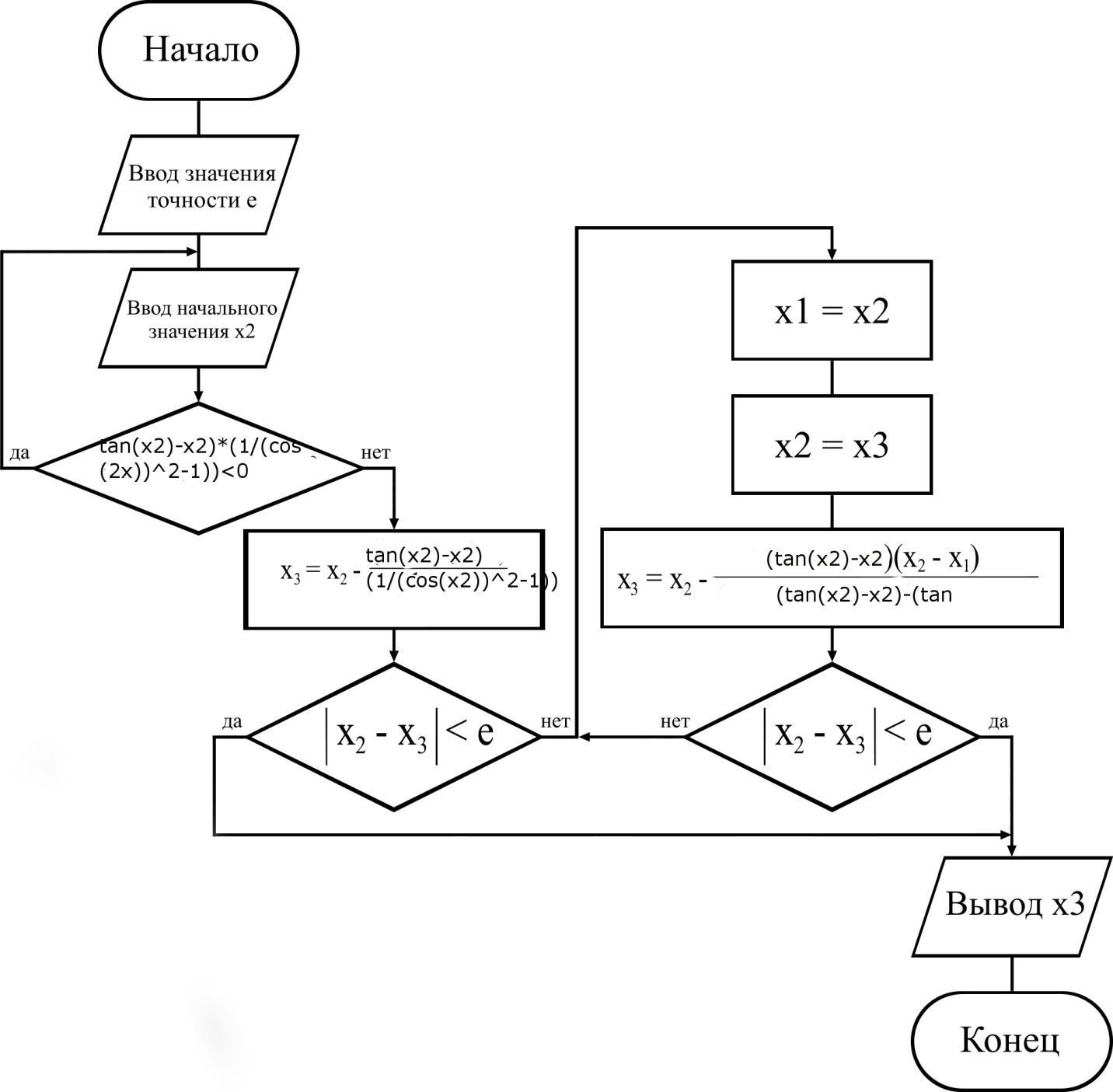
Рис. 3.3

4. Решение системы линейных алгебраических уравнений.

Реализовать программу на языке Q-Basic, которая производит вычисление корней системы линейных алгебраических уравнений (СЛАУ) методом Гаусса.

Исходная система:

21x1+3x2+4x3=20 x1+20x2+2x3=22 18x1+4x2+24x3=30

4.2. Описание метода

Метод Гаусса является одним из самых распространенных методов решения систем линейных уравнений. Этот метод еще называют методом последовательного исключения неизвестных.

Рассмотрим базовый вариант метода Гаусса, называемый схемой единственного деления.

ПРЯМОЙ ХОД состоит из n - 1 шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a₁₁ ( 0. Будем называть его главным элементом 1-го шага.

Найдем величины qi₁ = ai₁/a₁₁ (i = 2, 3, …, n), называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q₂₁, q₃₁, …, q_n1. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁ ,

a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a2n⁽¹⁾x_n = b₂⁽¹⁾ ,

a₃₂⁽¹⁾x₂ + a₃₃⁽¹⁾x₃ + … + a_3n⁽¹⁾x_n = b₃⁽¹⁾ ,

. . . . . . . .

a_n2⁽¹⁾x₂ + a_n3⁽¹⁾x₃ + … + a_nn⁽¹⁾x_n = b_n⁽¹⁾ .

в которой a_ij⁽¹⁾ и b_ij⁽¹⁾ вычисляются по формулам

a_ij⁽¹⁾ = a_ij - q_i1a_1j , b_i⁽¹⁾ = b_i - q_i1b₁.

2-й шаг. Целью этого шага является исключение неизвестного x₂ из уравнений с номерами i = 3, 4, …, n. Пусть a₂₂⁽¹⁾  0, где a₂₂⁽¹⁾ – коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага

q_i2 = a_i2⁽¹⁾ / a₂₂⁽¹⁾ (i = 3, 4, …, n)

и вычтем последовательно из третьего, четвертого, …, n-го уравнения системы второе уравнение, умноженное соответственно на q₃₂, q₄₂, …, q_n2. В результате получим систему

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a₁n_xn = b₁ ,

a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾ = b₂⁽¹⁾ ,

a₃₃⁽²⁾x₃ + … + a_3n⁽²⁾x_n = b₃⁽²⁾ ,

. . . . . . . . . . . . . . . . . .

. a_n3⁽²⁾x₃ + … + a_nn⁽²⁾x_n = b_n⁽²⁾ .

Здесь коэффициенты a_ij⁽²⁾ и b_ij⁽²⁾ вычисляются по формулам

a_ij⁽²⁾ = a_ij⁽¹⁾ – q_i2a_2j⁽¹⁾ , b_i⁽²⁾ = _bi⁽¹⁾ – q_i2b₂⁽¹⁾.

Аналогично проводятся остальные шаги. Опишем очередной r-й шаг.

r-й шаг. В предположении, что главный (ведущий) элемент r-го шага a_rr^(r–1) отличен от нуля, вычислим множители r-го шага

q_ir = a_ir^(r–1) / a_rr^(r–1) (i = r + 1, …, n)

и вычтем последовательно из (r + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы r-e уравнение, умноженное соответственно на q_r+1,r, q_r+2,r, …, q_nr.

После (n - 1)-го шага исключения получим систему уравнений

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁ ,

a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾x_n = b₂⁽¹⁾ ,

a₃₃⁽²⁾x₃ + … + a_3n⁽²⁾x_n = b₃⁽²⁾ ,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a_nn^(n–1)x_n = b_n^(n–1) .

матрица A(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

ОБРАТНЫЙ ХОД. Из последнего уравнения системы находим x_n. Подставляя найденное значение x_n в предпоследнее уравнение, получим x_n–1. Осуществляя обратную подстановку, далее последовательно находим x_n–1, x_n–2, …, x₁.

Вычисления неизвестных здесь проводятся по формулам

x_n = b_n(n–1) / a_nn(n–1),

x_r = (b_n(r–1) – a_r,r+1_(r–1)x_r+1 – … – a_rn(r–1)x_n) / a_r-1r-1, (r = n –1, …, 1).

Вычисление множителей, а также обратная подстановка требуют деления на главные элементы a_rr^(r–1). Поэтому если один из главных элементов оказывается равным нулю (или близким к нулю), то алгоритм не может быть реализован, необходимо принимать специальные меры.

i = 1,n,1

j = 1,n,1

i = 1,n,1