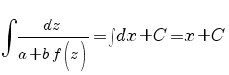4. Дифференциальные уравнения с разделенными переменными. Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним.

Уравнение вида

f1(x)dx=f2(y)dy,

называется уравнением с разделенными переменными.

Дифференциальное уравнение

называется уравнением с разделяющимися переменными.

Умножая обе части уравнения на , получаем уравнение

К разделяющимся переменным сводится уравнение вида:

Решение дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными

Делаем подстановку:

z = ax + by + c

где z - функция от х. Дифференцируем по x:

z' = a(x)′ + by′ + (c)′ = a·1 + by′ + 0 = a + by′

Подставляем:

Или:

Разделяем переменные - умножаем на dx, делим на (a + b·f(z)). При a + b·f(z) ≠ 0 получаем:

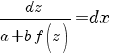
Интегрируем:

(1)

В заключение следует рассмотреть корни уравнения

a + b·f(z) = 0 ,

которые могут давать решения, не включенные в общий интеграл

5. Однородные дифференциальные уравнения первого порядка и приводящиеся к ним.

Функция f(x, y) называется однородной функцией n-го измерения относительно переменных х и у, если при любом справедливо тождество

Дифференциальное уравнение первого порядка называется однородным относительно х и у, если функция есть однородная функция нулевого измерения относительно х и у.

Решение однородного дифференциального уравнения.

Так как по условию . Положим , получим , т.е. однородная функция нулевого измерения зависит только от отношения аргументов. А само уравнение в этом случае примет вид .

Сделаем подстановку ; т.е. , тогда , подставим в исходное уравнение - это дифференциальное уравнение с разделяющимися переменными

Уравнение вида 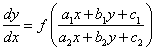(1) можно свести к однородному типу. Общий вид преобразований. Для того, чтобы привести уравнение (1) к однородному типу дифференциальных уравнений надо составить систему вида: 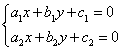Первый случай. Эта система имеет решение. Пусть решение этой системы : . Тогда, для приведения уравнения (1) к однородному типу необходимо сделать подстановку вида

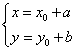
Второй случай. Напомним. Уравнение Приводим к однородному типу, составили систему , а решений эта система не имеет. В этом случае следует сделать замену .

6. Неоднородные линейные дифференциальные уравнения первого порядка. Решение неоднородного линейного дифференциального уравнения первого порядка методом Бернулли. Уравнения Бернулли.

Неоднородное дифференциальное уравнение — дифференциальное уравнение (обыкновенное или в частных производных), которое содержит тождественно не равный нулю свободный член — слагаемое, не зависящее от неизвестных функций.

Линейное уравнение первого порядка в стандартной записи имеет вид

Обыкновенное дифференциальное уравнение вида:

называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение).

Решение

Заменим

тогда:

Подберем так, чтобы было

для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определения получаем уравнение — уравнение с разделяющимися переменными.

7. Однородные и неоднородные линейные дифференциальные уравнения первого порядка методом вариации произвольной постоянной.

Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение — однородно, если .

В случае, если , говорят о неоднородном дифференциальном уравнении

Уравнение вида называется линейным неоднородным уравнением. Уравнение вида называется линейным однородным уравнением.

Очевидно, что однородное линейное уравнение является уравнением с разделяющимися переменными и его общее решение вычисляется по формуле 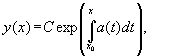где C— произвольная постоянная,

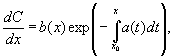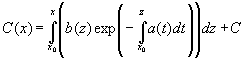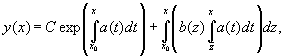Метод вариации произвольных постоянных для линейного неоднородного уравнения состоит в том, что решение неоднородного уравнения записывается в виде где C(x) неизвестная функция. Подставляя в уравнение имеем для C(x) откуда и тогда для общего решения неоднородного уравнения справедливо где C — произвольная постоянная.