Методы математической физики.

Вывод основных уравнений.

§1. Вывод уравнения колебания струны.

Рисунок 1

Пусть колебания

а) малые, т.е. угол между касательной к любой точке струны и осью много меньше единицы ( )

б) происходят в одной плоскости

Тогда, мы можем считать, что натяжение в любой точке струны постоянно ( ); т.к. , то

Выделим малый отрезок струны:

Рисунок 2

- линейная плотность

- сила, действующая на 1 метр струны

В проекции на ось :

Рисунок 3

Теорема Лагранжа

- уравнение Даламбера,

где - скорость распространения волны по струне.

Граничные условия:

Начальные условия:

§2. Вывод уравнения колебаний мембраны.

- сила на единицу площади

Рисунок 4

Выделим малый элемент мембраны:

Рисунок 5

Спроецируем силы на рис.5 на оси:

по теореме Лагранжа:

- скорость распространения волн по мембране

- волновое уравнение (уравнение Даламбера)

Начальные условия:

Граничные условия - мембрана закреплена, т.е. смещение равно нулю:

Частный случай:

Мембрана находится под действием силы тяжести, никаких колебаний нет.

Если мембрана является кругом, случай стационарный:

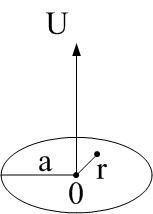
Рисунок 6

граничные условия:

- лапласиан

пусть ; применим граничные условия:

,

т.к. мембрана проседает; графиком является парабола.

§3. Вывод уравнения теплопроводности.

Рисунок 7

- объемная плотность

- удельная теплоемкость

- объемная плотность мощности

- вектор плотности потока тепла на единицу площади

Баланс тепла – все количество теплоты идет на увеличение температуры (нагрев) этого тела.

Выделим малый элемент этого тела:

Рассмотрим процесс в течение малого промежутка времени :

Рисунок 8

- количество тепла, выделившееся внутри объема за время за счет внутренних источников

- количество тепла, втекающего в тело вдоль оси 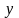с одной стороны

По теореме Лагранжа:

Полное приращение тепла внутри этого объема:

- приращение температуры

Закон Фурье:

Поток вектора плотности тепла прямопропорционален градиенту температуры

- поток направлен от более нагретым телам к менее нагретым

- коэффициент теплопроводности;

- уравнение Фурье

Начальное условие:

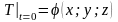
Конечные условия:

1) , где - точка поверхности

2)

3)охлаждение поверхности по закону Ньютона:

,

где - коэффициент пропорциональности

Если , то тепло вытекает из тела, т.е. его температура выше, чем у окружающей среды и наоборот.

Пусть процесс стационарен

- классическое уравнение Лапласа для стационарного распределения температуры.

§4. Вывод уравнения гидродинамики.

Жидкость идеальная, невязкая, т.е. будем рассматривать случай без трения.

Рисунок 9

- давление в жидкости;

- уравнение движения жидкости (II закон Ньютона в механике сплошных сред)

Рисунок 10

В этом случае - изменение скорости за время между I и II

- уравнение Эйлера (уравнение движения идеальной жидкости)

Уравнение неразрывности.

Уравнение неразрывности выражает собой закон сохранения массы.

Рисунок 11

- вектор плотности потока массы

- масса жидкости, втекающая в единицу объема за единицу времени

- закон сохранения массы

- уравнение адиабаты

§5.Безвихревое течение идеальной несжимаемой жидкости.

- безвихревое течение

- несжимаемая жидкость, тогда

,

где - потенциал

граничные условия:

а) на поверхности тела нормальная составляющая скорости

б)

§6. Малые возмущения жидкости.

Будем считать, что скорость мала, т.е. мы будем пренебрегать , то

где - возмущенное значение плотности (малое значение)

,

т.к. и - малые величины

- энтропия

, т.к. движение безвихревое, поэтому

- волновое уравнение

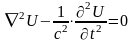- уравнение Даламбера

§7. Уравнение электростатики.

- теорема Гаусса-Остроградского

- I уравнение Максвелла

- уравнение Пуассона

Рисунок 12

граничные условия

Свойства уравнений математической физики.

§1. Классификация задач математической физики по виду добавочных условий.

I Краевая задача

Подставлены только граничные условия

Рисунок 13

Найти стационарное распределение температуры

- уравнение Лапласа

II Задача Коши

Даны только начальные условия

Рисунок 14

III Смешанная задача

Задаются начальные и граничные условия

Рисунок 15

§2.Классификация задач, связанных с уравнением Лапласа.

Решением уравнения Лапласа является гармоническая функция.

I Задача Дирихле

Требуется найти решение уравнения Лапласа, удовлетворяющие граничным условиям I рода.

т.е. на границе области задается сама функция.

II Задача Неймана

Требуется найти решение уравнения Лапласа, удовлетворяющее граничным условиям II рода.

т.е. должна быть задана производная по нормали, как функция в точке.

Функция не произвольная:

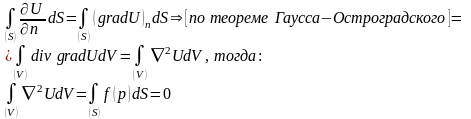
Ограничение на функцию - среднее значение этой функции на поверхности должно быть равно нулю, т.е. .

III Смешанная задача

Найти решение уравнения Лапласа, удовлетворяющее граничным условиям III рода

Пример задачи Коши:

Решение Даламбера о колебаниях неограниченной струны. Общее решение:

Введем новые переменные

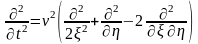
, где

:

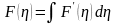
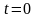Пусть , тогда

, т.е.: