
27(1). Интеграл Лебега.
f:ER, E(f>0)={xE: f(x)>0}
E(f>a)={xE: f(x)>a} (совокупность всех тех х из Е, где f(x)>a)
Опр.Функция f называется измеримой, если
1) Е – измеримо;
2) аR E(f>a) – измеримо.
Утв. Непрерывная функция на отрезке – измеримая функция.
Пусть f – измеримая ограниченная функция на измеримом ограниченном множестве Е. Существуют А и В такие, что Аf(x)В хЕ. Разобьем отрезок [А,В]: А=у0<y1<…<yn=B. Это разбиение обозначим через Т. Обозначим через ек=Е(ук-1fyk) k=1,2,…,n. Множества ек– измеримы, т.к. ек =Е(fyk-1)E(fyk).
Рассмотрим
множества еi
и ej
и ij,
для определенности будем считать, что
i<j.
Пусть х
еi
уi-1fyi
, если х
еj
уj-1fyj
уiyj
, т.е. f(x)уiyj
. Эти множества не пересекаются, т.е. еi
ej
=,
![]() , если к этому равенству применить
аддитивность, то получим
, если к этому равенству применить
аддитивность, то получим
![]() .
Возьмем параметр разбиения
.
Возьмем параметр разбиения
![]() .
Введем суммы Лебега: нижняя сумма
.
Введем суммы Лебега: нижняя сумма
![]() и верхняя
и верхняя
![]() .
Рассмотрим разность сумм
.
Рассмотрим разность сумм
![]()
![]()
Любая
нижняя сумма ограничена сверху некоторым
вещественным числом
![]() и u<S
и u<S
Любая
верхняя сумма ограничена снизу некоторым
вещественным числом
![]() и u<v
и u<v
suvS 0u-sv-sS-s, но S-smE0. Из неравенства uv 0v-u, т.к. Sv v-uS-uS-s . Перейдем к пределу при 0 получим 0v-u0 v-u=0 v=u.
Опр.
Интегралом Лебега функции f
по множеству Е называется общее значение
чисел u
и v
и обозначается
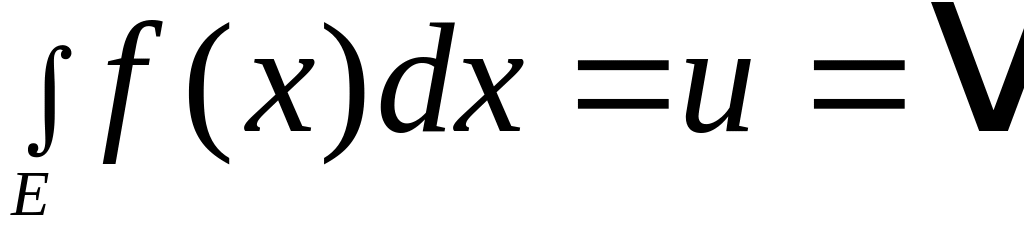 .
Интеграл определяется функцией f
множества E
и числами A
и B,
при этом он определен для всякой измеримой
ограниченной функции и он есть конечное
вещественное число
.
Интеграл определяется функцией f
множества E
и числами A
и B,
при этом он определен для всякой измеримой
ограниченной функции и он есть конечное
вещественное число
![]()
Теорема. (о среднем) Пусть на измеримом ограниченном множестве Е задана измеримая, ограниченная функция f, af(x)b, xE, тогда
![]()
Возьмем
nN,
![]() ,
,
![]() .
Тогда An<af(x)b<Bn
, An
и Bn
– верхняя и нижняя границы. An=у0<у1…уm=
Bn
. Строим по этому разбиению нижнюю сумму
.
Тогда An<af(x)b<Bn
, An
и Bn
– верхняя и нижняя границы. An=у0<у1…уm=
Bn
. Строим по этому разбиению нижнюю сумму
![]()
yk-1An
и yk-1Bn
тогда
![]()
![]() ,
т.к.
,
т.к.
![]() перейдем к пределу при 0
перейдем к пределу при 0
![]() далее перейдем к
пределу при n0
далее перейдем к
пределу при n0
![]() .
.
Опр. Те множества, которые находятся во взаимнооднозначном соответствии с N называется счетным. Множество всех целых чисел счетно.
Теорема (о полной аддит. интеграла Лебега).
Пусть
ограниченное измеримое множество Е
представлено в виде объединения попарно
не пересекаемых счетного или конечного
числа измеримых множеств Ек
, т.е.
![]() ЕiЕj=,ij.
Тогда
ЕiЕj=,ij.
Тогда
![]() .
.
Утв.(аддитивность относительно функции)
Пусть
на ограниченном измеримом множестве
заданы две измеримые ограниченные
функции f
и g.
Тогда
![]()
Утв.(монотонность)
Пусть на ограниченном измеримом множестве
Е заданы две измеримые ограниченные
функции f
и g
такие, что f
g
на Е. Тогда
![]() .
.
Теорема. Пусть на ограниченном измеримом множестве Е задана измеримая ограниченная функция f. Для того чтобы функция f была интегрируемой по Риману необходимо и достаточно, чтобы мера множества точек разрыва этой функции равнялась нулю.
Теорема. Если ограниченная измеримая функция f интегрируема по Риману, то эта функция интегрируема по Лебега, причем интегралы (в смысле Римана и в смысле Лебега) совпадают.
Обратное утверждение не верно.
