П. 2.2.Оценка погрешности

Получим выражение для погрешности квадратурной формулы интерполяционного типа. Представим функцию в виде

,

где - интерполяционный многочлен для , построенный по узлам .

- погрешность интерполирования.

Тогда получим

Таким образом, погрешность квадратурной формулы (2.2), (2.3) равна

(2.4)

где - погрешность интерполирования.

Для погрешности интерполирования была получена формула . Применив ее, получим

. (2.5)

Отсюда приходим к следующей оценке погрешности квадратурной формулы интерполяционного типа:

, (2.6)

где .

Из формулы (2.6) видно, что справедливо следующее утверждение:

Утверждение 2.1. Квадратурная формула интерполяционного типа, построенная по (n+1) узлу является точной для любого многочлена степени n и - коэффициенты, вычисленные согласно (2.3), то имеет место равенство

. (2.7)

Справедливо и обратное утверждение:

Утверждение 2.2. Если квадратурная формула точна для любого многочлена степени n, то она является квадратурной формулой интерполяционного типа.

§3.Квадратурные формулы наивысшей алгебраической степени точности

Рассмотрим следующую задачу: построить квадратурную формулу

, (3.1)

которая при заданном n была бы точна для алгебраического многочлена возможно большей степени.

Такие квадратурные формулы называются квадратурными формулами наивысшей алгебраической степени точности или формулами Гаусса. Эти формулы точны для любого алгебраического многочлена степени 2n-1.

Потребуем, чтобы квадратурная формула (3.1) была точна для любого алгебраического многочлена степени m. Это эквивалентно требованию, чтобы формула была точна для функции . Отсюда получаем условия

(3.2)

Они представляют собой нелинейную систему уравнений относительно неизвестных . Для того чтобы число уравнений равнялось числу неизвестных, надо потребовать .

Пример 1. Пусть , a=-1, b=1, n=1, m=1. Система (3.1) принимает вид

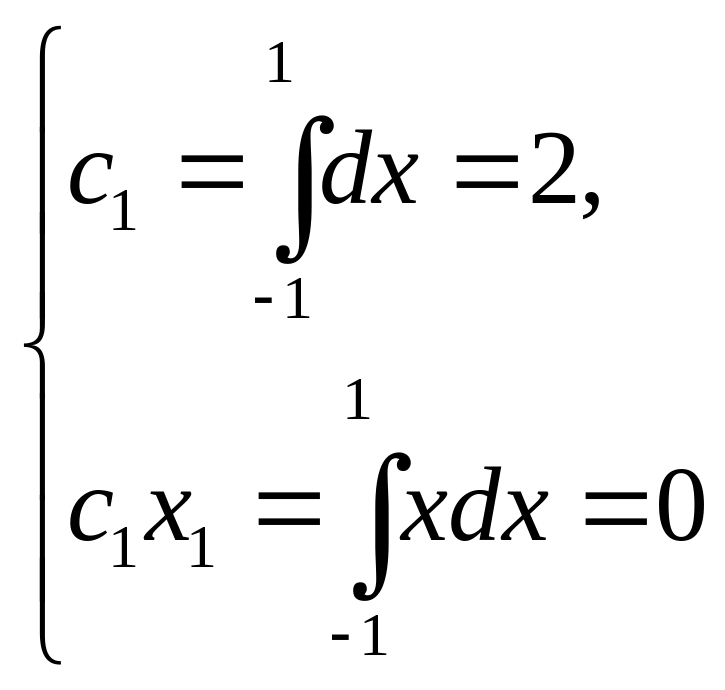
т.е. приходим к формуле прямоугольников: , которая точна для любого многочлена первой степени.

Пример 2. При n=2, m=3 система (3.2) записывается в виде

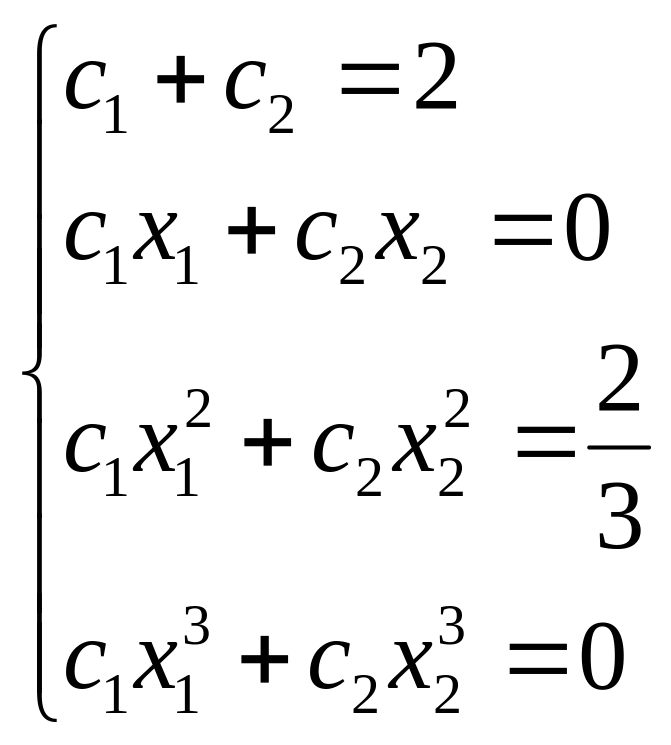
Отсюда находим , , т.е. получаем квадратурную формулу , которая точна для любого многочлена третьей степени.

Введем многочлен

(3.3)

Будем предполагать, что .

Теорема 3.1. Квадратурная формула (3.1) точна для любого многочлена степени тогда и только тогда, когда выполнены два условия:

1. многочлен 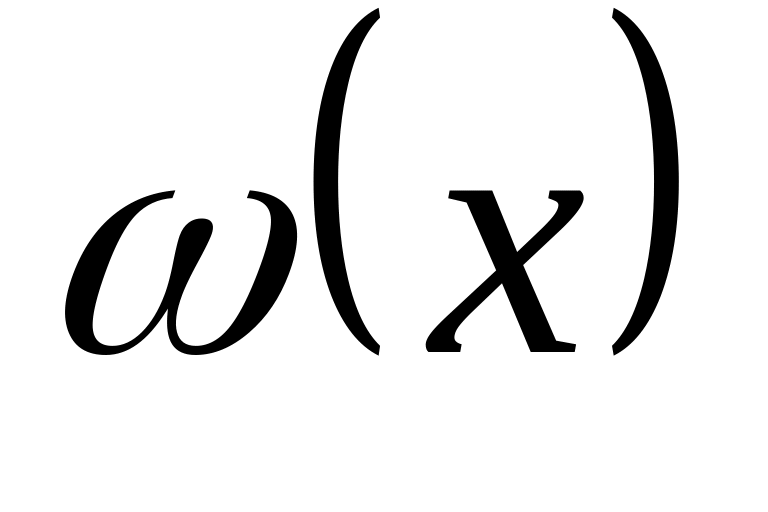ортогонален с весом 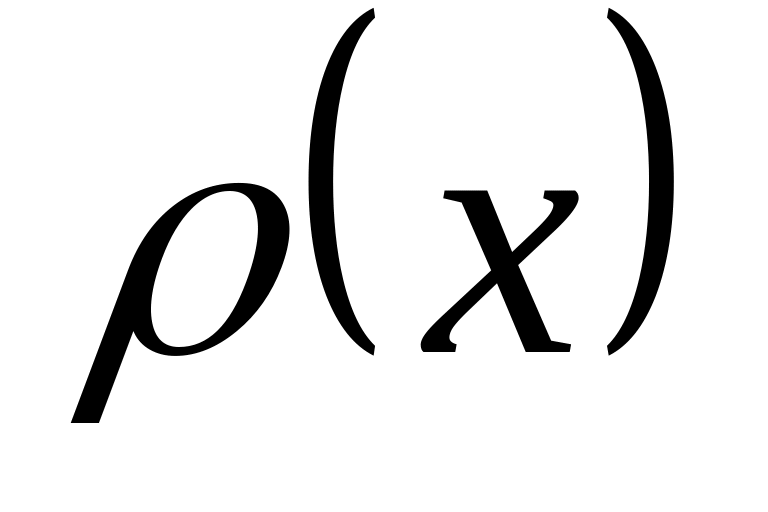любому многочлену 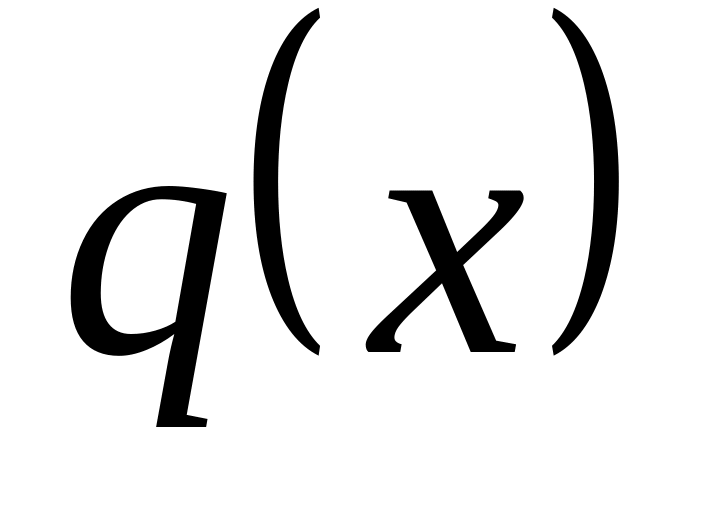степени меньше n, т.е.

(3.4)

2. Формула (3.1) является квадратурной формулой интерполяционного типа, т.е.

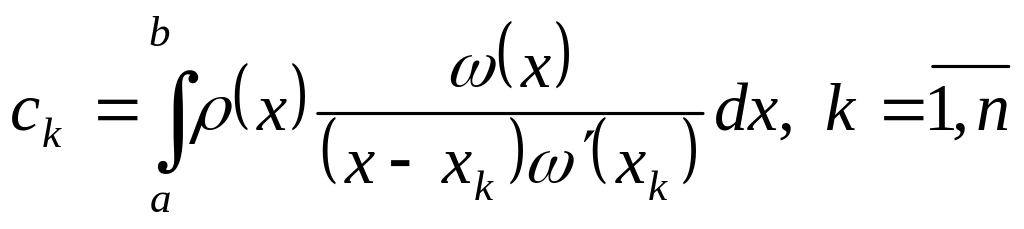(3.5)

Условие (3.4) эквивалентно требованиям

, (3.6)

которые представляют собой систему n уравнений относительно n, неизвестных .

Таким образом, для построения формул Гаусса достаточно найти узлы из соотношений ортогональности (3.6) и затем вычислить коэффициенты согласно (3.5).

Теорема 3.2. Если - многочлен степени n, ортогональный на с весом любому многочлену степени меньше n, то все его корни различны и расположены на .

Из теорем 3.1 и 3.2 следует, что для любого n существует, притом единственная квадратурная формула, точная для любого многочлена степени 2n-1.

Для погрешности формулы Гаусса справедливо представление

, (3.7)

где .

Рассмотрим частный случай:

Пусть . В этом случае в качестве узлов берутся нули многочлена Лежандра:

(3.8)

Свойства многочлена Лежандра:

1°.

2°. , - полином степени k.

3°. имеет n различных действительных корней принадлежащих интервалу .

Коэффициенты квадратурной формулы находятся из линейной системы:

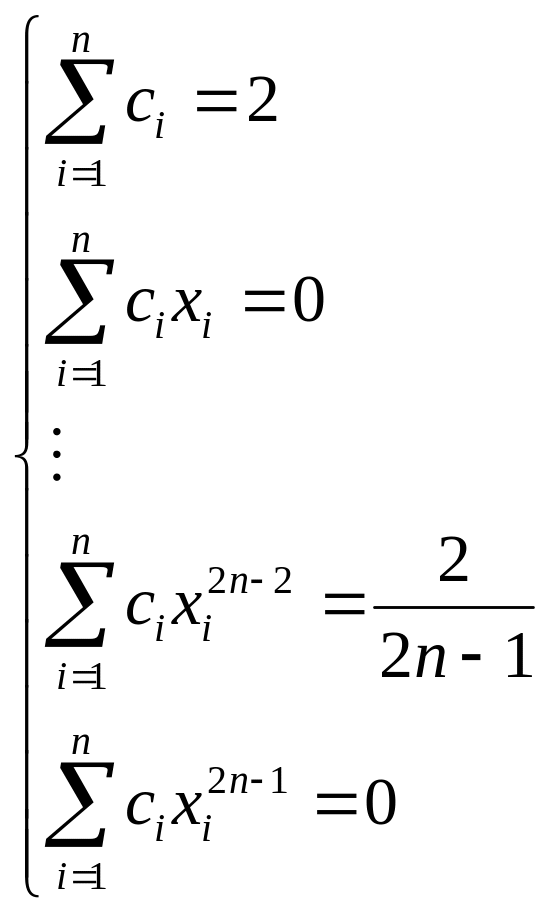(3.9)

Вычисления интеграла ведутся по следующим формулам

(3.10)

где (3.11)

- нули многочлена Лежандра.