5.1. Поиск локального минимума метом одномерной оптимизации

5.1.1 Метод дихотомии ( деление отрезка пополам ).

Основная идея метода состоит в том, что на каждой итерации вычисляются значения только в двух точках и . Точки и располагаются симметрично относительно середины текущего отрезка и разнесены между собой ровно на половину этого отрезка. Поэтому на каждой итерации в силу унимодальности функции из рассмотрения исключается ровно половина текущего отрезка поиска.

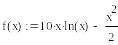
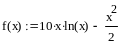
Проведем вычисление функции этим методом до тех пор пока длина уменьшаемого отрезка не станет меньше точности e=0.05, для этого потребуется примерно четыре итерации.

1:

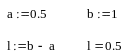
Найдем длину интервала

Выберем точки, равноотстоящие от концов заданного интервала

Теперь не обходимо вычислить значение функции в выбранных точках

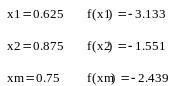
Как видно из вычисленных значений точка x1 является экстремумом из выбранных нами значений на этом шаге, а значит концом отрезка становиться середина, тем самым мы отсекаем половину отрезка, а бывшая точка x1 становиться серединой нового отрезка

Так как длина полученного отрезка после первой итерации больше е

то мы переходим ко второй итерации с новыми значениями, аналогично повторяя первую.

2:

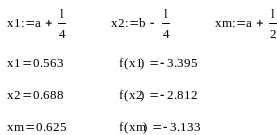
Условия окончания не выполнятся переходим к следующей итерации.

3:

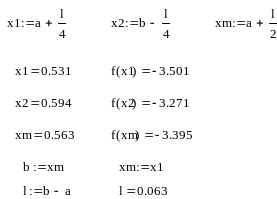
4:

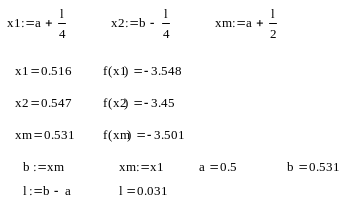
Полученное значение на этой итерации устраивает нас как экстремум функции вычисленный методом дихотомии, но для более точного вычисления экстремума продолжим решение этой задачи методом золотого сечения в следующем разделе.

Для более наглядного представления проделанных выше действий можно свести результаты в таблицу:

Шаг	Левая граница	Правая граница	Точка экстремума	Значение экстремума
1	0.5	1	0.625	-3.133
2	0.5	0.75	0.563	-3.395
3	0.5	0.625	0.531	-3.501
4	0.5	0.563	0.516	-3.548

4.3 Уточнение решения задачи Методом золотого сечения.

Алгоритм поиска экстремума функции f(x) на интервале [a₀; b₀] с использованием метода золотого сечения состоит из следующих шагов :

1. Задать a₀, b₀ – границы интервала поиска экстремума функции f(x);

 = 0.618 - константа.

2. Вычислить

и значение f(y₁), f(z₁).

3. Если f(y₁)  f(z₁), то положить a₁ = a, b₁ = z₁ и перейти к п. 4; иначе положить a₁ = y₁, b₁ = b₀ и перейти к п. 4.

4. Положить k = 1.

5. Если f(y_k)  f(z_k), то вычислить y_k+1 = a_k+b_k-y_k, f(y_k+1) и перейти к п.6; иначе положить y_k+1 = z_k, f(y_k+1) = f(z_k) и перейти к п. 7.

6. Положить z_k+1 = y_k, f(z_k+1) = f(y_k) и перейти к п. 8.

7. Вычислить z_k+1 = a_k+b_k-z_k, f(z_k+1) и перейти к п. 8.

8. Если f(y_k+1)  f(z_k+1), то положить a_k+1 = a_k, b_k+1 = z_k+1 и перейти к п.9; иначе положить a_k+1 = y_k+1, b_k+1 = b_k и перейти к п. 9.

9. Вычислить x^k = (a_k+1 + b_k+1) / 2.

10. Если k = 1, то перейти к п. 5; иначе перейти к п. 11.

11. Если | x^k-1 – x^k |  , то закончить поиск, иначе положить k = k+1 и перейти к п.5

Для нахождения экстремума этим методом используем отрезок [а,b], где а и b были найдены в предыдущем разделе на последнем этапе.

- вычислим по формуле , где l – длина нашего отрезка.

- будем писать как T).

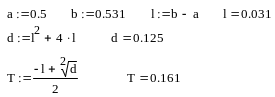
1:

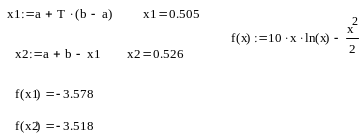
На 2-й итерации исходя из того что значение функции в точке x1 было меньше, конец отрезка b переноситься в точку x2, точка x1 остается прежней, и вычисляется новое значение точки x2.

2:

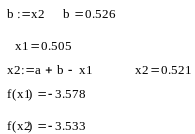
На предыдущей итерации f(x2)>f(x1), а следовательно необходимо снова перенести конец отрезка в точку x1.

3:

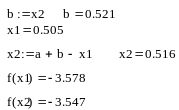
Аналогично проделываем еще две итерации для нахождения экстремума заданной функции.

4:

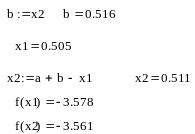
5:

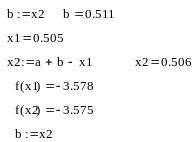
Вычисленный экстремум в точке x1 = 0.505 . Оставшийся отрезок :