
- •Часть II
- •Оглавление
- •Дидактический план
- •Литература*
- •Перечень умений
- •Тематический обзор*
- •1 Собственные числа и собственные векторы матрицы
- •1.1 Определение. Основные свойства собственных векторов
- •1.2 Характеристический многочлен
- •1.3 Собственное подпространство
- •2 Приведение симметричной матрицы к диагональному виду
- •2.1 Скалярное произведение в пространстве Rn. Процесс ортогонализации
- •2.2 Ортогональная матрица
- •2.3 Собственный базис симметричной матрицы
- •3 Квадратичная форма. Приведение к каноническому виду
- •3.1 Основные определения. Матрица квадратичной формы
- •3.2 Преобразование матрицы при линейной замене переменных
- •3.3 Приведение квадратичной формы к каноническому виду ортогональным преобразованием
- •3.4 Приведение кривой второго порядка к каноническому виду
- •3.5 Знакоопределенные квадратичные формы. Критерий Сильвестра
- •4 Линейные пространства
- •4.1 Определение линейного пространства
- •4.2 Линейная зависимость
- •4.3 Базис и координаты. Размерность пространства
- •4.4 Матрица перехода
- •4.5 Подпространство
- •4.6 Евклидовы пространства
- •3. Теорема Пифагора и ее обобщение.
- •5 Линейные операторы
- •5.1 Определение и примеры
- •5.2 Матрица линейного оператора
- •5.3 Самосопряженный оператор
- •Приложение 1 Перпендикуляр из точки на пространство
- •Приложение 2 о приближенном вычислении собственных значений матрицы
- •Задания для самостоятельной работы
- •1.Решите самостоятельно следующие задачи (номер варианта совпадает с вашим номером в списке группы):
- •Тренинг умений
- •1 Пример выполнения упражнения тренинга на умение № 1
- •2 Пример выполнения упражнения тренинга на умение № 2
- •3 Пример выполнения упражнения тренинга на умение № 3
- •4 Пример выполнения упражнения тренинга на умение № 4
- •5 Пример выполнения упражнения тренинга на умение № 5
- •6 Пример выполнения упражнения тренинга на умение № 6
- •7 Пример выполнения упражнения тренинга на умение № 7
- •8 Пример выполнения упражнения тренинга на умение № 8
- •9 Пример выполнения упражнения тренинга на умение № 9
- •10 Пример выполнения упражнения тренинга на умение № 10
- •11 Пример выполнения упражнения тренинга на умение № 11
- •12 Пример выполнения упражнения тренинга на умение № 12
- •13 Пример выполнения упражнения тренинга на умение № 13
- •Глоссарий
- •Линейная алгебра с элементами аналитической геометрии юнита 3
- •Часть II
3. Теорема Пифагора и ее обобщение.
Пусть х и у ортогональные векторы,
тогда
естественно считать диагональю
прямоугольника со сторонами х и у.
Покажем, что
![]() ,
т.е. что квадрат гипотенузы равен сумме
квадратов катетов.
,
т.е. что квадрат гипотенузы равен сумме
квадратов катетов.
Действительно, по определению
![]() .
Используя аксиомы 2, 1 и ортогональность
х и у, получаем
.
Используя аксиомы 2, 1 и ортогональность
х и у, получаем
![]() ,
,
что требовалось доказать.
Вообще, если
взаимно ортогональны и
![]() ,
то
,
то
![]() .
Если же х
и у
произвольные векторы, то по аналогии с
элементарной геометрией
– третья
сторона треугольника, построенного на
х
и у.
Используя неравенство Коши-Буняковского,
получаем
.
Если же х
и у
произвольные векторы, то по аналогии с
элементарной геометрией
– третья
сторона треугольника, построенного на
х
и у.
Используя неравенство Коши-Буняковского,
получаем
![]() ,
,
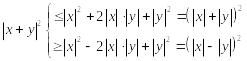 ,
,
т.е. длина любой стороны треугольника не больше, чем сумма длин двух других сторон и не меньше, чем модуль разности длин этих сторон.
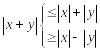 .
.
Расстоянием между
двумя точками х
и у
евклидова пространства называется
длина вектора
![]() :
:
![]() .
.
Ортогональный базис. В произвольном линейном пространстве не было оснований предпочитать одни базисы другим, там все базисы были равноправны. В евклидовом пространстве существуют более удобные базисы – ортогональные; они играют здесь ту же роль, что и прямоугольные системы координат в аналитической геометрии.
Мы докажем теперь теорему о существовании в произвольном евклидовом пространстве базиса из взаимноортогональных векторов. Более того, нас будет интересовать ортогональный нормированный базис, т.е. такой базис , в котором векторы попарно ортогональны и имеют каждый единичную длину
 .
(*)
.
(*)
Докажем лемму.
Лемма 1. Взаимно ортогональные
ненулевые векторы
![]() линейно независимы, т.е. что равенство
линейно независимы, т.е. что равенство
![]() (**)
(**)
возможно лишь при
![]() .
.
Действительно, умножим обе части равенства (**) скалярно на . Получим:
![]() .
.
Но по условию
![]() ,
,
![]() ,
при
,
при
![]() .
Следовательно
.
Следовательно
![]() .
Аналогично, умножая (**) скалярно на
,
получим
.
Аналогично, умножая (**) скалярно на
,
получим
![]() .
.
Теорема. Во всяком n-мерном евклидовом пространстве существует ортогональный нормированный базис.
Мы уже подробно рассматривали как строить ортогональную систему векторов в пространстве (процесс ортогонализации). Покажем для примера, как получить ортогональную систему функций в пространстве полиномов степени в .
Пусть
![]() .
Будем искать
.
Будем искать
![]() .
Из условия ортогональности
.
Из условия ортогональности
![]() и
и
![]() получаем
получаем
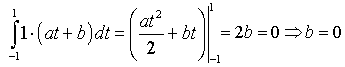 .
Потребуем, чтобы сумма коэффициентов
многочлена равнялась единице (что
равносильно равенству единице значения
многочлена при t=1).
.
Потребуем, чтобы сумма коэффициентов
многочлена равнялась единице (что
равносильно равенству единице значения
многочлена при t=1).
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пусть теперь
![]() .
Тогда
.
Тогда
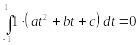 ,
,
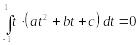 и
и
![]() .
.
Отсюда получим
![]() ,
,
,
,
![]() ,
и
,
и
![]() .
.
Получили ортогональную систему полиномов:
![]() ,
,
.
,
,
.
Действуя аналогично, можем получить
ортогональную систему многочленов
степени
при любом конечном n на отрезке
![]() .
.
Такую систему многочленов называют полиномами Лежандра. Полиномы Лежандра обладают многими замечательными свойствами и находят широкое применение в приложениях.
В евклидовом пространстве рассматривается
задача о проекции произвольного вектора
![]() на некоторое
подпространство W
V
и доказывается теорема о том, что каждый
вектор
может
быть разложен в прямую сумму двух
векторов, один из которых есть вектор
подпространства W,
а другой
принадлежит ортогональному дополнению
W. Подробнее об этой задаче можно
прочесть в Приложении.
на некоторое
подпространство W
V
и доказывается теорема о том, что каждый
вектор
может
быть разложен в прямую сумму двух
векторов, один из которых есть вектор
подпространства W,
а другой
принадлежит ортогональному дополнению
W. Подробнее об этой задаче можно
прочесть в Приложении.
