
- •1. Визначники 2-го та 3-го порядків визначаються наступним чином:
- •№29.Множина. Функції, послідовності, границя послідовностей.
- •№30.Границя функції.Основні теореми.
- •Основні теореми про границі функцій
- •1. Теорема РолляТеорема. Нехай функція задовольняє умовам:1) визначена і неперервна на відрізку 2) диференційована в інтервалі ;3) на кінцях відрізка набуває однакових значень: .
- •3. Теорема Коші
- •41. Застосування граничного аналізу при розв'язуванні задач оптимізації в економіці. Приклади.
- •Деякі властивості збіжних рядів
№1 Матриця, основні види матриць, дії з ними
Матрицею розміром m*n наз таблицю упорядкованих чисел або будь-яких інших об’єктів, розташованих в m рядках та n стовпцях.
Матриці
позначають великими літерами, наприклад
А, В,С та круглими дужками, а елементи
матриць позначають відповідними малими
літерами з 2-ма індексами, наприклад,
![]() .
.
Перший індекс i вказує номер рядка, в якому знаходиться цей елемент, а другий індекс j вказує номер стовпця, який містить цей елемент.
Так,
елемент ![]() знаходиться на перетині четвертого
рядка і третього стовпця матриці С.
знаходиться на перетині четвертого
рядка і третього стовпця матриці С.
Матриця розміру n*1 назив матрицею-стовпцем або вектором стовпцем. Мат розміру 1*n назив матрицею-рядком або вектором-рядком. Матрицею назив квадратною порядку n, якщо кіль-сть її рядків одинакова з кіль-стю стовпців і дорів n.Елементи квадратної матриці А порядку n , що розташовані на діагоналі матриці,яка проходить з лівого верхнього кута до правого нижнього кута, утвор головну діагональ матриці.Елементи квадратної матриці, що розташовані на головній діагоналі мат, яка проходить з правого верхнього кута долівого нижнього , утвор неголовну (допоміжну діагональ) матриці. Наприклад, в матриці
![]()
Елементами
головної діагоналі будуть: ![]() ,
а елемен-ми неголовної діагоналі будуть
,
а елемен-ми неголовної діагоналі будуть
![]() .
Квадратна
матриця назив діагональною, якщо всі
її елементи дорів 0, крім елементів
головної діагоналі.Діагональна матриця
всі елементи якої дорів 1 назив одиничною
мат-цею і познач Е.
.
Квадратна
матриця назив діагональною, якщо всі
її елементи дорів 0, крім елементів
головної діагоналі.Діагональна матриця
всі елементи якої дорів 1 назив одиничною
мат-цею і познач Е.
Мат-ці А і В назив рівними якщо
Вони мають однаковий розмір
Іхні
відповідні елементи рівні, тобто ![]() для всіх i
та j.
для всіх i
та j.
Якщо
в матриці А рядки записані стовпцями
їз збереженням їх нумерації, то одержана
матриця назив транспонованою і
позначається ![]() ,
а вказана операція перетворення матриці
назив транспонуванням мат-ці А.
,
а вказана операція перетворення матриці
назив транспонуванням мат-ці А.
Найпростішими діями з матрицями називають множення матриць на число, їх алгебраїчну суму та множення матриць.
Добутком матриці А на число к назив матриця, елементи якої дорівнюють добуткам відповідних елементів матриці А та число к:
![]()
Додавати та віднімати можна мат-ці лише однакового розміру.
Алгебраїчною
сумою матрицьА та В однакового розміру
m*n
назив матриця С розміру m*n,
елементи якої ![]() дорів такої самої алгебраїчної суми
елементів
дорів такої самої алгебраїчної суми
елементів ![]() та
та ![]() матриць А і В:
матриць А і В:
![]()
Добуток АВ матриць А і В існує лише при виконанні умов узгодженості:кількість стовпців матриці А (першого множника) дорів кі-сті рядків матриці В (2-го множника)
Добутком
АВ мат-ці А розміру m*n і матриці В розміру
n*p назив матриця С розміру m*p, елементи
якої дорівнюють сумі добутків елементів
і-го рядка матриці А на відповідні
елементи j-го стовпця матриці В. Таким
чином, кожен елемент матриці С знаходиться
за формулою:![]()
Ділення
матриці А/В розглядають як добуток
А*![]() ,
де
- матриця, обернена до матриці В.
,
де
- матриця, обернена до матриці В.
№6Матричний запис системи лінійних рівнянь і її розв’язування.
Розглянемо методи, придатні лише для розв’язання лінійних систем n-го порядку (n рівнянь із n невідомими):
Матричний метод розв’язування систем. Нехай матриця А невироджена(detA≠ 0), тоді існує обернена матриця A–1. Домножимо ліву і праву частини рівняння A ⋅X = B зліва на обернену матрицю A–1: (A−1A)X = A−1B⇔EX = A−1B. Оскільки EX = X, розв’язок системи A ⋅X = B набуде вигляду:X = A–1B.
Метод оберненої матриці зручно застосовувати для багаторазового розв’язування систем з однією і тією ж матрицею A і різними матрицями вільних членів B.
№2 Визначники другого та третього порядків та їх властивості
1. Визначники 2-го та 3-го порядків визначаються наступним чином:
![]()
![]()
Числа аj, bj, cj называются элементами определителя. Диагональ определителя, на которой расположены числа a1, b2 в случае (1) и a1, b2, c3 – в случае (2), называется главной. Элементы b1, a2 - в (1) и c1, b2, a3 – во (2) составляют побочную диагональ.
Для вычисления определителя второго порядка надо из произведения чисел, стоящих на его главной диагонали, вычесть произведение чисел, расположенных на побочной диагонали.
При вычислении определителей третьего порядка обычно пользуются правилом треугольников: первые три слагаемых с правой части равенства (2) вычисляются по схеме правилом треугольников: первые три слагаемых с правой части равенства (2) вычисляются по схеме І, они представляют собой произведения элементов, стоящих на главной диагонали и в вершинах двух треугонильков, у которых одна из сторон параллельна главной диагонали. Остальные три слагаемые правой части (2) вычисляются по аналогичной схеме ІІ, где за основу взята побочная диагональ. При этом произведения, вычисленные по второй схеме ставятся в формулу (2) с обратным знаком.
2. Свойства определителей.
І. При замене всех строк определителя на столбцы с теми же номерами величина его не изменяется (равноправность строк столбцов), т.е.
![]()
ІІ. При перестановке двух столбцов (или строк) определитель меняет свой знак
![]()
III. Умножение всех элементов какого-либо столбца (или строки) определяется на одно и то же число λ равносильно умножению на λ определителя. Иными словами, общий множитель всех элементов данного столбца (или строки) можно вынести за знак определителя
![]()
ІV. Если некоторый столбец (или строка) определителя целиком состоит из нулей, то определитель равен нулю.
V. если элементы какого-либо столбца определителя пропорциональны (в частности, равны) соответствующим элементам другого столбца, то определитель равен нулю. Аналогичное свойство верно и для строк. Так, определитель
![]()
так как элементы первых двух строк пропорциональны.
VІ. Если каждый элемент ƙ-го столбца (ƙ=1, 2 или 3) определителя представляет сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в том же столбце стоят первые слагаемые, а в другом – вторые. Остальные столбцы у обоих определителей одинаковые. Аналогичное свойство верно и для строк.
VІІ. Определитель не изменяется, если к элементам какого-либо столбца (или строки) прибавить соответственные элементы другого столбца (или строки), умноженные на любой общий множитель
![]()
VIII. Определитель равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
IХ. Сумма произведений элементов какого-либо столбца (строки) определителя на алгебраические дополнения соответственных элементов другого столбца (строки) равна нулю.
№3 Мінори та алгебраїчні доповнення
Дан визначник.
![]()
Мінором деякого елемента визначника називається визначник, який отримується з даного визначника викреслюванням строки та рядка, в яких цей елемент знаходиться.
Наприклад,
мінором елемента а1
визначника
є виз-к ![]() ,
мінором елемента в1
– виз-к
,
мінором елемента в1
– виз-к ![]() и т.д.
и т.д.
Алгебраїчним доповненням даного елемента визначника назив. Його мінором, який помножений на (-1)s s – сума номерів строки та стовпця, на перетині яких розміщений елемент. Алгебраїчне доповнення елементів першого рядка позначаються літерами А1,В1, С1, другого рядка – А2,В2,С2, третього рядка – А3,В3,С3.
Наприклад, елемент а1розташован на перетині першого стовпця і першого рядка, тому
А1=(-1)1+1![]()
Аналогічно,
В1=(-1)1+2![]()
Аналогічно виписуються і інші алгебраїчні доповнення. При цьому корисно мати на увазі наступну схему
![]()
Де знаками + або-відмічені місця тих елементів, для яких алгебраїчні доповнення рівні мінорам або відрізняються від них знаком.
№4Обернена матриця
Матриця А-1 називається оберненою до матриці А, якщо виконуються рівності
АА-1=А-1А=Е
Ці рівності означають, що мат-ця А та А-1 комутують і їх добуток є одиничною матрицею. Не кожна матриця має обернену обернену мат-цю. Мат-ця А має обернену матрицю лише при виконанні таких умов :
1.Матриця А є квадратною;
2.Визначник
![]() матриці А не дорівнює 0;
матриці А не дорівнює 0;
Якщо обернена матриця А-1 до матриці А існує, то її можна знаходити методом Гауса-Жордана або за формулою:
А-1=![]()
Де Аij – алгебраїчне доповнення елементів аij матриці А, причому алгебраїчне доповнення дддо елементів і-го рядка матриці А розташовані у і-тому стовпці.
№5 Системи лінійних рівнянь, їх сумісність, розв’язування методами Крамера, Гауса.
Система
m
лінійних
алгебраїчних рівнянь із n
невідомими
x1,
x2,
…, xnмає
вигляд: (2.1)де
aij−
задані
коефіцієнти при невідомих; bi−
вільні
члени системи. Систему можна записати
у матричній формі: A
⋅X
= B,
де A
–
матриця коефіцієнтів при невідомих; X
–
матриця-стовпець невідомих; B
–
матриця-стовпець вільних членів:
(2.1)де
aij−
задані
коефіцієнти при невідомих; bi−
вільні
члени системи. Систему можна записати
у матричній формі: A
⋅X
= B,
де A
–
матриця коефіцієнтів при невідомих; X
–
матриця-стовпець невідомих; B
–
матриця-стовпець вільних членів:
Розв’язком системи (2.1) називається впорядкована сукупність чисел x1, x2, …, xn, які перетворюють у правильну рівність кожне рівняння системи. Система називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку. Сумісна система називається визначеною, якщо вона має лише
один розв’язок і невизначеною, якщо вона має безліч розв’язків.
Метод Гаусса поєднує процес дослідження сумісності системи з процесом її розв’язання. Метод складається з прямого й зворотного ходу.
Прямий хід. Якщо a11 ≠ 0, то з першого рівняння системи виражають змінну x1 через інші змінні і підставляють у 2, 3,…, m-те рівняння. У результаті змінна x1 виключається з усіх рівнянь, крім першого. Потім із другого рівняння виражають змінну x2 через x3, x4, …, xnі підставляють у 3, 4,…, m-те рівняння. У результаті змінна x2 виключається з усіх рівнянь, крім першого та другого. Аналогічно виключають змінну x3 із 4, 5, …, m-го рівнянь і т.д.
Зворотний хід. З останнього рівняння системи визначається xnі підставляється в 1, 2, ..., (n − 1) рівняння. Потім із передостаннього рівняння визначається xn-1 і підставляється в 1, 2, ..., (n − 2)рівняння і т.д. Частинним розв’язком системи рівнянь називається розв’язок, в якому всім вільним невідомім задані конкретні числові значення.
Базисним розв’язком системи рівнянь називається розв’язок, в якому всі вільні невідомі дорівнюють нулю.
Теорема Крамера. Нехай Δ – визначник матриці А, Δj – визначник, отриманий з визначника Δ заміною j-го стовпця стовпцем вільних членів. Тоді при Δ ≠ 0 система має єдиний розв’язок: xj= Δj/Δ (j = 1, 2, …, n).
№7Власні значення і власні вектори матриці.
Нехай маємо квадратну матрицю A і матрицю (вектор)-стовпецьX:
A= X=
X=![]() Ненульовий
вектор X
називається
власним
вектором матриці
A,
якщо існує таке число λ
(власне
число матриці), що AX
=
λX.Матричне
рівняння
AX =
λX
запишемо у вигляді (A−λE)X
=
0.Для
того, щоб однорідна система (2.16) мала
ненульовий розв’язок, необхідно й
достатньо, щоб її визначник дорівнював
нулю.
Ненульовий
вектор X
називається
власним
вектором матриці
A,
якщо існує таке число λ
(власне
число матриці), що AX
=
λX.Матричне
рівняння
AX =
λX
запишемо у вигляді (A−λE)X
=
0.Для
того, щоб однорідна система (2.16) мала
ненульовий розв’язок, необхідно й
достатньо, щоб її визначник дорівнював
нулю.
Визначник det(A − λE) є многочленом степеня n відносно λ. Він називається характеристичним многочленом матриці А, рівняння det(A -λE)=0 − характеристичним рівнянням, а його корені – власними числами матриці А. Всього існує n власних чисел, серед котрих можуть бути рівні. Кожному власному числу відповідає свій власний вектор.
№8Приклади застосування матричного аналізу в економіці.
Балансовий метод. Балансові моделі широко застосовуються при математичному моделюванні економічних систем і процесів. В основі цих моделей лежить балансовий метод, тобто метод взаємного зіставлення наявних матеріальних, трудових і фінансових ресурсів і потреб у них. Під балансовою моделлю мається на увазі система рівнянь, кожне з яких виражає вимогубалансу між виробленою окремими економічними об’єктами кількістю
продукції і сукупною потребою в ній.
№9Вектори. Базис. Розкладання вектора за базисом.
Вектор AB – це напрямлений відрізок із початком у точці А і кінцем у точці В. Вектори позначаються як двома великими літерами,так і однією малою зі стрілкою: AB, a.
Вектор одиничної довжини називається одиничним вектором. Вектори, які лежать на одній прямій або на паралельних прямих,називаються колінеарними.Вектори, які паралельні одній площині, називаються компланарними.Вектори називаються рівними, якщо вони колінеарні, мають однакові довжини та однакові напрями.
Упорядкована
сукупність n
лінійно
незалежних векторів n-вимірного
простору утворює його базис.
Базисом
на прямій (у
R1)
називається будь-який ненульовий вектор.
Базисом
на площині (у
R2)
називаються два неколінеарні вектори,
взяті у визначеному порядку. Якщо кути
між базисними векторами довільні, базис
називають довільним
і
позначають базисні вектори ![]() 1,
2,
3.
Якщо базисні вектори взаємно перпендикулярні
(ортогональні), базис називають
ортогональним.
1,
2,
3.
Якщо базисні вектори взаємно перпендикулярні
(ортогональні), базис називають
ортогональним.
Якщо
вектор ![]() поданий у вигляді лінійної комбінації
базисних векторів:
=c1e1+c2e2+c3e3,
то кажуть, що він розкладений за базисом
1,
2,
3.
Вектори c1
1,
c2
2,
c3
3
називають складовими
(компонентами)
вектора
,
а числа c1,
c2,
c3
−
його
координатами
в
базисі
1,
2,
3.
Звичайно пишуть так:
=
(c1,
c2,
c3
).
поданий у вигляді лінійної комбінації
базисних векторів:
=c1e1+c2e2+c3e3,
то кажуть, що він розкладений за базисом
1,
2,
3.
Вектори c1
1,
c2
2,
c3
3
називають складовими
(компонентами)
вектора
,
а числа c1,
c2,
c3
−
його
координатами
в
базисі
1,
2,
3.
Звичайно пишуть так:
=
(c1,
c2,
c3
).
№12. Рівняння прямої з кутовим коефіцієнтом.
Всякая линия на плоскости определяется уравнением вида F(x,y)=0, где х и у –декартовы координаты произвольной точки этой линии. Они называются текущими координатами. В декартовых координатах каждая прямая определяется уравнением первой степени относительно х и у: Ах+Ву+С=0 и обратно, каждое уравнение Ах+Ву+С=0 определяет прямую. Это уравнение называется общим уравнением прямой.
Уравнение
прямой, разрешенное относительно у,
т.е. уравнение вида у=kx+b
называется уравнением прямой с угловым
коэффициентом, где k
– угловой коэффициент. Если
![]() -
угол, образованный прямой с положительным
направлением оси Ох (рис.1),
-
угол, образованный прямой с положительным
направлением оси Ох (рис.1),
 отсчитываемый
против часовой с трелки, то k=tg
.
Параметр b
называется начальной ординатой. Он
равен величине отрезка ОВ, отсекаемого
данной прямой на оси Оу, т.е. его длинне
взятой со знаком плюс, если точка В
находится выше оси Ох, и со знаком минус,
если – ниже. В частности, для прямых,
параллельных оси Ох, k=о,
и следовательно, их уравнение у= b.
Прямые, параллельные оси Оу, углового
коэффициента не имеют, т.к. для них
=900.
Поэтому такие прямые не могут быть
заданы уравнением у=kx+b.
Их уравнение имеет вид х=а, где а –
величина отрезка, отсекаемого прямой
на оси Ох.
отсчитываемый
против часовой с трелки, то k=tg
.
Параметр b
называется начальной ординатой. Он
равен величине отрезка ОВ, отсекаемого
данной прямой на оси Оу, т.е. его длинне
взятой со знаком плюс, если точка В
находится выше оси Ох, и со знаком минус,
если – ниже. В частности, для прямых,
параллельных оси Ох, k=о,
и следовательно, их уравнение у= b.
Прямые, параллельные оси Оу, углового
коэффициента не имеют, т.к. для них
=900.
Поэтому такие прямые не могут быть
заданы уравнением у=kx+b.
Их уравнение имеет вид х=а, где а –
величина отрезка, отсекаемого прямой
на оси Ох.
№10. Скалярний добуток векторів, його властивості та геометричне застосування.
Скалярним добутком двох векторів і називається добуток довжин цих векторів на косинус кута, утвореного векторами, тобто
![]() (1).
(1).
Скалярний добуток двох векторів дорівнює добутку довжини одного з них на проекцію іншого на напрям першого.
Основні властивості:

 -
випливає зразу з означення .
-
випливає зразу з означення .

Скалярний квадрат вектора ā дорівнює квадрату його довжини, тобто ā2= ā*ā= |ā|2.
Перші три властивості показують, що при скалярному перемноженні суми векторів на суму вчиняють за звичайним правилом множення многочленів.
Властивість
4 вказує геометричний зміст знака
скалярного добутку. Із властивості 5
витікає формула: |ā|=![]() .
(2)
.
(2)
Якщо
відомий скалярний добуток векторів, то
за формулою (2) знаходяться їх довжини,
а з формули (1):
![]() .
(3).
.
(3).
Геометричний
зміст скалярного добутку: скалярний
добуток вектора ā
на одиничний вектор![]() дорівнює
проекції ā
на напрямок, який визначається
,
тобто:
дорівнює
проекції ā
на напрямок, який визначається
,
тобто:
![]() .
.
В
случае произвольного вектора
![]() :
:
![]() .
.
Механический
смысл скалярного произведения: скалярное
произведение силы
![]() на
вектор
на
вектор
![]() равно
работе W
этой силы при перемещении материальной
точки по вектору
,
т. е.: W=
.
равно
работе W
этой силы при перемещении материальной
точки по вектору
,
т. е.: W=
.
Из
определения скалярного произведения
вытекает следующая таблица умножения
![]() ,
,![]() ,
,![]() :
:
= =0, = =0, = =0, =1, =1, =1. (4)
Если
векторы даны своими координатами:
![]() ,
т.
е.
,
т.
е.
![]() ,
то переможая эти векторы скалярно и
используя формулы (4) получим выражения
скалярного произведения через координаты
векторов
,
то переможая эти векторы скалярно и
используя формулы (4) получим выражения
скалярного произведения через координаты
векторов
![]() .
.
№11. Векторний, мішаний добуток векторів, його властивості та геометричне застосування.
Векторным
произведением вектора ā
на вектор
называется такой третий вектор
|![]() |,
длинна и направление которого определяются
условиями:
|,
длинна и направление которого определяются
условиями:
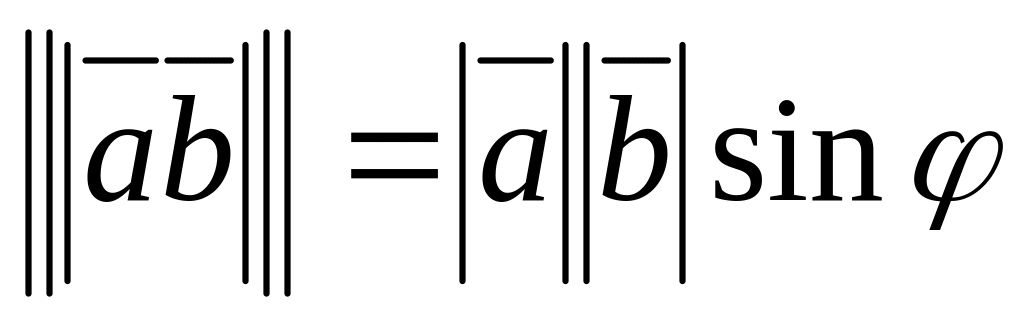 ,
где
-
угол между ā
и
;
,
где
-
угол между ā
и
; перпендикулярен
каждому из векторов ā
и
;
перпендикулярен
каждому из векторов ā
и
;направлен так, что кратчайший поворот от ā к виден с его конца совершающимся против часовой стрелки:
 рис.1.
рис.1.
Векторное произведение обладает следующими свойствами:



Векторное произведение равно нулю (нуль-вектору) тогда и только тогда, когда ā и коллинеарны. В частности,
 для
любого вектора ā.
для
любого вектора ā.Если ā и неколлинеарны, то модуль векторного произведения равен площади S построенного на них параллелограмма (рис.1).
Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов. Надо только следить за тем, чтобы порядок следования множителей не менялся.
Механический
смысл векторного произведения: если
- сила, приложенная к точке М,
то момент
![]() этой силы относительно точки А равен
векторному произведению векторов
этой силы относительно точки А равен
векторному произведению векторов
![]() и
,
т. е.
и
,
т. е.
![]() .
.
В
частности, момент относительно начала
координат
![]() ,
где r
– радиус-вектор точки приложения силы.
,
где r
– радиус-вектор точки приложения силы.
Основные
орты перемножаются следующим образом:
![]() ,
,
![]() .
.
Если:
![]() ,
то
,
то
![]()
Смешанное произведение трех векторов
Смешанным
произведением
![]() трех векторов называется их
векторно-скалярное произведение
трех векторов называется их
векторно-скалярное произведение
![]() .
.
Тройка
некомпланарных векторов
![]() ,
и
,
и
![]() называется правой, если кратчайшее
вращение от
к
видно с конца вектора
совершающимся против часовой стрелки,
и левой – если по часовой стрелке
(рис.1):
называется правой, если кратчайшее
вращение от
к
видно с конца вектора
совершающимся против часовой стрелки,
и левой – если по часовой стрелке
(рис.1):
 рис.1.
рис.1.
Геометрический смысл смешанного произведения:
Необходимым и достаточным условием компланарности трех векторов , и является равенство
 .
.Если некомпланарные векторы , и приведены к общему началу, то модуль смешанного произведения равен обьему параллелепипеда, построенного на , и . Если >0, то тройка векторов , и правая, если <0, то левая. Если векторы , и заданы своими координатами
 ,
то
,
то

Т.е. смешанное произведение равно определителю из координат сомножителей.
№13Рівняння прямої, яка проходить через дві задані точки.
Предположим,
что прямая проходит через точки А(х1,
у1)
и В(х2,
у2).
Если абсциссы и ординаты этих точек
различны, т.е. х1≠х2
и у1≠у2,
то уравнение прямой АВ имеет вид:
![]() .
Если абсциссы точек А и В одинаковы, то
прямая АВ параллельна оси ординат и
уравнение ее имеет вид х=х1.
.
Если абсциссы точек А и В одинаковы, то
прямая АВ параллельна оси ординат и
уравнение ее имеет вид х=х1.
При равенстве ординат точек А и В прямая АВ параллельна оси обсцисс и ее уравнение у=у1.
Пусть
прямая АВ представляется уравнением
и точка С(х3,
у3)
лежит на этой прямой, тогда ее координаты
удовлетворяют уравненю
,
т. е.
![]() .
.
Это
условие того, что три точки А(х1,
у1),
В(х2,
у2),
С(х3,
у3)
лежат на одной прямой. Предположим, в
частности, что прямая проходит через
точки А и В, лежащие на осях координат:
А(а, 0) и В(0, b),
тогда уравнение ее примет вид
![]() .
Это уравнение называется уравнением в
отрезках, так как а и b
представляют собой величины отрезков,
отсекаемыъ прямой на осях координат. К
такому виду может быть приведено
уравнение любой прямой, не проходящей
через начало координат и не параллельной
координатным осям.
.
Это уравнение называется уравнением в
отрезках, так как а и b
представляют собой величины отрезков,
отсекаемыъ прямой на осях координат. К
такому виду может быть приведено
уравнение любой прямой, не проходящей
через начало координат и не параллельной
координатным осям.
№15 Рівняння прямої, що проходить через дану точку перпендикулярно даній прямій
Означення. Пряма, що проходить через точку М1(х1, у1) і перпендикулярна до прямої у = kx + b зображується рівнянням: )(111xxkyy
Відстань від точки до прямої Теорема. Якщо задана точка М(х0, у0), то відстань до прямої Ах + Ву + С =0 визначається як . 2200BACByAxd
№ 16 Кут між прямими на площині
Означення. Якщо задані дві прямі y = k1x + b1, y = k2x + b2, то гострий кут між цими прямими буде визначатись як . Дві прямі паралельні, якщо k1 = k2. Дві прямі перпендикулярні, якщо k1 = -1/k2. Теорема. Прямі Ах + Ву + С = 0 і А1х + В1у + С1 = 0 паралельні, коли пропорційні коефіцієнти А1 = А, В1 = В. Якщо ж і С1 = С, то прямі співпадають. Координати точки перетину двох прямих знаходяться як розв‟язок системи рівнянь цих прямих.
№17.Нормальне рівняння прямої відстань від точки до прямої.
Нормальне рівняння прямої x cosα + y sinα p = 0, де р – відстань від початку координат до прямої, n0(cosα, sіnα) – одиничний вектор нормалі прямої.Нормальне рівняння площини у просторіПозначимо через ` n вектор один.. Якщо Пл-на прох. Через поч. Коорд, то можна взяти будь-який вектор одиночної довжинОА=(x,y,z)ОА=Р ( ` n, ` ОА)=Р. Позначимо кути які утв. ` n з коорд. Осями ` n=(cos a , cos b , cos c ). Тоді нормальне рівняння площини у просторі xcos a + ycos b + z cos c - P=0.Відстань від точки до прямої Нехай пряма задана рівнянням і точка радіус-вектор якої направляючий вектор прямої Тоді відстань від точки до прямої можна розглядати як висоту паралелограма, побудованого на векторах
№ 14 Рівняння прямої у відрізках
Рівняння першого степеня, що зв'язує координати точки на площині, - це рівняння
(3.3)
при умові
В декартовій системі координат на площині кожна пряма лінія може бути задана лінійним рівнянням і, навпаки, кожне лінійне рівняння (3.3) визначає пряму лінію .
Рівняння (3.3) називається загальним рівнянням прямої на площині.
Нехай точка лежить на прямій ( ). Це значить, що її координати задовольняють рівняння (3.7)
Вираховуючи із рівняння (3.7) дану рівність, одержимо рівняння прямої, що проходить через задану точку
(3.4)
Якщо довільна точка на прямій, то вектор повністю лежить на прямій а ліва частина рівності (3.8) виражає скалярний добуток векторів і Оскільки скалярний добуток цих векторів дорівнює нулю, то вони є перпендикулярні , а це значить, що вектор перпендикулярний прямій . Вектор, який перпендикулярний до прямої називається нормальним вектором прямої. Вектор який паралельний прямій, називається направляючим вектором прямої. Очевидно, що і, наприклад,
Нехай задана пряма Позначимо через радіус-вектор її початкової точки . Розглянемо тепер деяку точку , радіус-вектор якої позначимо через (рис.3.7). Вектор , початок якого лежить на прямій, паралельний прямій тоді і тільки тоді, коли його кінець ( точка ) також лежить на прямій. В цьому
Рис.3.7
випадку для точки знайдеться таке число (параметр), що
(3.5)
Рівняння (3.5) називається векторно-параметричим рівнянням прямої.
Нехай в загальному вигляді направляючий вектор має координати Записавши рівняння (3.5) в координатній формі, одержимо параметричні рівняння прямої на площині
(3.6)
Виключаючи із рівнянь (3.6) параметр одержимо канонічне рівняння прямої (3.7)
Із рівняння (3.17) одержимо
Позначимо . Тоді одержимо рівняння прямої, що проходить через задану точку в заданому напрямку
(3.8)
Очевидно, що де кут, що утворює пряма (вектор ) з
додатнім напрямом осі Величину називають кутовим коефіцієнтом прямої
Позначивши через із рівняння (3.8) одержимо рівняння прямої з кутовим коефіцієнтом
(3.9)
Нехай дві точки і лежать на прямій Тоді за напрямний вектор можна взяти вектор, що з'єднує ці дві точки Підставивши в рівняння (3.7)
Замість і координати вектора одержимо рівняння прямої, що проходить через дві заданих точки
(3.10)
Нехай задані точки перетину прямої з осями координат і Використавши рівняння (3.10), одержимо
або
(3.11)
Рівняння (3.11) називається рівнянням прямої у відрізках.
Рівняння прямої у відрізках на осях
Якщо в загальному рівнянні прямої Ах + Ву + С = 0 С 0, то, поділивши на –С, отримаємо:або , де Геометричний зміст коефіцієнтів в тому, що коефіцієнт а є координатою точки перетину прямої з віссю Ох, а b – координатою точки перетину прямої з віссю Оу. 1уСВхСА 1byaxBCbACa;
№18.Рівняння
площини, що проходить через точку
M(x0,y0,z0)
перпендикулярно
до вектора
![]() :
:
A(x − x0) + B(y − y0) + C(z − z0) = 0;
у векторній формі:
![]()
№19.Рівняння площини у відрізках на осях.
Рівняння площини у відрізках:
![]()
де a = − D / A,b = − D / B,c = − D / C — відрізки, які площина відсікає на осях Ox,Oy і Oz.
№20.Нормальне рівняння площини.Відстань від точки до площини.
Нормальне (нормоване) рівняння площини
![]()
у векторній формі:
![]()
де
![]() -
одиничний
вектор,
p —
відстань від площини до початку координат.
Рівняння(2) можна отримати з рівняння
(1), помноживши його на нормуючий множник
-
одиничний
вектор,
p —
відстань від площини до початку координат.
Рівняння(2) можна отримати з рівняння
(1), помноживши його на нормуючий множник
![]()
(знаки μ і D протилежні).
№21.Кут між двома площинами
Кут між площинами

Якщо у векторній формі, то
![]()
№23.Рівняння прямої лінії в просторі, що проходить через дві задані точки
Нехай
відомі координати двох різних точок
простору
![]() та
та
![]() ,
що належать деякій прямій
,
що належать деякій прямій
![]() .
Тоді у канонічному рівнянні
.
Тоді у канонічному рівнянні
![]() за
напрямний вектор візьмемо вектор
за
напрямний вектор візьмемо вектор
![]() ,
а за точку
,
а за точку
![]() ,
наприклад, точку
,
наприклад, точку
![]() .
Рівняння (1.3) набуде вигляду
.
Рівняння (1.3) набуде вигляду
![]() Дане Рівняння називається рівнянням
прямої лінії, що проходить через дві
задані точки
Дане Рівняння називається рівнянням
прямої лінії, що проходить через дві
задані точки
№24.Умова паралельності і перпендикулярності прямих в просторі
Условия
параллельности и перпендикулярности
двух прямых равносильны условиям
параллельности и перпендикулярности
их направляющих векторов
![]() и
и
![]() :
:
Две
прямые параллельны
тогда и только
тогда, когда их соответствующие
коэффициенты пропорциональны, т.е. l1
параллельна l2
тогда и только тогда, когда
![]() параллелен
параллелен
![]() .
.
Две
прямые перпендикулярны тогда и только
тогда, когда сумма произведений
соответствующих коэффициентов равна
нулю:
![]() .
.
№22.Параметричне рівняння прямої в просторі.Канонічне рівняння прямої в просторі.
. Дане
Рівняння називається канонічним
рівнянням прямої в просторі.
Зауважимо, що в рівнянні одне або два з
чисел
![]() можуть
дорівнювати нулю. Тоді напрямний вектор
q,
а, отже, і пряма
,
будуть паралельними до координатних
площин або координатних осей.
Зведення
загального рівняння прямої до канонічного
вигляду.
Нехай пряма лінія
в
просторі задана загальним рівнянням,
тобто є перетином двох різних непаралельних
площин
можуть
дорівнювати нулю. Тоді напрямний вектор
q,
а, отже, і пряма
,
будуть паралельними до координатних
площин або координатних осей.
Зведення
загального рівняння прямої до канонічного
вигляду.
Нехай пряма лінія
в
просторі задана загальним рівнянням,
тобто є перетином двох різних непаралельних
площин
![]() . Для
того, щоб звести рівняння прямої до
канонічного вигляду (1.2), треба знайти:
1)
хоча б одну точку
. Для
того, щоб звести рівняння прямої до
канонічного вигляду (1.2), треба знайти:
1)
хоча б одну точку
![]() ,
що належить прямій
2) напрямний вектор
,
що належить прямій
2) напрямний вектор
![]() прямої
Оскільки система має безліч розв'язків,
то надамо змінній
прямої
Оскільки система має безліч розв'язків,
то надамо змінній
![]() довільного
числового значення
довільного
числового значення
![]() ,
тоді отримаємо систему двох лінійних
рівнянь щодо невідомих
,
тоді отримаємо систему двох лінійних
рівнянь щодо невідомих
![]()
![]() . Із
системи за формулами Крамера, знаходимо
однозначні розв'язки
. Із
системи за формулами Крамера, знаходимо
однозначні розв'язки
![]() ,
що відповідають значенню
,
що відповідають значенню
![]()
![]() де
визначники
де
визначники
![]() ,
,
![]() .
Отже,
числа
.
Отже,
числа
![]() ,
що є розв'язками системи, будуть
координатами точки
,
що належить прямій
Знайдемо тепер
компоненти напрямного вектора
,
що є розв'язками системи, будуть
координатами точки
,
що належить прямій
Знайдемо тепер
компоненти напрямного вектора
![]() .
Вектор
q буде
ортогональним до кожного з нормальних
векторів
.
Вектор
q буде
ортогональним до кожного з нормальних
векторів
![]() та
та
![]() площин
площин
![]() та
та
![]() відповідно.
Тому вектор q можна
знайти як векторний добуток векторів
відповідно.
Тому вектор q можна
знайти як векторний добуток векторів
![]() та
та
![]()

![]() Отже, компоненти напрямного вектора
прямої
Отже, компоненти напрямного вектора
прямої
![]()
![]()
![]() .
.
Параметричне
рівняння прямої лінії в просторі можна
отримати із канонічного рівняння прямої,
якщо прирівняти до параметра
![]() кожне
із співвідношень
кожне
із співвідношень
![]() .
(1.7)
Оскільки
один із знаменників у співвідношенні
(1.7) відмінний від нуля, а відповідний
чисельник може набувати довільних
значень, то областю зміни параметра
є
вся числова вісь. Із рівностей (1.7)
визначимо
.
(1.7)
Оскільки
один із знаменників у співвідношенні
(1.7) відмінний від нуля, а відповідний
чисельник може набувати довільних
значень, то областю зміни параметра
є
вся числова вісь. Із рівностей (1.7)
визначимо
![]()
 .,
tЄ R
(1.8)
Рівняння (1.8) називається
параметричним
рівнянням прямої
в просторі.
.,
tЄ R
(1.8)
Рівняння (1.8) називається
параметричним
рівнянням прямої
в просторі.
№25. Кут між прямою і площиною. Умови перпендикулярності і паралельності прямої та площини
Кутом
між прямою та площиною
називається кут між цією прямою і її
проекцію (ортогональною)
на площину.
Якщо пряма перпендикулярна
до площини, то кут між нею й площиною
вважається таким, що дорівнює
![]() ,
а між паралельними прямою та площиною
таким, що дорівнює
,
а між паралельними прямою та площиною
таким, що дорівнює
![]() .
Кут
між прямою та площиною і кут між цією
прямою й перпендикуляром до площини в
сумі дорівнюють
.
На
рисунку
.
Кут
між прямою та площиною і кут між цією
прямою й перпендикуляром до площини в
сумі дорівнюють
.
На
рисунку
![]() .
.

Теорема
1. Якщо пряма, яка не належить площині,
паралельна якій-небудь прямій у цій
площині, то вона паралельна
і самій площині.
Теорема
2. Якщо пряма паралельна площині, то на
цій площині знайдеться пряма, яка
паралельна даній прямій.
Зверніть
увагу: паралельність прямої і площини
не означає, що ця пряма паралельна
будь-якій прямій на цій площині. Кожна
пряма цієї площини буде або паралельна
даній, або мимобіжна з нею.
![]() На
рисунку:
На
рисунку:
![]() ;
;
![]() ;
;
![]() ;
a
і b
— мимобіжні;
;
a
і b
— мимобіжні;
![]() .
Теорема
3. Через точку, що не лежить на площині,
можна провести безліч прямих, паралельних
даній площині, причому всі вони лежать
в одній площині (паралельній даній).
.
Теорема
3. Через точку, що не лежить на площині,
можна провести безліч прямих, паралельних
даній площині, причому всі вони лежать
в одній площині (паралельній даній).
Пряма,
яка перетинає площину, називається
перпендикулярною
до цієї площини,
якщо вона перпендикулярна до будь-якої
прямої, що лежить у цій площині й проходить
через точку перетину (див. рисунок).
![]() Теорема
3. Якщо пряма перпендикулярна до двох
прямих, які лежать у площині й перетинаються,
то вона перпендикулярна до даної площини
(див. рисунок).
Теорема
3. Якщо пряма перпендикулярна до двох
прямих, які лежать у площині й перетинаються,
то вона перпендикулярна до даної площини
(див. рисунок).
![]() Зверніть
увагу: якщо пряма перпендикулярна до
однієї прямої площини, то цього не досить
для перпендикулярності прямої і
площини.
На рисунку
Зверніть
увагу: якщо пряма перпендикулярна до
однієї прямої площини, то цього не досить
для перпендикулярності прямої і
площини.
На рисунку
![]() ,
але a
не перпендикулярна до
,
але a
не перпендикулярна до
![]() ,
зокрема a
не перпендикулярна до с.
,
зокрема a
не перпендикулярна до с.
![]() Теорема
4. Через точку, яка не належить даній
площині, можна провести пряму,
перпендикулярну до даної площини, і
тільки одну.
Теорема 5. Через дану
точку площини можна провести одну, й
тільки одну, перпендикулярну до неї
пряму.
Теорема 6. Через дану точку
прямої можна провести одну, й тільки
одну, перпендикулярну до неї площину.
Теорема
7. Через точку, яка не лежить на прямій,
можна провести одну, й тільки одну,
площину, перпендикулярну до даної
прямої.
Теорема 8. Якщо площина
перпендикулярна до однієї з двох
паралельних прямих, то вона перпендикулярна
й до другої.
На рисунку
Теорема
4. Через точку, яка не належить даній
площині, можна провести пряму,
перпендикулярну до даної площини, і
тільки одну.
Теорема 5. Через дану
точку площини можна провести одну, й
тільки одну, перпендикулярну до неї
пряму.
Теорема 6. Через дану точку
прямої можна провести одну, й тільки
одну, перпендикулярну до неї площину.
Теорема
7. Через точку, яка не лежить на прямій,
можна провести одну, й тільки одну,
площину, перпендикулярну до даної
прямої.
Теорема 8. Якщо площина
перпендикулярна до однієї з двох
паралельних прямих, то вона перпендикулярна
й до другої.
На рисунку
![]() ;
;
![]() ;
;
![]() .
.
![]() Теорема
9. Дві прямі, перпендикулярні до однієї
й тієї самої площини, паралельні.
Теорема
9. Дві прямі, перпендикулярні до однієї
й тієї самої площини, паралельні.
№26.Еліпс, його рівняння.
Еліпсом називається геометричне місце точок, сума відстаней яких до двох фіксованих точок, що називаються фокусами, є величина стала.
Канонічне рівняння еліпса:
![]()

A, A1, B, B1 – вершини еліпса
АА1, ВВ1 – осі еліпса
F1, F2 - фокуси еліпса
№27.Гіпербола, її рівняння.
Гіперболою називається множина точок площини, для яких модуль різниці відстаней від двох фіксованих точок, що називаються фокусами є величина стала і менша відстані між фокусами.
канонічне рівняння гіперболи:
![]()
![]()


Гіпербола та її фокуси Гіпербола та її напіввіссі та асимптоти.
№28.Парабола, її рівняння.
Параболою називається множина точок площини, кожна з яких знаходиться на однаковій відстані від фіксованої точки, яка називається фокусом, і від фіксованої прямої, яка називається директрисою і не проходить через фокус.
y2 = 2px – рівняння параболи.

Властивості
Парабола - крива другого порядку.
Вона має вісь симетрії, що називається віссю параболи. Вісь проходить через фокус і перпендикулярна директрисі.
Оптична властивість. Пучок променів, паралельних осі параболи, відбиваючись у параболі, збирається в її фокусі. І навпаки, світло від джерела, що знаходиться у фокусі, відображається параболою в пучок паралельних її осі променів.
Якщо фокус параболи відобразити щодо дотичній, то його образ буде лежати на директрисі.
Парабола є антиподерою прямій.
Всі параболи подібні. Відстань між фокусом і директрисою визначає масштаб.
При обертанні параболи навколо осі симетрії виходить еліптичний параболоїд.
Еволютою параболи є напівкубічна парабола.
