
- •Розділ 3. Лінійні системи диференціальних рівнянь
- •3.2. Лінійні неоднорідні системи.
- •3.3. Лінійні системи зі сталими коефіцієнтами.
- •Розділ 4. Нормальні системи диференціальних рівнянь
- •4.2. Перші інтеграли нормальної системи .
- •4.4. Симетрична форма системи диференціальних рівнянь.
- •Розділ 5. Рівняння з частинними похідними першого порядку
- •5.1. Постановка задачі про інтегрування рівнянь з частинними похідними.
- •5.2. Лінійне однорідне рівняння з частинними похідними першого порядку.
- •5.3. Задача Коші для лінійного однорідного рівняння в частинних похідних першого порядку.
- •5.4. Квазілінійне рівняння з частинними похідними першого порядку.
- •5.5. Задача Коші для квазілінійного рівняння.
Розділ 3. Лінійні системи диференціальних рівнянь
3.1. Загальна теорія лінійних однорідних систем. У цьому розділі ми розглянемо один клас нормальних систем диференціальних рівнянь – системи лінійних диференціальних рівнянь. Це системи вигляду
 (3.1.1)
(3.1.1)
Стосовно коефіцієнтів
![]() і функцій
і функцій
![]() припускаємо, що вони неперервні у
проміжку
припускаємо, що вони неперервні у
проміжку
![]() .
Тоді згідно з теоремою Коші для нормальних
систем існує єдиний розв’язок системи
(3.1.1) у проміжку
,
який задовольняє початкові умови
.
Тоді згідно з теоремою Коші для нормальних
систем існує єдиний розв’язок системи
(3.1.1) у проміжку
,
який задовольняє початкові умови
![]() .
(3.1.2)
.
(3.1.2)
Введемо позначення
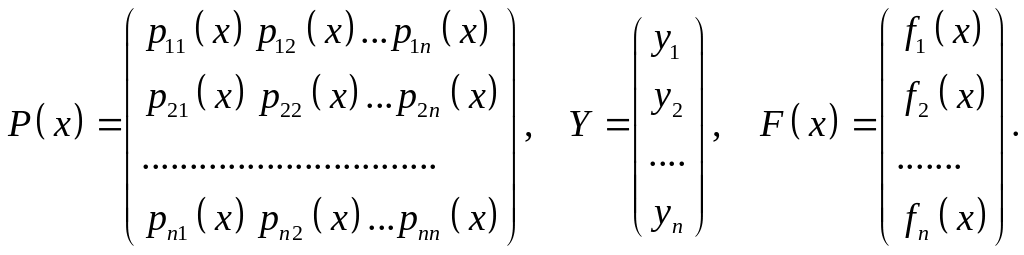
Тоді систему (3.1.1) можна записати у вигляді
![]() .
(3.1.3)
.
(3.1.3)
Якщо
![]() ,
то систему називають лінійною однорідною,
якщо хоча би одна з функцій
відмінна від нуля, то систему називають
неоднорідною.
,
то систему називають лінійною однорідною,
якщо хоча би одна з функцій
відмінна від нуля, то систему називають
неоднорідною.
Розглянемо спочатку лінійну однорідну систему
![]() .
(3.1.4)
.
(3.1.4)
Вектор-функцію
 називають розв’язком системи (3.1.4), якщо
вона перетворює рівняння системи в
тотожності, тобто
називають розв’язком системи (3.1.4), якщо
вона перетворює рівняння системи в
тотожності, тобто
![]() .
.
Теорема 3.1.
Якщо
![]() і
і
![]() – частинні розв’язки лінійної однорідної
системи, то їх сума
– частинні розв’язки лінійної однорідної
системи, то їх сума
![]() також буде розв’язком цієї системи.
також буде розв’язком цієї системи.
Згідно умови
теореми
![]()
![]() .
Використовуючи властивість лінійного
оператора, одержуємо
.
Використовуючи властивість лінійного
оператора, одержуємо
![]() .
.
Теорема доведена.
Теорема 3.2.
Якщо
![]() частинний розв’язок лінійної однорідної
системи, то
частинний розв’язок лінійної однорідної
системи, то
![]() також буде розв’язком цієї системи за
будь-якої сталої
також буде розв’язком цієї системи за
будь-якої сталої
![]() .
.
Доводиться аналогічно.
Наслідок. Якщо
![]() частинні розв’язки лінійної однорідної
системи, то розв’язком цієї системи
буде функція
частинні розв’язки лінійної однорідної
системи, то розв’язком цієї системи
буде функція
![]() .
(3.1.5)
.
(3.1.5)
Означення.
Вектор-функції
![]() називають лінійно залежними на проміжку
,
якщо існують такі числа
називають лінійно залежними на проміжку
,
якщо існують такі числа
![]() ,
не всі одночасно рівні нулю, що для усіх
,
не всі одночасно рівні нулю, що для усіх
![]() виконується тотожність
виконується тотожність
![]() .
(3.1.6)
.
(3.1.6)
Якщо ж ця тотожність
можлива лише тоді, коли усі
![]() ,
то вектор-функції називають лінійно
незалежними.
,
то вектор-функції називають лінійно
незалежними.
Розглянемо систему вектор-функцій

Утворимо визначник, який називають визначником Вронського
 .
.
Теорема 3.3.
Якщо система вектор-функцій
лінійно залежна у проміжку
,
то
![]() у проміжку
.
у проміжку
.
Згідно умови теореми виконується тотожність (3.1.6). Запишемо цю рівність як лінійну алгебричну систему
 (3.1.7)
(3.1.7)
Розглядаючи систему (3.1.7) як лінійну однорідну алгебричну систему стосовно чисел , ми бачимо , що вона має ненульовий розв’язок. Це означає, що визначник системи тотожньо дорівнює нулю. Але цей визначник і є визначником Вронського. Теорема доведена.
Теорема 3.4. Якщо лінійно незалежні у проміжку частинні розв’язки лінійної однорідної системи, то їх визначник Веронського не обертається в нуль ні в одній точці проміжку .
Допустимо протилежне.
Нехай
![]() .
Введемо позначення
.
Введемо позначення
![]() .
Утворимо систему
.
Утворимо систему
 (3.1.8)
(3.1.8)
Система (3.1.8) є
лінійною однорідною системою стосовно
![]() .
Оскільки визначник системи є визначником
Веронського у точці
.
Оскільки визначник системи є визначником
Веронського у точці
![]() ,
а він згідно припущення дорівнює нулю,
то система (3.1.8) має ненульовий розв’язок.
Позначимо його
,
а він згідно припущення дорівнює нулю,
то система (3.1.8) має ненульовий розв’язок.
Позначимо його
![]()
![]() .
Побудуємо функцію
.
Побудуємо функцію
![]() .
.
Згідно з наслідком
з теорем 3.1 і 3.2 ця функція буде
розв’язком лінійної однорідної системи.
Оскільки
задовольняють систему (3.1.8), то
![]() .
Це означає, що
.
Це означає, що
![]() .
.
Згідно теореми
Коші розв’язок лінійної однорідної
системи з нульовими початковими умовами
![]() ,
і цей розв’язок єдиний. Тому маємо
тотожність
,
і цей розв’язок єдиний. Тому маємо
тотожність
![]() .
.
Виходить, що розв’язки лінійно залежні, що суперечить умові теореми.
З двох останніх теорем можемо зробити такий висновок:
Визначник Вронського
![]() розв’язків лінійної однорідної системи
або тотожньо дорівнює нулю у проміжку
неперервності коефіцієнтів, або не
обертається в нуль ні в одній точці
цього проміжку.
розв’язків лінійної однорідної системи
або тотожньо дорівнює нулю у проміжку
неперервності коефіцієнтів, або не
обертається в нуль ні в одній точці
цього проміжку.
Означення. Систему лінійно незалежних частинних розв’язків лінійної однорідної системи називають фундаментальною системою.
Теорема 3.5. Якщо коефіцієнти лінійної однорідної системи неперервні у проміжку , то існує фундаментальна система розв’язків, визначених і неперервних у цьому проміжку.
Візьмемо довільний визначник, який відмінний від нуля.
 .
.
Визначимо частинних розв’язків системи, які задовольняють початкові умови
![]() .
.
Згідно теореми
Коші ці розв’язки існують. Визначник
Вронського цієї системи у точці
![]() співпадає з визначником
співпадає з визначником
![]() ,
тому відмінний від нуля. Отже, ця система
розв’язків є фундаментальною.
,
тому відмінний від нуля. Отже, ця система
розв’язків є фундаментальною.
Теорема 3.6. Якщо фундаментальна система розв’язків лінійної однорідної системи у проміжку , то формула
(3.1.9)
дає загальний розв’язок цієї системи у проміжку .
Ми вже знаємо, що функція (3.1.9) є розв’язком лінійної однорідної системи. Треба довести, що з цієї формули можна одержати будь-який частинний розв’язок. Виберемо довільний частинний розв’язок, задавши довільні початкові умови.
![]() ,
(3.1.10)
,
(3.1.10)
де
![]() довільно задані числа. Згідно з теоремою
Коші задача (3.1.4) – (3.1.10) має єдиний
розв’язок. Треба показати, що він
міститься у формулі (3.1.9). Підставимо
початкові умови (3.1.10) у формулу (3.1.9).
Одержимо систему
довільно задані числа. Згідно з теоремою
Коші задача (3.1.4) – (3.1.10) має єдиний
розв’язок. Треба показати, що він
міститься у формулі (3.1.9). Підставимо
початкові умови (3.1.10) у формулу (3.1.9).
Одержимо систему
 (3.1.11)
(3.1.11)
Система (3.1.11) –
лінійна неоднорідна система, визначник
якої є визначником Вронського
![]() фундаментальної системи розв’язків.
Тому цей визначник відмінний від нуля.
Отже, система (3.1.11) має єдиний розв’язок.
Позначимо його
фундаментальної системи розв’язків.
Тому цей визначник відмінний від нуля.
Отже, система (3.1.11) має єдиний розв’язок.
Позначимо його
![]() .
Підставимо ці числа у формулу (3.1.9).
.
Підставимо ці числа у формулу (3.1.9).
.
Це й буде шуканий розв’язок. Теорема доведена.
Теорема 3.7.
Будь-які
![]() частинні розв’язки лінійної однорідної
системи
рівнянь будуть лінійно залежними.
частинні розв’язки лінійної однорідної
системи
рівнянь будуть лінійно залежними.
Доведення аналогічне
доведенню відповідної теореми для
лінійного однорідного рівняння
![]() го
порядку.
го
порядку.
Формула Остроградського-Ліувілля.
Обчислимо похідну визначника Вронського фундаментальної системи
![]() .
.
![]() визначник,
отриманий з
визначник,
отриманий з
![]() шляхом диференціювання
шляхом диференціювання
![]() го
рядка. Розглянемо
го
рядка. Розглянемо
![]() і врахуємо той факт, що
частинні розв’язки лінійної однорідної
системи (3.1.4).
і врахуємо той факт, що
частинні розв’язки лінійної однорідної
системи (3.1.4).

 ,
,
бо в останньому визначнику
перший рядок є лінійною комбінацією
решти
![]() го
рядків, тому він дорівнює нулю. Аналогічно
отримуємо, що
го
рядків, тому він дорівнює нулю. Аналогічно
отримуємо, що
![]() .
Тоді
.
Тоді
![]() .
.
Інтегруємо це диференціальне рівняння
![]() .
.
Підставивши у цю формулу
,
одержуємо
![]() .
Остаточно
.
Остаточно
![]() .
.
Останню формулу і називають формулою Остроградського- Ліувілля для лінійних систем.
