Найпростіші властивості еліпса
Властивість 1. Еліпс має що найменше дві осі симетрії і центр симетрії.
□ Дійсно,
якщо точка 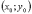 належить
еліпсу в канонічній системі координат,
тобто
належить
еліпсу в канонічній системі координат,
тобто 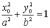 ,
то і точки
,
то і точки  ,
, 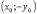 і
і 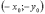 належать
еліпсу. А це означає, що осі координат
канонічної системи координат є осями
симетрії еліпса, а її початок координат
– центром симетрії. ■
належать
еліпсу. А це означає, що осі координат
канонічної системи координат є осями
симетрії еліпса, а її початок координат
– центром симетрії. ■
Зауваження. Можна показати, що еліпс, який не є колом має рівно дві осі симетрії.
Властивість 2. Еліпс перетинає осі симетрії у чотирьох точках.
□ В
канонічній системі координат точки
перетину еліпса з осями симетрії
знаходяться з рівнянь 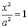 і
і 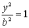 і
мають, відповідно, координати
і
мають, відповідно, координати 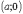 ,
, 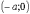 ,
,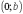 ,
, 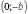 . ■
. ■
Означення. Точки перетину еліпса з осями симетрії називаються вершинами еліпса.
Властивість
3. Еліпс
є обмеженою фігурою, він міститься у
прямокутнику зі сторонами 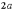 і
і 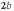 .
.
□ З
рівняння еліпса маємо: 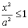 і
і 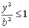 ,
або
,
або 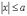 і
і 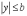 .
Останні нерівності визначають прямокутник
зі сторонами
і
. ■
.
Останні нерівності визначають прямокутник
зі сторонами
і
. ■
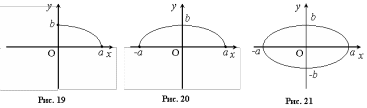
Отриманої
інформації достатньо, щоб зобразити
еліпс у канонічній системі координат,
користуючись його властивостями. У I
чверті дуга еліпса визначається
рівнянням 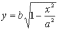 ,
тобто є графіком деякої функції (рис.
19).
,
тобто є графіком деякої функції (рис.
19).
|
|
|
|
Скористувавшись
наявністю двох осей симетрії, побудуємо
увесь еліпс (рис. 20 і рис. 21).
Параметри  і
і 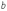 називають півосями (
‑ більшою,
‑ меншою).
Вони дорівнюють половинам відстаней
між відповідними протилежними вершинами
еліпса.
називають півосями (
‑ більшою,
‑ меншою).
Вони дорівнюють половинам відстаней
між відповідними протилежними вершинами
еліпса.
Форму
еліпса характеризує параметр 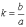 .
Він є коефіцієнтом стиснення кола, з
якого можна отримати еліпс шляхом
стиснення або розтягування. Більш
зручним у дослідженнях є параметр
.
Він є коефіцієнтом стиснення кола, з
якого можна отримати еліпс шляхом
стиснення або розтягування. Більш
зручним у дослідженнях є параметр  .
Він називається ексцентриситетом еліпса.
Ексцентриситет кола дорівнює 0.
.
Він називається ексцентриситетом еліпса.
Ексцентриситет кола дорівнює 0.
Найпростіші властивості гіперболи
Аналогічно
можна дослідити властивості гіперболи.
Нехай дано рівняння гіперболи 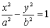 ,
,
,
, 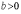 .
Відповідна система координат
називаєтьсяканонічною.
.
Відповідна система координат
називаєтьсяканонічною.
Властивість 1. Гіпербола має щонайменше дві осі симетрії і центр симетрії.
Доведення аналогічно наведеному для еліпса. Спробуйте довести, що у гіперболи рівно дві осі симетрії.
Властивість 2. Гіпербола перетинає одну з осей симетрії в двох точках, які називаються вершинами; з другою віссю симетрії гіпербола не перетинається.
□ Точки
перетину знаходяться з рівнянь
, 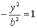 .
Тому вершинами гіперболи в канонічній
системі координат є точки
.
Тому вершинами гіперболи в канонічній
системі координат є точки 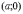 ,
, 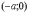 . ■
. ■
Властивість 3. Гіпербола має асимптоти, тобто прямі, до яких гіпербола необмежено наближається.
□ Розглянемо
гіперболу в канонічній системі
координат: 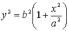 .
Тоді
.
Тоді 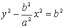 ,
а
,
а 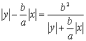 .
Якщо
.
Якщо 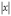 набуває
великі значення, то
набуває
великі значення, то 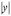 мало
відрізняється від
мало
відрізняється від 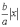 .
Тому відстань від точок гіперболи до
прямої
.
Тому відстань від точок гіперболи до
прямої 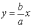 ,
або до прямої
,
або до прямої 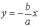 ,
прямує до нуля, якщо точки гіперболи
прямують до нескінченності. ■
,
прямує до нуля, якщо точки гіперболи
прямують до нескінченності. ■
 Побудуємо
гіперболу, скориставшись її властивостями.
У I чверті дуга гіперболи визначається
рівнянням
Побудуємо
гіперболу, скориставшись її властивостями.
У I чверті дуга гіперболи визначається
рівнянням 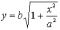 і
має вигляд, показаний на рис. 22.
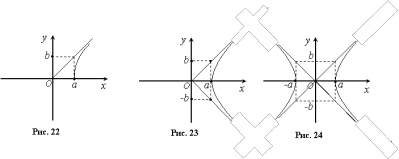
Використовуючи осі симетрії гіперболи,
отримаємо її повністю (рис. 23 і
24).
і
має вигляд, показаний на рис. 22.
Використовуючи осі симетрії гіперболи,
отримаємо її повністю (рис. 23 і
24).
Параметри
і
також
називають півосями
гіперболи,
‑ дійсною,
‑ уявною.
Параметр 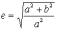 називається ексцентриситетом.
Він характеризує форму гіперболи.
називається ексцентриситетом.
Він характеризує форму гіперболи.