5.4. Полюс и поляра.

Опр. 5.4.1. Пусть кривая 2 порядка  задана в плоскости (; ¯ уравнением (5.1.1), и A(a_i ) – произвольная точка плоскости (; ¯ . Полярой точки A относительно  называется множество точек, координаты которых удовлетворяют уравнению

(;\s\do10(i(а_ij a_i) x_j = 0  (;\s\do10( j =1u_j x_j = 0 , (5.4.1)

где мы обозначили u_j = (;\s\do10(i =1а_ij a_i. Мы видим, что поляра – это прямая (если не все u_j = 0). Точка A называется полюсом этой прямой. Уравнение (5.4.1) совпадает с (5.3.2), и поэтому, если A  , то полярой к A будет касательная к кривой в точке A .

5.5. Геометрический смысл поляры.

Опр. 5.5.1. Точка B называется сопряженной с точкой A относительно кривой , если (ABM₁M₂) = –1, где {M₁, M₂} = AB  .

О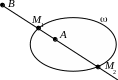 чевидно, что

1. если B сопряжена с A , то A сопряжена с B;

2. на каждой прямой, которая проходит через A , существует единственная точка B, сопряженная с A (четвертая гармоническая к M₁, M₂, A ).

Пусть заданы точки A(a_i ), B(b_i ) и кривая  с помощью уравнения (5.1.1). По определению (ABM₁M₂) = –1. Поскольку {M₁, M₂}  AB, то координаты M₁, M₂ можно записать так: ₁a_i + ₁b_i , ₂a_i + ₂b_i , где ₁/₁ и ₂/₂ – корни уравнения (5.2.2). В соответствии с (4.2.2)

(ABM₁M₂) = : .

Поэтому

: = –1  + = 0 .

По теореме Виета для уравнения (5.2.2) получаем

(;\s\do10(iа_ij a_ib_j = 0, (5.5.1)

Это и есть условие сопряженности точек относительно кривой .

Сравним теперь (5.5.1) и (5.4.1). Мы видим, что справедлива следующая теорема.

Теорема 5.5.1. Поляра точки A относительно кривой второго порядка  есть множество точек, сопряженных к A относительно .

5.6. Принцип взаимности поляр.

Теорема 5.6.1. Если точка B принадлежит поляре точки A, то A принадлежит поляре точки B.

Пусть кривая  имеет уравнение (5.1.1), а точки A и B – координаты a_i и b_i . Пусть p(A) и p(B) – поляры точек A и B. Уравнение p(A): (;\s\do10(i(а_ij a_i) x_j = 0 ; уравнение p(B): (;\s\do10(i(а_ij b_i) x_j = 0 ;

B p(A)  (;\s\do10(iа_ij a_ib_j = 0  (;\s\do10(iа_ij b_ia_j = 0  A p(B) .

И з этой теоремы вытекает удобный способ построения поляры. Необходимо рассмотреть два случая:

1) из точки A можно провести 2 касательные к кривой ;

2) из A нельзя провести ни одной касательной к .

1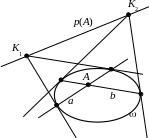 . Пусть l₁ и l₂ – касательные к , проведенные из точки A, а P и Q – точки касания. Тогда l₁= p(P), l₂= p(Q). Значит, A p(P) и A p(Q)  P p(A) и Q p(A)  PQ = p(A).

Тот же рисунок показывает, как построить полюс прямой PQ, если она пересекает .

2. Проведем через точку A две произвольные прямые a и b. Построим полюсы этих прямых: K₁ и K₂. Тогда

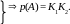A a = p(K₁)  K₁ p(A)

A b = p(K₂)  K₂ p(A)

И обратно, если дана прямая K₁K₂, мы можем построить ее полюс A.

Пример. Дано уравнение кривой : х₁² – х₂² + 2х₃² + 4х₁х₂ – 2х₂х₃ = 0 и точка B(0: 2: –1)  .

Уравнение поляры запишем в матричном виде: B^TAX = 0, или

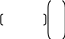1 2 0 х₁ х₁

0 2 –1 2 –1 –1 х_{2 = 0}; _{ 4 –1 –4} х_{2 = 0}; _

0 –1 2 х₃ х₃

4х₁ – х₂ – 4х₃ = 0 _.