2.10. Статистическая модель разрушения км.

Виды разрушения КМ. Выше рассмотрена прочность КМ в предположении, что у всех волокон предел прочности одинаков и разрушаются они одновременно- при достижении определенного уровня напряжений. На практике в свойствах волокон всегда есть разброс. Если композиция состоит из прочных, пластичных волокон и пластичной матрицы, то разброс прочностных характеристик компонентов мал и прочность такого КМ без большой погрешности можно выразить уравнением аддитивности. Разрушаются такие КМ из-за неустойчивости пластического течения с образованием шейки и одновременным разрывом всех волокон.

Если же композиция состоит из хрупких волокон с большим разбросом прочности и малопластичной матрицы (например, боропластики, углепластики, стеклопластики), то использование при оценке прочности КМ средней прочности волокон приводит к большим погрешностям. Для таких КМ нужен статистический подход к оценке прочности.

При нагружении КМ хрупкая матрица- хрупкое волокно разрыв, появившийся в одном сечении, не приводит к разрушению всех волокон в том де сечении, поскольку внутренние дефекты в волокнах распределены статистически по всей их длине. За первым разрывом в одном сечении следует разрыв другого волокна в другом сечении. Эти разрывы накапливаются по длине образца и по достижении некоторого критического состояния приводят к разрушению КМ в целом. Такой вид разрушения и положен Б. Розеном в основу статистической теории прочности КМ.

В соответствии со статистической теорией прочности КМ следует рассматривать как цепь, состоящую из последовательно соединенных звеньев небольшой длины. Разрушается КМ при разрыве одного из этих звеньев. Б. Розен предлагает принять длину звеньев равной неэффективной длине l* волокон, поскольку на этой длине концы разрушенных волокон не создают упрочнения, а выполняют роль дефектов, определяющих прочность звена композиции. Оставшиеся неразрушенными волокна принимают на себя всю нагрузку. Каждое звено рассматривается как пучок волокон, и прочность КМ рассчитывается как прочность пучка волокон длиной l*. Таким образом, задача сводится к установлению зависимости прочности пучка волокон от их длины и разброса свойств. Но прежде чем перейти к ее решению, напомним основные понятия из теории вероятностей, которые нам понадобятся.

Некоторые положения теории вероятностей. Вероятностью Р(А) события А называют отношение случаев , в которых это событие осуществляется, к общему числу всех операций:

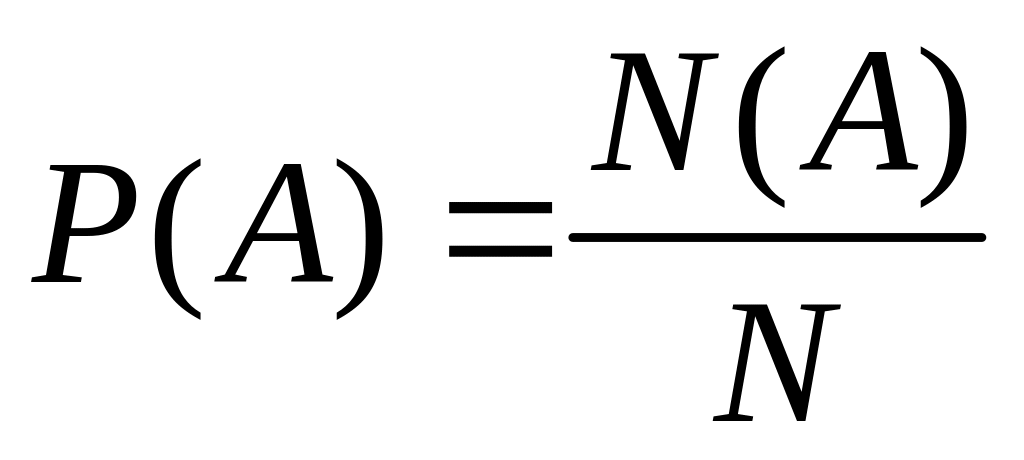, (1.81)

где N- общее число операций;

N(A)- число тех операций, в которых событие А осуществляется.

Правило сложения вероятностей гласит, что вероятность наступления в некоторой операции какого-либо (безразлично, какого именно) из результатов равна сумме вероятностей этих результатов, если каждые два из них несовместимы между собой. Несовместимыми называют такие результаты, которые в одной и той же единичной операции наблюдаться не могут. Правило сложения вероятностей можно записать в виде

Р( или , или , или …)= Р( )+Р( )+Р( )+… (1.82)

Если вероятность Р( ), Р( ), Р( ),… наступления n событий одинакова, то

Р( или , или , или …)= nР , (1.83)

где Р -вероятность каждого их этих событий.

Если из двух событий и наступить в некоторой операции может только одно, то такие события называются противоположными. Очевидно, что сумма вероятностей двух противоположных событий

Р( )+Р( )=1.

Пусть имеется n событий таких, что в каждой единичной операции обязательно должно наступить одно и только одно из этих событий. Такая группа событий называется полной системой. Сумма вероятностей этих событий

Р( )+Р( )+Р( )+…+Р =1. (1.84)

Если вероятность события В не зависит от того, произошло или нет событие А, то события А и В называются взаимно независимыми.

Правило умножения вероятностей: вероятность совместного наступления любого числа взаимно независимых событий равна произведению вероятностей этих событии:

Р(А и В, и С, и …)=Р(А) Р(В) Р(С)… (1.85)

Если Р(А)=Р(В)=Р(С)=… , то Р(А и В, и С, и …)= . (1.86)

Функция, показывающая, с какой вероятностью случайная величина принимает то или иное числовое значение, называется функцией распределения вероятностей. Для непрерывной случайной величины она представляет собой функцию, называемую плотностью вероятности (рис. 16, а). В этом случае величина р(х)dх выражает вероятность того, что случайная величина примет значение, лежащее между х и х+ dх. Функцию р(х) называют также интегральная функция распределения. Исчерпывающей количественной характеристикой случайной величины может быть также интегральная функция распределения Р(х) (рис. 16, б), которая характеризует вероятность того, что случайная величина х примет значение, меньшее заданного Х. между дифференциальной и интегральной функциями распределения существуют такие зависимости:

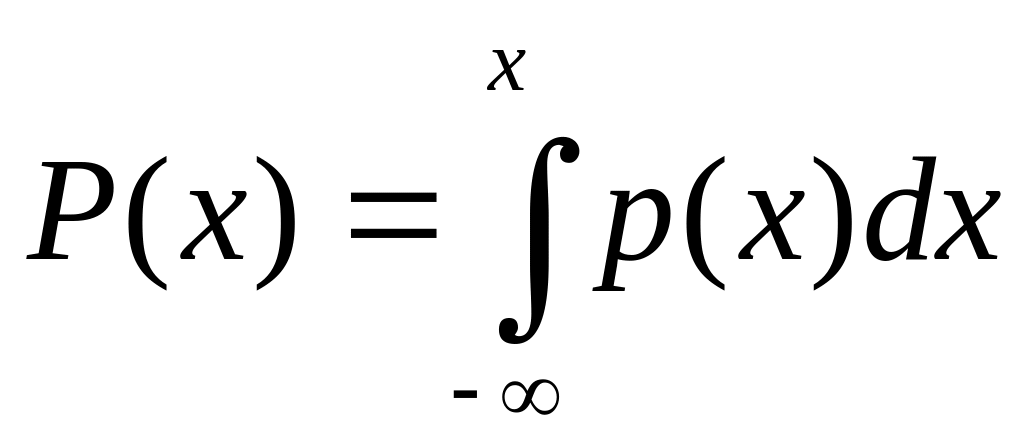, (1.87)

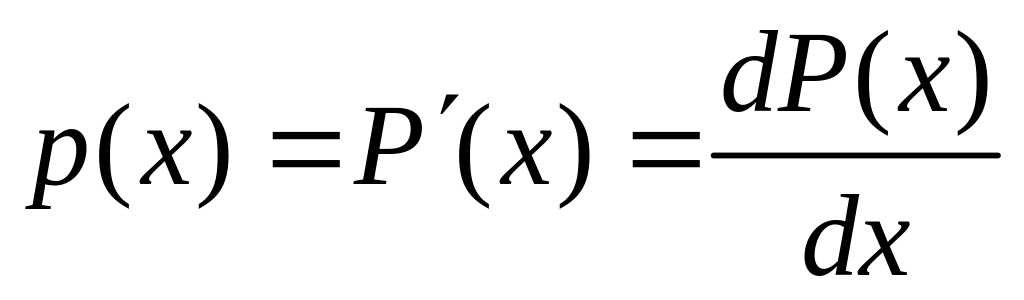. (1.88)

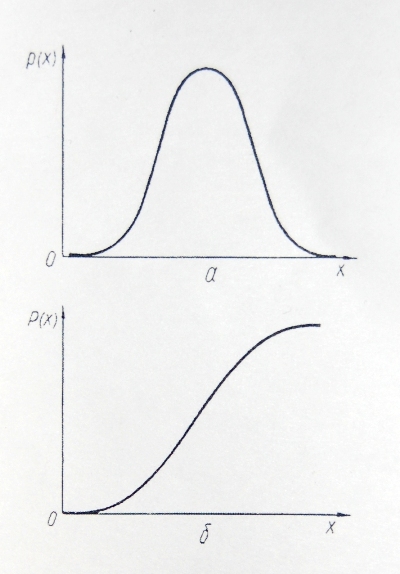
Рис.16. Дифференциальная (а) и интегральная (б) функция распределения непрерывной случайной величины.

Перейдем теперь к анализу прочности пучка волокон.

Прочность пучка волокон.

Рассмотрим вначале, как зависит вероятность разрушения одного волокна от его длины.

Волокно длиной l мысленно разделим на равные отрезки, длина которых равна диаметру волокна. Число таких отрезков

. (1.89)

Всегда имеющиеся в волокне дефекты (они могут появиться или при нагружении волокон) статистически распределены по всей длине. Наличие их определяет прочность каждого отрезка.

Совокупность прочностей отрезков можно охарактеризовать функцией распределения f(σ), где f(σ)dσ – вероятность того, что данный отрезок разрушится в интервале напряжений σ… σ+ dσ.

Вероятность того, что все ω отрезков разрушатся при напряжении, меньшем определенного уровня σ , выразится интегральной функцией распределения прочности

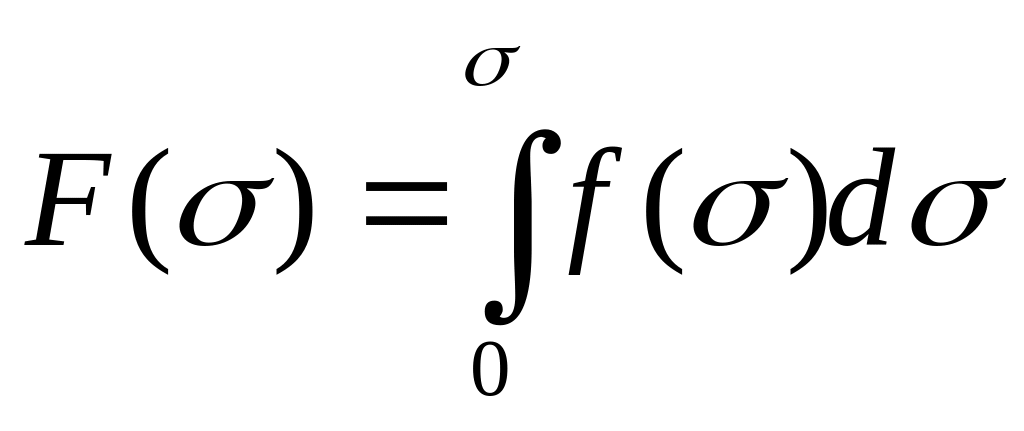. (1.90)

Ясно, что при напряжении, меньшем σ, вероятность неразрушения любого отрезка составит [1-F(σ)], ибо разрушение и неразрушение волокна- события противоположные.

Представим теперь, что все волокно ведет себя как цепь из ω звеньев. Разрушится оно, когда разрушится слабейшее звено этой цепи. Вероятность этого разрушения в интервале растягивающих напряжений σ… σ+ dσ характеризуется дифференциальной функцией распределения прочности волокна g(σ).

Если известно, что при напряжениях меньших или равных σ, вероятность неразрушения одного звена составляет [1-F(σ)], то вероятность неразрушения в этом интервале остальных (ω-1) звеньев по правилу (1.86) умножения вероятностей будет равна . При этом предполагается, что разрушения каждого звена не зависит от разрушения остальных звеньев.

Вероятность разрушения только в одном выбранном звене в интервале напряжений σ… σ+ dσ выразится произведением f(σ) , а сумма этих вероятностей по всем ω звеньям в соответствии с уравнением (1.83) составит f(σ) ω и определит вероятность разрушения в любом из звеньев.

Поскольку волокно разрушается при разрыве одного любого звена, сумма эта равна вероятности g(σ) разрушения и всего волокна в диапазоне напряжений σ… σ+ dσ :

g(σ)= f(σ) ω. (1.91)

вероятность разрушения волокна в интервале 0… σ определяется интегральной функцией G(σ) распределения прочности волокон:

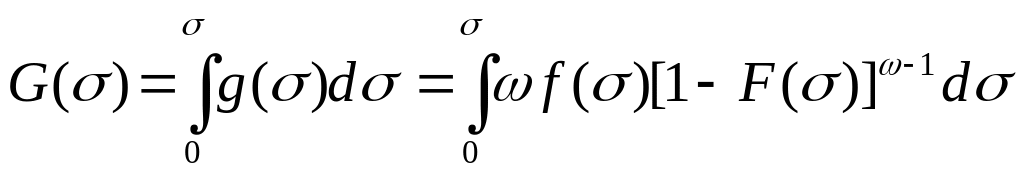. (1.92)

(стр.54 капр)

Проинтегрировав уравнение (1.92), получим:

(1.93)

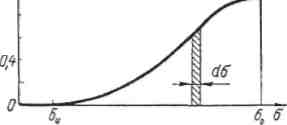
Рис.17. Функция G( ) распределения прочности стекловолокон

Выражение (1.93) позво­ляет по известной интегральной функции F( ) распределения прочности звена определить интегральную функцию G ( ) распределения прочности волокна.

На основе анализа многочисленных эксперименталь­ных данных по прочности материалов Вейбулл предло­жил задавать функцию F ( ) выражением

F ( )=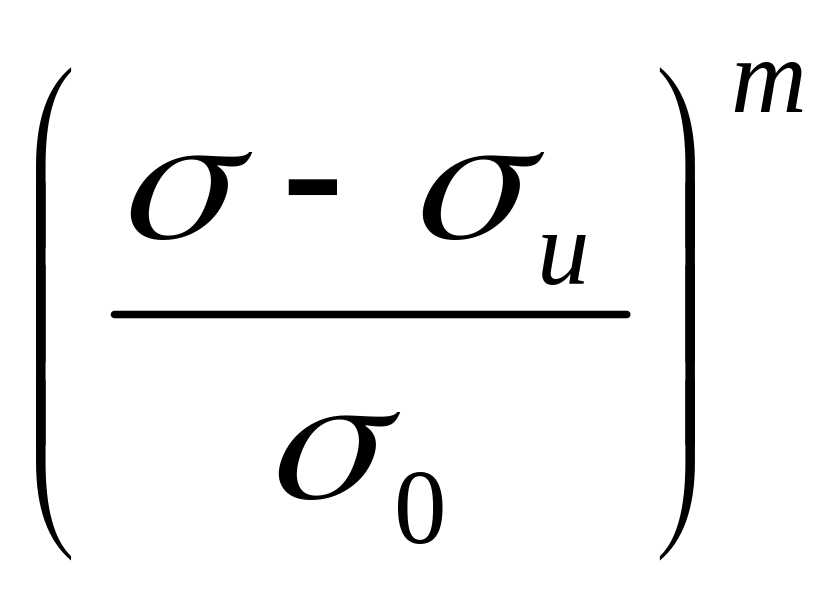 (1.94)

Где - приложение напряжение, величина которого находится в интервале между нижним и верхним пределами прочности (рис. 17). Часто в качестве нижнего предела принимают = 0. Тогда становится равным теоретиче­ской прочности материала;

т— параметр, характеризующий разброс данных. Например, коэффициент вариации прочности с, выпол­няющий роль меры относительного разброса прочности, является функцией только параметра т:

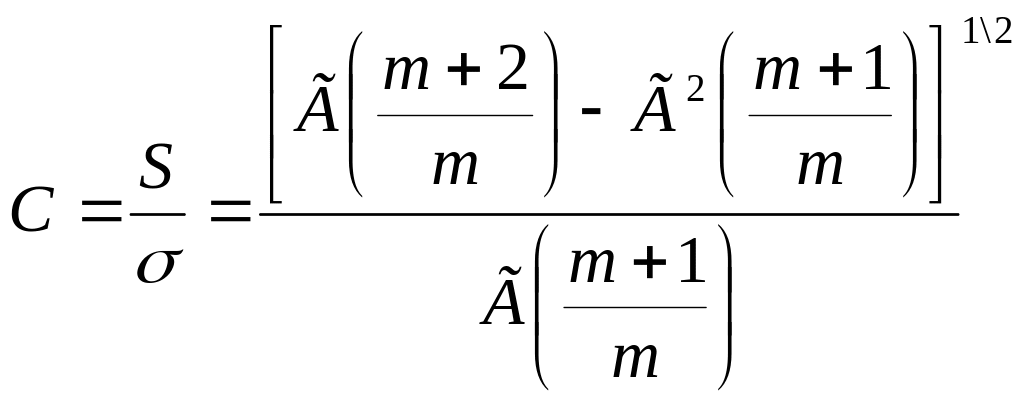(1.95)

Где Г - табулированная гамма-функция;

S - дисперсия прочности, равная квадрату стан­дартного отклонения прочности;

- средняя прочность испытанной партии мате­риалов.

По экспериментальным данным

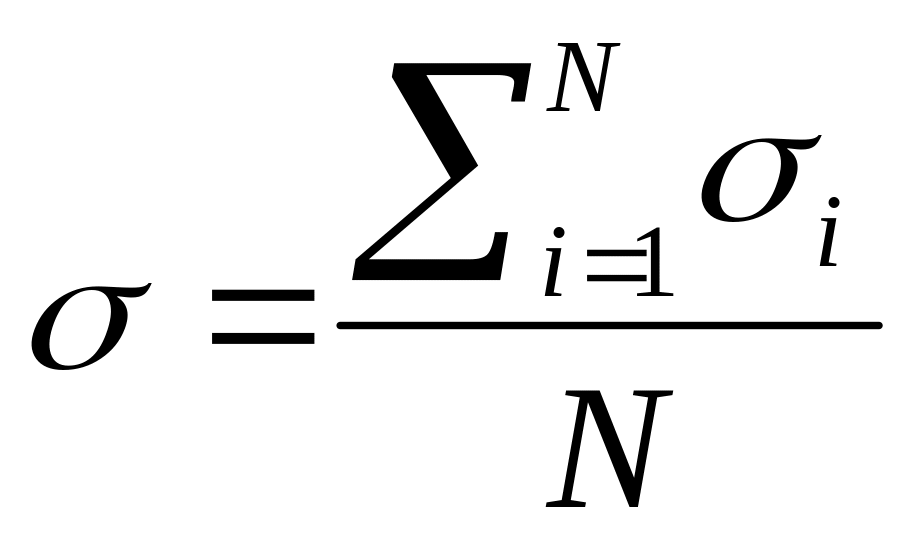; S²=

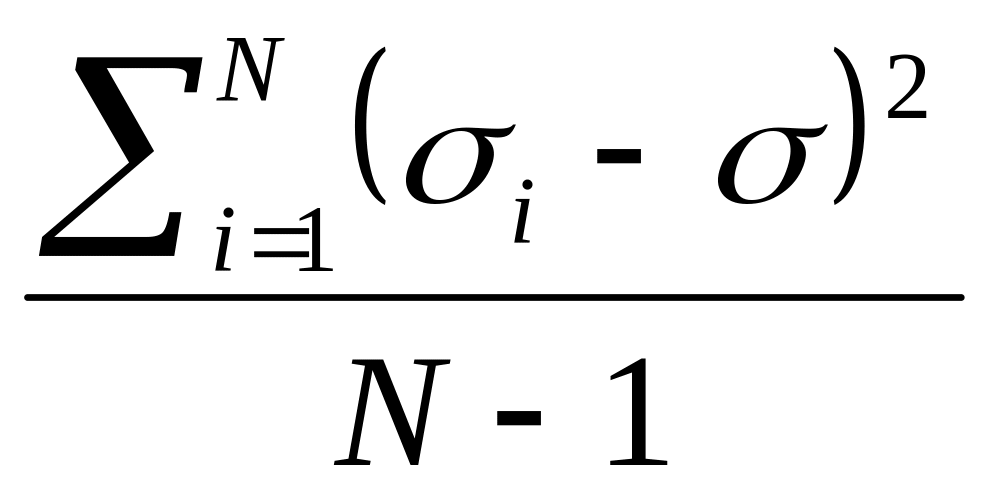
Где - прочность i-ого образца;

N - число испытанных образцов.

Приближенно зависимость (1.95) можно аппроксими­ровать более простым выражением:

(1.96)

Чем больше т, тем меньше разброс прочности мате­риала. При т разброса нет.

Подставив выражение (1.94) в уравнение (1.93), получаем

G( )= 1-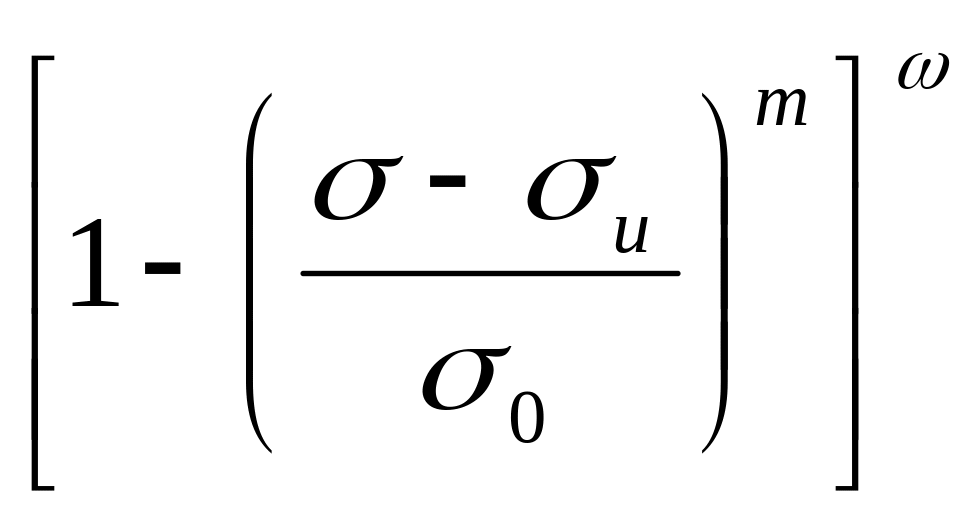 (1.97)

Для малых значений х = ( — )/ можно воспользо­ваться приближением Пуассона

1-(1-Х^m) ехр (- Х^m) (1.98)

и, используя зависимость (1.89), привести выражение (1.97) к более удобному для вычислений виду:

G( )=1-ехр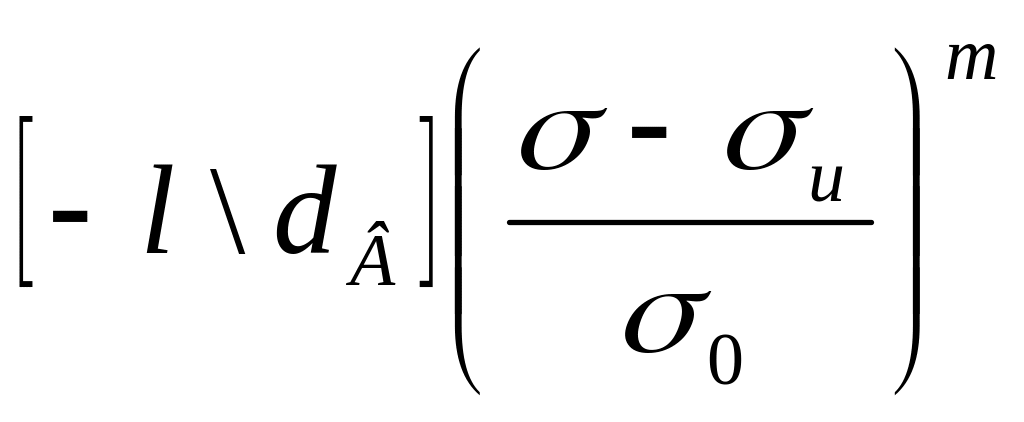 (1.99)

Таким образом, вероятность разрушения волокна при заданном напряжении возрастает по мере увели­чения отношения l/d_B. Параметры и т уравнения Вейбулла рассчитывают по результатам механических испытаний партии волокон.

Рассмотрим теперь прочность пучка волокон дли­ной I. Будем считать, что все волокна в пучке парал­лельны, не касаются друг друга и нагружаются одина­ково.

Если общая нагрузка, приложенная к пучку, равна Р_В и при этом п волокон уже разрушились, a (N — п) волокон остались целыми, то напряжение в уцелевших волокнах находят по формуле

=Р_В/А_N-n (1.100)

Где А_N-n - суммарная площадь сечений неразрушив­шихся волокон.

Отношение площади A _N-n к исходной суммарной площади всех волокон A_N определяется соотношением

(1.101)

Подставив выражение (1.101) в формулу (1.100), получим

Р_В= _ВА_N-n= (1.102)

Если из всех N испытанных волокон п волокон разрушились при напряжениях, меньших , то

(1.103)

Подставив выражение (1.103) в уравнение (1.102), с учетом выражения (1.99) получим

Р_В=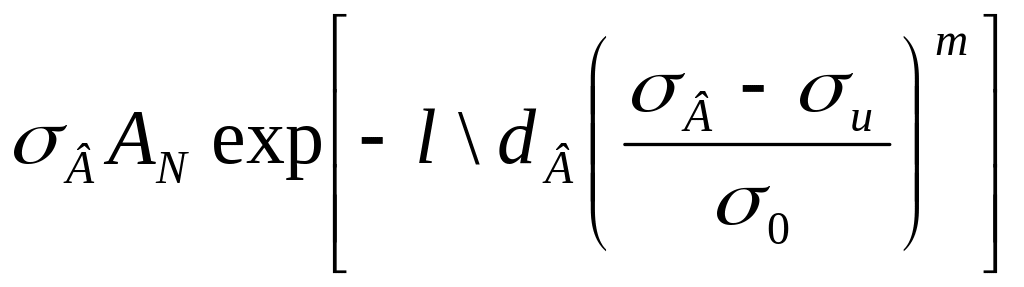 (1.104)

Нагрузка на пучок волокон достигает максимума при dPВ/d _В = 0. Примем для упрощения = 0. Про­дифференцировав зависимость (1.104) по d и решив полученное уравнение относительно , найдем макси­мальное напряжение в волокнах:

(1.105)

Подставив выражение (1.105) в уравнение (1.104), опре­делим величину максимальной нагрузки, приходящейся на пучок:

Р_Вmax = (1.106)

где е — основание натуральных логарифмов.

Прочность пучка волокон равна отношению максимальной нагрузки к площади поперечного сечения A_N всех исходных волокон:

(1.107)

Уравнение (1.107) устанавливает зависимость прочности пучка от отношения длины волокон к диаметру и пара­метра т, характеризующего разброс данных. Чем больше l/d_В. тем меньше прочность пучка волокон.

Обычно несущая способность пучка характеризуется отношением прочности пучка средней прочности отдельно испытанных волокон. Величину можно рассчитать по известным значениям параметров и m Вейбулла в соответствии с формулой

где Г—гамма-функция.

Разделив выражение (1.107) на зависимость (1.108), получим

(1/109)

Таким образом, с увеличением т, т. е. с уменьшением разброса, отношение растет. Иными словами, прочность пучка снижается быстрее, чем средняя проч­ность партии отдельно испытанных волокон. Обычно значения т =2 5 соответствуют хрупким материалам, а т 15 20 — пластичным.

На практике отношение прочности пучка к средней прочности одного волокна оказывается ниже, чем рас­считанное по уравнению (1.109). Это связано с невозмож­ностью равномерно нагрузить все волокна и обеспечить их полную параллельность.

Статистическая прочность КМ. Как уже указыва­лось (§ 8), прочность КМ в соответствии с тео­рией Б. Розена можно вычислить как прочность пучка волокон длиной, равной неэффективной длине /* волокна. Для этого в уравнение (1.107) вместо l/d_В, подставим значение l*\d_В, взятое из уравнения (1.80), и умножим _пуч на объемную долю волокон V_b. При этом пренебрежем вкладом матрицы, который во многих случаях для рас­сматриваемого класса КМ невелик. Тогда получим

=V_В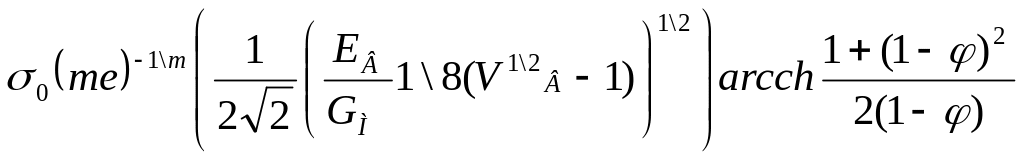 (1.110)

Уравнение (1.110) позволяет установить влияние свойств компонентов на прочность КМ. С увеличением l*id_B прочность КМ уменьшается. Анализ уравнения (1.80) показывает, что величина l*ld_B растет с увеличе­нием E_В\G_М. Использование матриц с высоким пределом текучести снижает степень пластической деформации матрицы и тем самым спо­собствует уменьшению l*/d_a, а, значит, повыше­нию ( _в)к (в § 8 уже гово­рилось о том, что чем плас­тичнее матрица, тем боль­ше 1*/ d_В. С другой стороны, применение пластич­ных матриц может изме­нить механизм разрушения КМ: пластичная матрица будет оказывать большее сопротивление распростра­нению трещин и тем са­мым способствовать повы­шению прочности компо­зиции в целом.

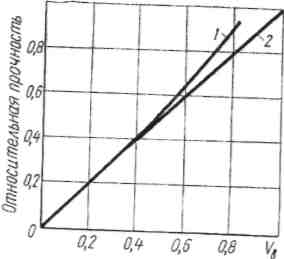
Рис. 18. Зависимость относи­тельной прочности композиции при растяжении от объемной доли волокон V' для статисти­ческой модели разрушения (l) и для правила смесей (2)

Интересно сопоставить влияние объемной концен­трации V_B волокон на прочность КМ, предсказываемое статистической теорией и правилом аддитивности. На рис. 18 кривая 1 соответствует расчету статистической теории при т — 7,7; прямая 2 — по уравнению адди­тивности в предположении, что прочность матрицы равна нулю. Для диапазона V_B = 0 0,5 линии 1 и 2 практически совпадают, при V_В > 0,5 статистическая теория предсказывает большую прочность, чем уравне­ние аддитивности.

Концентрации волокон V_К > 0,5 используются в по­лимерных КМ. Имеющиеся данные по прочности стекло­пластиков подтверждают справедливость статистической теории. В КМ на основе металлов и керамики обычно V_В < 0,5 и результаты некоторых испытаний одинаково хорошо объясняются как правилом смесей, так и статис­тической теорией. Часть из проведенных эксперимен­тальных исследований не позволяет однозначно определить, какая теория более пригодна для описания поведения КМ при растяжении, поскольку реальная прочность оказывается ниже предсказываемой обеими теориями. Это вызвано, по всей видимости, несовер­шенством технологии получения КМ.