
- •Составители: доц. Валерий Леонидович Шур
- •§1. Числовые ряды
- •§2. Признаки сходимости числовых рядов
- •§3. Знакопеременные ряды
- •§4. Степенные ряды
- •§5. Применение степенных рядов к вычислению определенных интегралов и к решению дифференциальных уравнений
- •§6. Ряды Фурье
- •Индивидуальные домашние задания
- •Библиографический список
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Самарская государственная академия путей сообщения
Кафедра «Высшая математика»
РЯДЫ
Методические указания
и индивидуальные домашние задания
для студентов 2 курса очной формы обучения
всех специальностей
Составители: Шур В.Л.
Сеницкий А.Ю.
Додонова Н.Л.
Латыпова Н.М.
САМАРА 2005
УДК 517
Ряды: Методические указания и индивидуальные домашние задания для студентов- очной формы обучения всех специальностей. – Самара.- СамГАПС, 2005. – 26 с.
Утверждено на заседании кафедры «Высшая математика» от 24.03.05 г., протокол №6.
Печатается по решению редакционно-издательского совета академии.
Методические указания и индивидуальные домашние задания составлены в соответствии с Государственным образовательным стандартом и типовой программой по высшей математике и охватывают раздел общего курса: ряды и их применение.
Указания предназначены для студентов-очников всех специальностей.
Составители: доц. Валерий Леонидович Шур
доц. Александр Юрьевич Сеницкий
доц. Наталья Леонидовна Додонова
доц. Наиля Масхутовна Латыпова
Рецензенты: к.ф.-м.н., доцент СГУ Г.В. Воскресенская
к.ф.-м.н., доцент СамГАПС В.П. Кузнецов
Под редакцией авторов
Подписано в печать 11.05.05. Формат 60 х 90 /16.
Бумага писчая. Печать оперативная. Усл. п.л. 1,6.
Тираж 100 экз. Заказ № 72.
© Самарская государственная академия путей сообщения, 2005
§1. Числовые ряды
Основные
определения. Пусть
дана бесконечная числовая последовательность
![]() .
Числовым
рядом с общим
членом
.
Числовым
рядом с общим
членом
![]() называется выражение вида
называется выражение вида
![]() .
.
Числовой ряд
обозначается
![]() .
.
Например, если
![]() ,
то ряд имеет вид:
,
то ряд имеет вид:
![]()
или
![]() .
.
Сумма первых n
членов ряда называется n-ой
частичной суммой
и обозначается
![]() ,
,
![]() .
Так, например,
.
Так, например,
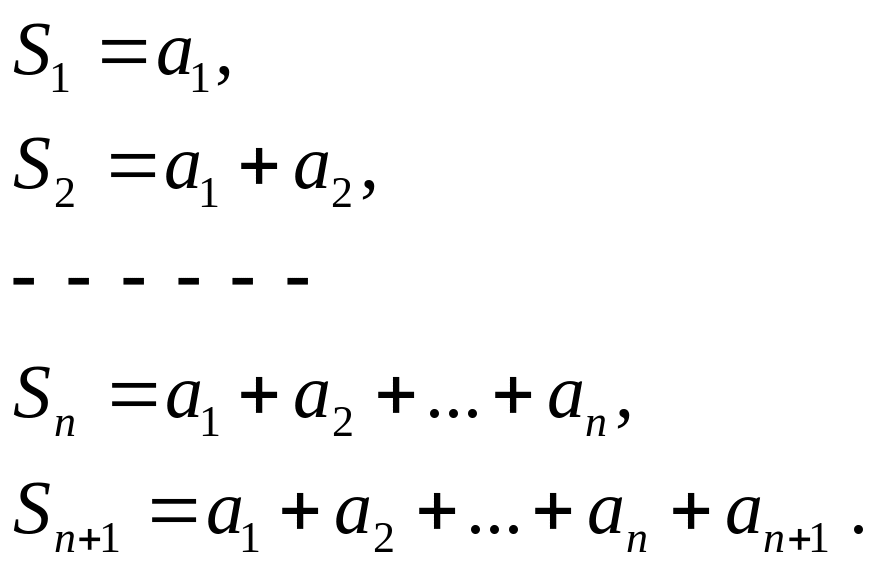
Последовательность
![]() называется последовательность
n-ых
частичных сумм.
называется последовательность
n-ых
частичных сумм.
Числовой ряд
называется сходящимся,
если последовательность его частичных
сумм имеет конечный предел, то есть если
существует предел
![]() .
Значение s
этого предела называется суммой
ряда
.
Если последовательность частичных сумм
не имеет конечного предела, ряд называется
расходящимся.
.
Значение s
этого предела называется суммой
ряда
.
Если последовательность частичных сумм
не имеет конечного предела, ряд называется
расходящимся.
Пример 1.1. Исследовать на сходимость ряд
![]()
Решение.
Пользуясь известным тождеством
![]() ,
находим, что
,
находим, что
![]() .
.
Так как
![]() ,
,
то ряд сходится и его сумма равна 1.
Пример 1.2. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии
![]() ,
где
,
где
![]() .
.
Решение.
Известно, что сумма n
первых членов
геометрической прогрессии вычисляется
по формуле
![]() .
.
Тогда
![]() .
.
Если
![]() ,
то
,
то
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
.
Таким образом, ряд
![]() ,
составленный из членов геометрической
прогрессии сходится при
и расходится при
.
,
составленный из членов геометрической
прогрессии сходится при
и расходится при
.
§2. Признаки сходимости числовых рядов
Лишь в редких случаях удается получить выражение для , содержащее ограниченное число слагаемых, и непосредственно найти . Обычно, для исследования рядов на сходимость, используют признаки сходимости.
Необходимый признак сходимости ряда.
Если ряд сходится, то его общий член стремится к нулю.
Из этого признака
непосредственно вытекает, что, например,
ряд
![]() расходится, так как его общий член не
стремится к нулю,
расходится, так как его общий член не
стремится к нулю,
![]() .
Однако, следует отметить, что стремление
к нулю общего члена к нулю является лишь
необходимым признаком сходимости, но
не является достаточным. Например, общий
член ряда
.
Однако, следует отметить, что стремление
к нулю общего члена к нулю является лишь
необходимым признаком сходимости, но
не является достаточным. Например, общий
член ряда
![]() стремится к нулю,
стремится к нулю,
![]() ,
а сам ряд является расходящимся.
,
а сам ряд является расходящимся.
Ряд
![]() называется
гармоническим.
Полезно запомнить, что гармонический
ряд расходится.
называется
гармоническим.
Полезно запомнить, что гармонический
ряд расходится.
Свойства сходящихся рядов.
1. Ряд не может иметь двух различных сумм.
2. Если ряд сходится, то и любой ряд, полученный из него группировкой слагаемых, сходится и имеет ту же сумму, что и исходный.
3. Если ряды
и
![]() сходятся, то сходится и ряд
сходятся, то сходится и ряд
![]() ,
причем
+
=
.
,
причем
+
=
.
4. Если ряд
сходится, то сходится и ряд
![]() ,
где
,
где
![]() ,
причем
,
причем
![]() =
.
=
.
Далее сформулируем признаки сравнения.
Первый признак
сравнения.
Пусть даны
два ряда
и
,
члены которых неотрицательны, причем
для всех n
выполняется неравенство
![]() .
Тогда
.
Тогда
1) если сходится
ряд
,
то сходится и ряд
![]() ,
,
2) если расходится ряд , то расходится и ряд .
Пример 2.1.
Исследовать на сходимость ряд
![]() .
.
Решение.
Очевидно, что для любого n=1,
2, … справедливо неравенство
![]() .
Сравним исходный ряд с рядом
.
Сравним исходный ряд с рядом
![]() ,
составленным из членов геометрической
прогрессии с основанием
,
составленным из членов геометрической
прогрессии с основанием
![]() .
Поскольку ряд
сходится и для всех n
,
то по первому признаку сравнения, ряд
сходящийся.
.
Поскольку ряд
сходится и для всех n
,
то по первому признаку сравнения, ряд
сходящийся.
Второй признак
сравнения. Пусть
даны два ряда
и
,
члены которых неотрицательны и пусть
существует конечный предел
![]() .
Тогда при
.
Тогда при
![]() оба ряда одновременно сходятся, либо
одновременно расходятся. Если же
оба ряда одновременно сходятся, либо
одновременно расходятся. Если же
![]() ,
то из сходимости ряда
вытекает
сходимость ряда
,
а из расходимости ряда
— расходимость ряда
.
,
то из сходимости ряда
вытекает
сходимость ряда
,
а из расходимости ряда
— расходимость ряда
.
Пример 2.2.
Исследовать
на сходимость ряд
![]() .
.
Решение.
Сравним данный ряд с гармоническим
рядом
![]() .
Вычислим предел
.
Вычислим предел
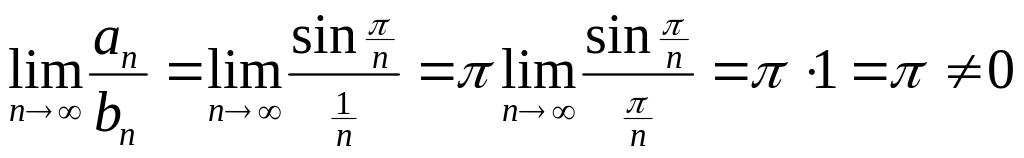 .
.
Согласно второму признаку сравнения ряды и сходятся или расходятся одновременно. Поскольку гармонический ряд является расходящимся, то и ряд расходится.
Признак Даламбера.
Пусть все
члены ряда
положительны и пусть существует предел
отношения последующего члена к
предыдущему:
![]() .
Тогда
.
Тогда
1) если
![]() ,
то ряд сходится;
,
то ряд сходится;
2) если
![]() ,
то ряд расходится;
,
то ряд расходится;
3) если
![]() ,
то ряд может как сходится, так и расходится.
,
то ряд может как сходится, так и расходится.
Пример 2.3.
Исследовать на сходимость ряд
![]() .
.
Решение. Вычислим предел отношения последующего члена к предыдущему: :
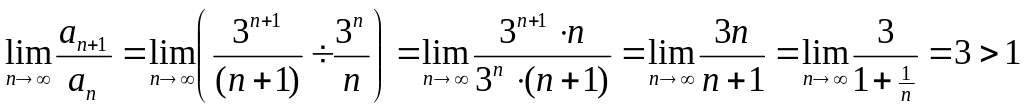 .
.
По признаку Даламбера заключаем, что ряд расходится.
Пример 2.4.
Исследовать
на сходимость ряд![]() .
.
Решение.
Применим признак Даламбера. Так как
![]() ,
,
![]() ,
то
,
то
![]() и
и
![]() .
.
Так как
![]() ,
то ряд сходится.
,
то ряд сходится.
Радикальный
признак Коши.
Пусть все
члены ряда
положительны и пусть существует предел
![]() .
Тогда
.
Тогда
1) если , то ряд сходится;
2) если , то ряд расходится;
3) если , то ряд может как сходится, так и расходится.
Пример 2.5.
Исследовать
на сходимость ряд
![]() .
.
Решение. Вычислим предел
![]() .
.
Согласно радикальному признаку Коши, ряд сходится.
Пример 2.6.
Исследовать
на сходимость ряд
![]() .
.
Решение. Применим радикальный признак Коши.
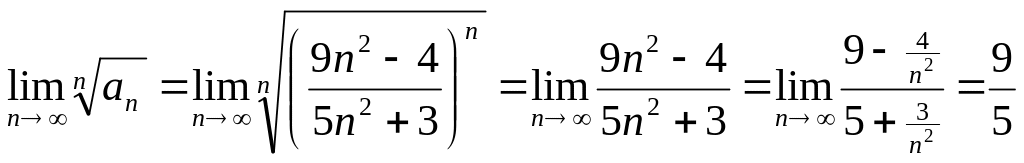 .
.
Так как
![]() ,
то ряд расходится.
,
то ряд расходится.
Интегральный
признак Коши. Пусть
функция
![]() определена, непрерывна, положительна
и монотонно убывает на луче
определена, непрерывна, положительна
и монотонно убывает на луче
![]() и стремится к нулю при
и стремится к нулю при
![]() .
Пусть
.
Пусть
![]() и
и
![]() .
Тогда числовой ряд
сходится в том и только в том случае,
если сходится несобственный интеграл
.
Тогда числовой ряд
сходится в том и только в том случае,
если сходится несобственный интеграл
![]() .
.
Пример 2.7.
Исследовать на сходимость ряд
![]() ,
,
![]() .
.
Решение. Рассмотрим
функцию
![]() .
Она определена, непрерывна, положительна
и монотонно убывает на луче
,
причем
стремится к нулю при
.
Таким образом функция
полностью удовлетворяет условиям
интегрального признака Коши и,
следовательно ряд
будет сходиться в том и только в том
случае, если сходится несобственный
интеграл
.
Она определена, непрерывна, положительна
и монотонно убывает на луче
,
причем
стремится к нулю при
.
Таким образом функция
полностью удовлетворяет условиям
интегрального признака Коши и,
следовательно ряд
будет сходиться в том и только в том
случае, если сходится несобственный
интеграл
![]() .
.
Вычислим несобственный
интеграл при
![]() .
.
![]() ,
,
то есть интеграл расходится.
Вычислим несобственный
интеграл при
![]() .
.
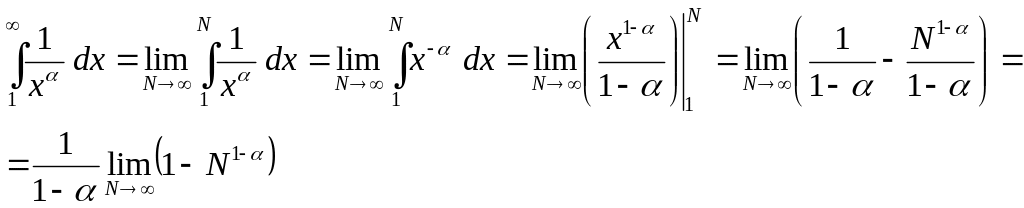
Если
![]() ,
то
,
то
![]() и интеграл
расходится.
и интеграл
расходится.
Если
![]() ,
то
,
то
![]() и
и
![]() ,
то есть интеграл
сходится.
,
то есть интеграл
сходится.
Итак, интеграл
расходится при
![]() и сходится при
.
Согласно интегральному признаку Коши,
ряд
,
расходится при
и сходится при
.
и сходится при
.
Согласно интегральному признаку Коши,
ряд
,
расходится при
и сходится при
.
Ряд называется обобщенным гармоническим рядом.
Пример 2.8.
Исследовать
на сходимость ряд
![]() .
.
Решение. Применим интегральный признак Коши. Для этого рассмотрим несобственный интеграл
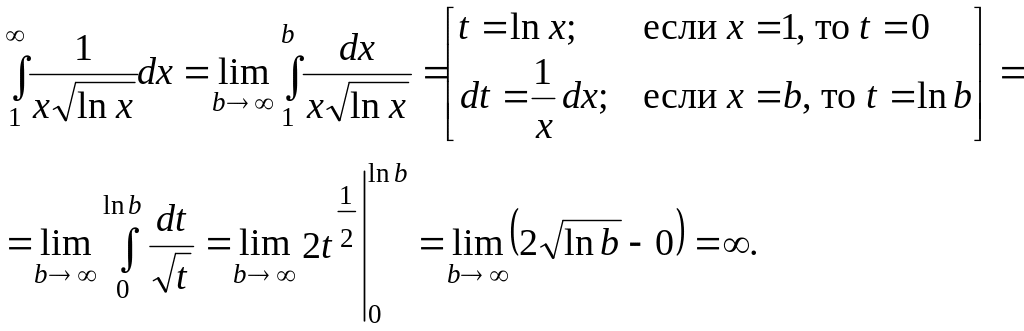
Так как соответствующий интеграл расходится, то расходится и ряд.
