Лабораторная работа № 2 Метод Гаусса для решения систем линейных алгебраических уравнений (слау)

Порядок выполнения работы

Работа выполняется в несколько этапов, а именно:

а) для получения задания обратитесь к преподавателю или нажмите кнопку НАЧАЛЬНЫЕ ДАННЫЕ;

б) в ПОЛЕ ДЕЯТЕЛЬНОСТИ (голубые ячейки) внесите расчётные формулы метода;

в) в ПОЛЕ ОТВЕТОВ (ячейки диапазона D5:D7) внесите формулы, ссылающиеся на адреса из ПОЛЯ ДЕЯТЕЛЬНОСТИ, содержащие решение задачи;

г) для проверки правильности выполнения работы нажмите кнопку РЕЗУЛЬТАТЫ.

Метод Гаусса для решения систем линейных алгебраических уравнений

Теоретические основы метода

Метод Гаусса рассмотрим на примере системы, состоящей из трех уравнений с тремя неизвестными:

(2.1)

где x₁, x₂, x₃ - неизвестные, a_ij - коэффициенты при неизвестных, b_i - свободные члены, i, j = 1, 2, 3.

В матричной форме система (2.1) может быть записана в виде

A x = B. (2.2)

Если рассматриваемая система имеет вид

(2.3)

то решения могут быть найдены по формулам

(2.4)

Суть метода Гаусса состоит в приведении системы (2.1) к виду (2.3) с последующим вычислением корней по формулам (2.4). При приведении системы (2.1) к виду (2.3) будут использованы известные факты из математики, а именно: корни системы не меняются при умножении обеих частей уравнения на одно и то же число, отличное от нуля; при сложении уравнений системы; при перестановке уравнений (строк). Будем предполагать, что на главной диагонали матрицы А отсутствуют нулевые элементы

a_ii  0, i = 1,2,3. (2.5)

Действительно, выполнение условий (2.5) всегда может быть обеспечено путём использования упомянутых выше свойств.

В качестве первой ведущей строки примем первое уравнение, а в качестве первого ведущего элемента - элемент a₁₁. Затем умножим второе уравнение системы на элемент a₁₁ и вычтем из него первое ведущее уравнение, умноженное на элемент a₂₁. Умножим третье уравнение на элемент a₁₁ и вычтем из него первую ведущую строку, умноженную на элемент a₃₁. Тогда, записывая результат в виде расширенной матрицы коэффициентов системы, получим

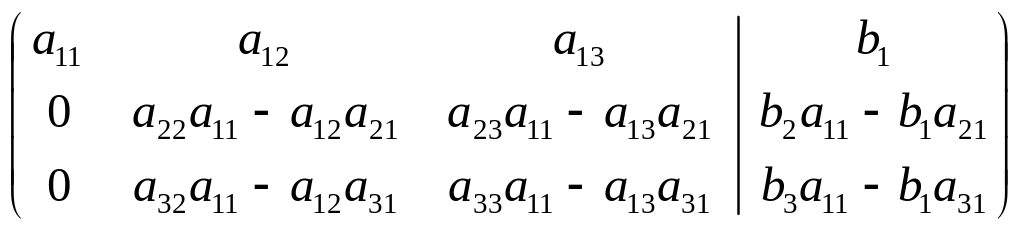
или, вводя новые обозначения,

.

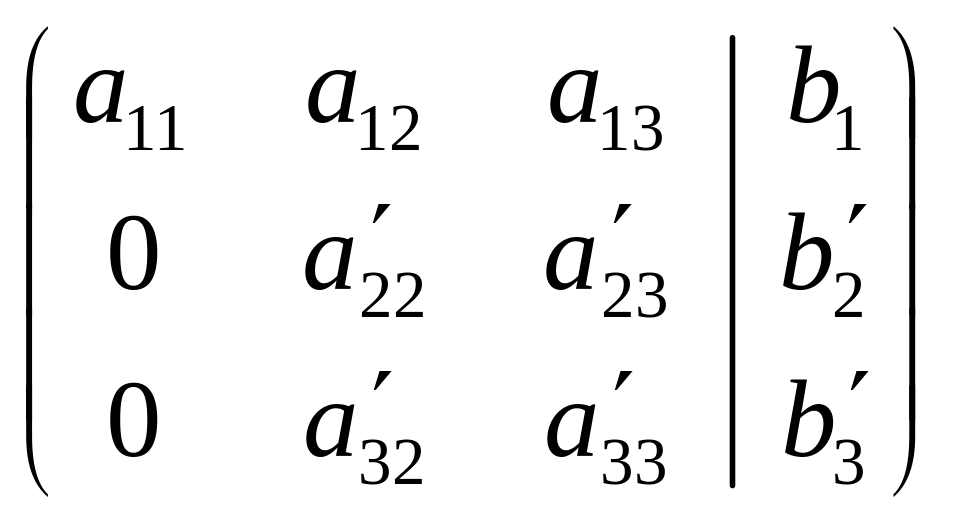В качестве второй ведущей строки выберем вторую строку полученной расширенной матрицы коэффициентов. В качестве второго ведущего элемента выберем элемент . Из третьей строки, умноженной на ведущий элемент , вычтем вторую ведущую строку, умноженную на элемент . Тогда получим

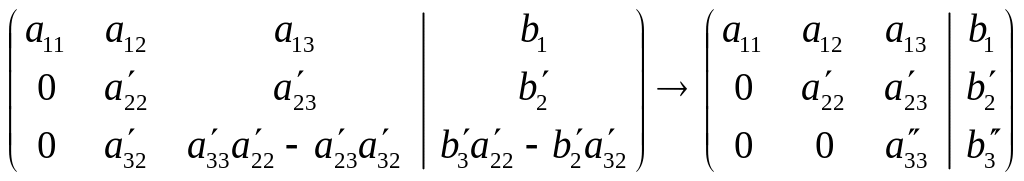. (2.6)

Полученной расширенной матрице (2.6) по форме соответствует система вида (2.3), решения которой могут быть найдены по формулам (2.4), которые и будут являться решениями исходной задачи (2.1).

В рассмотренном способе были получены нулевые элементы в матрице А, расположенные ниже главной диагонали. Аналогичным образом нули могут быть получены выше главной диагонали, выше или ниже побочной диагонали матрицы А. При этом соотношения (2.4) изменятся лишь по форме, но не по содержанию.

Лабораторная работа № 3 Итерационные методы решения слау

Порядок выполнения работы

Работа выполняется в несколько этапов:

а) для получения задания обратитесь к преподавателю или нажмите кнопку НАЧАЛЬНЫЕ ДАННЫЕ;

б) внесите начальные приближения в ячейки диапазона В21:В23;

в) внесите точность в ячейку В24;

г) в ПОЛЕ ДЕЯТЕЛЬНОСТИ (голубые ячейки) внесите расчётные формулы метода;

д) в ПОЛЕ ОТВЕТОВ (ячейки диапазона D5:D7) внесите формулы, ссылающиеся на адреса из ПОЛЯ ДЕЯТЕЛЬНОСТИ, содержащие решение задачи;

е) для проверки правильности выполнения работы нажмите кнопку РЕЗУЛЬТАТЫ.