ресует, насколько «справедливо» удовлетворяются за­явки, а важно только «подешевле развезти» имеющие­ся запасы (все равно, куда), то можно ввести в рас­смотрение фиктивный пункт отправления Aф, условно приписав ему недостающий запас, равный Подробнее на этих вопросах мы останавливаться не будем (см. [6]).

§ 11. Задачи целочисленного программирования.

Понятие о нелинейном программировании

На практике часто встречаются задачи, совпада­ющие по постановке с задачами линейного програм­мирования, но отличающиеся той особенностью, что искомые значения переменных непременно должны быть целыми. Такие задачи называются задачами целочисленного программирования; допол­нительное условие целочисленности переменных суще­ственно затрудняет их решение.

Рассмотрим пример такой задачи. Пусть имеется ряд предметов (ценностей) П1, П2, ..., Пn, которые же­лательно увезти из угрожаемого района. Известны сто­имости этих предметов: c1 c2,…cn и их веса q1, q2,…qn. Количество и вид предметов, которые мы можем увезти, лимитируется грузоподъемностью Q машины. Требуется из всего набора предметов выбрать наиболее ценный набор (с максимальной суммарной стоимостью предметов), вес которого укладывается в Q.

Введем в рассмотрение переменные х1, х2, ...xn определяемые условием: хi = 1, если мы берем в ма­шину предмет Пi, и хi = 0,— если не берем.

При заданных значениях х1, х2, ...xn суммарный вес предметов, которые мы берем в машину, равен Условие ограниченной грузо­подъемности запишется в виде неравенства:

(11.1)

Теперь запишем общую стоимость предметов, кото­рую мы хотим максимизировать:

(11.2)

Таким Образом, задача на вид почти не отличается от обычной задачи линейного программирования: най­ти неотрицательные значения переменных х1, х2, ...xn которые удовлетворяют неравенству (11.1) и обращают в максимум линейную функцию этих пере­менных (11.2). На первый взгляд может показаться, что и решать ее надо как задачу линейного програм­мирования, введя дополнительные ограничения-нера­венства (каждый предмет — только один!):

Ничуть не бывало! Найденное таким образом реше­ние может оказаться не целым, а дробным, а значит неосуществимым (не можем же мы погрузить в маши­ну треть рояля и половину шкафа!). Наша задача от­личается от обычной задачи линейного программиро­вания: она представляет собой задачу целочислен­ного программирования.

Вторая мысль, которая приходит в голову: а нель­зя ли решить обычную задачу линейного программи­рования и округлить полученные значения х{ до бли­жайшего из целых чисел 0 или 1? К сожалению, и так в общем случае поступать нельзя. Полученное та­ким образом решение даже может не удовлетворять ограничению (11.1), т. е. «не влезет» в данный вес Q. А если и «влезет», то может быть совсем не оптималь­ным. В отдельных случаях такое округление допусти­мо; например, если мы в задаче 3 § 7 получим ответ: «производством ткани первого вида надо занять 185,3 станков первого типа», то, разумеется, мы без зазре­ния совести округлим это решение до 185. Если же идет речь о ресурсах неделимых (особо ценных или же уникальных), то задачу надо ставить как задачу цело­численного программирования.

Надо заметить, что вообще задачи целочисленного программирования гораздо труднее, чем обычные за­дачи линейного программирования. На практике при­меняется ряд методов решения подобных задач; все они (при сколько-нибудь значительном числе перемен­ных) очень сложны и трудоемки. Мы не будем пытать­ся излагать эти методы здесь, а отошлем интересующе­гося читателя к более подробным руководствам (на­пример, [7, 8]).

t

В заключение скажем несколько слов о задачах не- линейного программирования.

Общая постановка задачи нелинейного программи- рования следующая. Найти неотрицательные значения переменных х1, х2, ...xn удовлетворяющие каким-то ограничениям произвольного вида, например

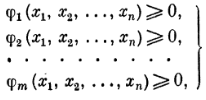(11.3)

и обращающие в максимум произвольную нелинейную функцию этих переменных:

(11.4)

Общих способов решения задачи нелинейного про­граммирования не существует; в каждой конкретной задаче способ выбирается в зависимости от вида функ­ции W и накладываемых на элементы решения огра­ничений.

Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут не пропорционально количеству закупленных или произведенных товаров (эффект «оптовости»), но многие нелинейные задачи могут быть приближен­но заменены линейными (линеаризованы), по крайней мере в области, близкой к оптимальному решению. Ес­ли это и невозможно, все же обычно нелинейные зада­чи, возникающие на практике, приводят к сравнитель­но «благополучным» формам нелинейности. В част­ности, нередко встречаются задачи «квадратичного программирования», когда W есть полином 2-й степе­ни относительно переменных х1, х2, ...xn, а неравен­ства (11.3) линейны (см. [7, 8]). В ряде случаев при решении задач нелинейного программирования может быть с успехом применен так называемый «метод штрафных функций», сводящий задачу поиска экстре­мума при наличии органичений к аналогичной задаче при отсутствии ограничений, которая обычно решается проще. Идея метода состоит в том, что вместо того, чтобы наложить на решение жесткое требование вида φ(х1, х2, ...xn)≥0, можно наложить некоторый дос­таточно большой «штраф» за нарушение этого условия и добавить к целевой функции W(х1, х2, ...xn) штраф вида аφ(х1, х2, ...xn),где а — коэффициент пропорциональности (в случае, когда целевая функция максимизируется, а отрицательно, если минимизируется положительно). Далее можно, увеличивая абсолютное значение а, посмотреть, как изменяется при этом оптимальное решение (х*1, х*2, ... x*n) практически перестает меняться, остановиться на нем. В ряде случаев при решении задач нелинейного про­граммирования оказываются полезными так называе­мые «методы случайного поиска», состоящие в том, что вместо упорядоченного перебора возможных вари­антов решения применяется случайный розыгрыш. Со всеми этими методами (и некоторыми другими) чита­тель в случае надобности может ознакомиться по ру­ководствам [7—9].

В последнюю очередь упомянем о так называемых задачах стохастического программирова­ния. Особенность их в том, что ищется оптимальное решение в условиях неполной определенности, когда ряд параметров, входящих в целевую функцию W, и ог­раничения, накладываемые на решение, представляют собой случайные величины. Такое программирование называется стохастическим. Существуют задачи, где стохастическое программирование сводится к обычному, детерминированному. Например, когда оптимизация производится «в среднем», целевая функция W линей­но зависит от элементов решения, случайны только коэффициенты при элементах решения, а накладывае­мые условия не содержат случайности. Тогда можно оп­тимизировать решение, забыв о случайном характере коэффициентов и заменив их математическими ожида­ниями (ибо, как вы знаете, математическое ожидание линейной функции равно той же линейной функции от математических ожиданий аргументов). Гораздо более серьезен случай, когда на элементы решения наклады­ваются стохастические ограничения. Проблемы стохас­тического программирования довольно полно освещены в монографии [31].

В отличие от задач линейного программирования, методы решения которых хорошо отлажены, устоялись и не представляют существенных трудностей, задачи целочисленного, нелинейного и особенно стохастиче­ского программирования принадлежат к сложным и трудным вычислительным задачам. При их решении часто приходится прибегать к приближенным, так на­зываемым «эвристическим» методам оптимизации, так как точные методы по своей трудоемкости оказываются неподъемными даже для современной вычислительной техники. Бывает так, что весь выигрыш, который был бы получен от точной оптимизации решения, «съеда­ется» затратами на получение этого решения, так что «игра не стоит свеч». Здесь опять мы встречаемся с необходимостью «системного» подхода к задачам ис­следования операций, учета не только непосредствен­ного выигрыша в данной операции, но и затрат на ее оптимизацию.

Правда, возможности вычислительной техники I (быстродействие, объем памяти) с течением времени растут, и то, что невыгодно экономически сегодня, мо­жет сделаться выгодным завтра. С другой стороны, па­раллельно с ростом возможностей вычислительной техники растет и сложность оптимизационных задач, ко­торые приходится решать. Не надо забывать, что принятие того или иного способа оптимизации решения есть тоже «решение», и иной раз весьма ответственное.