
- •Раздел 1. Техническая механика. Тема 1. Введение в основы технической механики.
- •1.1. Статика и ее основные понятия и определения.
- •1.2. Аксиомы статики
- •1.3. Система сходящихся сил.
- •1.3.2. Связи и их реакции
- •Тема 2. Кинематика.
- •2.2. Основные кинематические способы определения движения точки
- •2.2.2. Координатный способ
- •2.3. Частные случаи движения точки
- •2.4. Динамика поступательного и вращательного движения
- •2.4.6.Разложение движения плоской фигуры в ее плоскости на поступательное и вращательное. Уравнения движения.
- •Тема 3. Динамика.
- •3.1. Основные аксиомы динамики
- •3.2. Метод кинетостатики
- •3.3. Работа при поступательном движении
- •3.6. Понятие о трении и коэффициенте полезного действия
- •3.8. Потенциальная и кинетическая энергия
- •3.10. Закон изменения кинетической энергии
- •3.7. Закон количества движения
- •3.9. Моменты инерции некоторых однородных тел
- •3.4. Мощность
- •2. Мощность, развиваемая двигателем лесовоза, будет
- •3.5. Работа и мощность при вращательном движении Работа.
- •3.4. Мощность
- •2. Мощность, развиваемая двигателем лесовоза, будет
- •3.5. Работа и мощность при вращательном движении Работа.
- •Тема 4. Сопротивление материалов.
- •4.3.2. Расчет на жесткость
- •4.6. Сложные виды деформаций
- •4.4.1. Расчет на прочность
- •4.5. Плоский изгиб
- •4.5.1. Внутренние силовые факторы
- •4.6. Динамические нагрузки. Удар 4.6.1.
- •3.6.2. Расчет на удар
- •Тема 5. Детали машин.
- •6. Тракторы и автомобили
- •Раздел 2. Тракторы и автомобили.
- •Тема 6. Общее устройство тракторов и автомобилей.
- •6.3. Классификация автомобилей
- •Тема 7. Обще устройство и работа двигателей внутреннего сгорания.
- •Тема 8. Кривошипно-шатунный механизм.
- •Тема 9. Механизм газораспределения.
- •Тема 10. Основные системы двигателя внутреннего сгорания
- •Тема 11. Трансмиссия тракторов и автомобилей.
- •Тема 12. Ходовая часть и управление тракторов и автомобилей.
- •Тема 13. Трактора и машины, используемые на лесохозяйственных работах.
4.3.2. Расчет на жесткость
Рассмотрим продольную деформацию стержня, изображенного на рис. 3.11. Для этого выделим из стержня бесконечно малый элемент длиной d z. Штриховыми линиями он показан в деформированном состоянии: длина элемента увеличилась, а размеры поперечного сечения уменьшились. Приращение длины элемента обозначим Δ(d z). Отношение приращения (изменения) длины элемента к его первоначальной длине называется относительным удлинением или продольной деформацией:
εпр= Δ(d z). / dz (3.15)
Это безразмерная величина. В некоторых случаях ее выражают в %. При растяжении продольную деформацию считают положительной, а при сжатии — отрицательной.
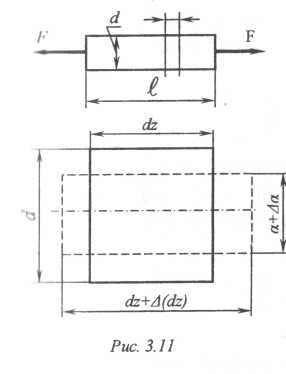
εп= Δа / а (3.16)
При растяжении поперечные размеры бруса уменьшаются и ε п по принятому правилу знаков - величина отрицательная.
Продольную и поперечную деформацию называют также линейными деформациями (общее наименование). Опытным путем установлено, что при простом растяжении или сжатии отношение поперечной деформации к продольной - величина постоянная для данного материала. Это отношение, взятое по абсолютному значению, называется коэффициентом поперечной деформации или коэффициентом Пуассона : μ=ε п / εпр
Значения коэффициента Пуассона для различных материалов находятся в пределах от 0 (для пробки) до 0,5 (для каучука). Для большинства металлов и сплавов его значение колеблется в сравнительно узких пределах: от 0,23 до 0,35 (в среднем примерно 0,3).
Определим изменение длины (удлинение или укорочение) бруса. Из выражения продольной деформации имеем Δ(d z) = εпр ■ dz - изменение длины бесконечно малого элемента, а из выражения закона Гука при линейной деформации
ε пр= σ/ Е и Δ(dz) =εnp* dZ = εdz/ E.
Учитывая, что нормальное напряжение в поперечном сечении бруса σ= N / A получаем:
(3-18)
Для определения изменения длины Δl всего бруса (или участка бруса) следует просуммировать значения Δ(dz) по всей длине.
4.4. Кручение стержня круглого сечения
4.4.1 Напряжения и деформации при кручении
 Зная,
что при кручении происходит деформация
сдвига, естественно считать, что в точках
поперечного сечения бруса возникают
только касательные напряжения τ,
перпендикулярные радиусу, соединяющему
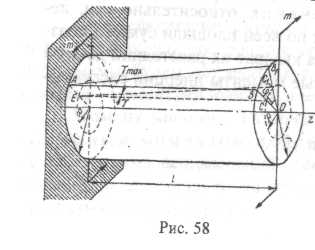
эти точки с осью кручения. Точка С (рис.
58) поперечного сечения бруса до деформации,
лежащая на некоторой образующей ЕС,
проведенной внутри на расстоянии р от
его оси, под действием момента т, смещается
и положение ЕС1. Сдвиг СС1 характеризуется
углом у, поэтому можно записать:
Зная,
что при кручении происходит деформация
сдвига, естественно считать, что в точках
поперечного сечения бруса возникают
только касательные напряжения τ,
перпендикулярные радиусу, соединяющему
эти точки с осью кручения. Точка С (рис.
58) поперечного сечения бруса до деформации,
лежащая на некоторой образующей ЕС,
проведенной внутри на расстоянии р от
его оси, под действием момента т, смещается
и положение ЕС1. Сдвиг СС1 характеризуется
углом у, поэтому можно записать:
СС1 =l*tgγ.
Однако, в силу незначительности деформаций можно записать, что γ = tg γ, тогда
СС1=lγ.
С другой стороны, дугу СС\ можно выразить как центральную дугу, соответствующую углу поворота φ, т.е.
СС, = рφ.
Приравнивая оба значения дуги ССХ получим
l γ = рφ,
откуда γ = рφ / l, т.е.
угол сдвига в поперечном сечении прямо пропорционален расстоянию от оси кручения.
При р = г угол сдвига принимает максимальное значение и имеет вид γ max = rφ / l
4.5. Изгиб
Основные понятия. Поперечная сила и изгибающий момент
При изгибе поперечные сечения, оставаясь плоскими, поворачиваются относительно друг друга вокруг некоторых осей, лежащих в их плоскостях. На изгиб работают балки, оси, валы и другие детали и элементы конструкций.
На практике встречаются поперечный (прямой), косой и чистый виды изгиба.
Поперечным (прямым) (рис. а) называется изгиб, когда
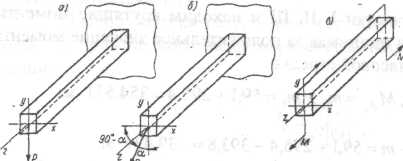
внешние силы, перпендикулярные продольной оси балки, действуют в плоскости, проходящей через ось балки и одну из главных центральных осей ее поперечного сечения.
Косой изгиб (рис., б) это изгиб, когда силы действуют в плоскости, проходящей через ось балки, но не проходящей ни через одну из главных центральных осей ее поперечного сечения.
В поперечных сечениях балок при изгибе возникают два вида внутренних сил - изгибающий момент М„ и поперечная сила Q. В частном случае, когда поперечная сила равна нулю, а возникает только изгибающий момент, то имеет место чистый изгиб (рис. в). Чистый изгиб возникает при нагружении распределенной нагрузкой или при некоторых нагружениях сосредоточенными силами, например, балка, нагруженная двумя симметричными равными силами.
При изучении деформации изгиба мысленно представляется, что балка состоит из бесконечного количества волокон, параллельных продольной оси. При чистом изгибе справедлива гипотеза плоских сечений: волокна, лежащие на выпуклой стороне растягиваются, лежащие на вогнутой стороне — сжимаются, а на границе между ними лежит нейтральный слой волокон (продольная ось), которые только искривляются, не изменяя своей длины; продольные волокна балки не оказывают друг на друга давления и, следовательно, испытывают только растяжение и сжатие.
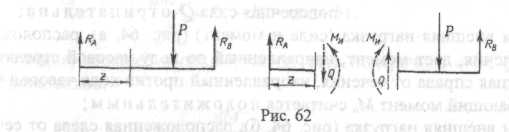
Внутренние силовые факторы в сечениях балок - поперечная сила Q и изгибающий момент Ми (рис. 62) зависят от внешних сил и изменяются по длине балки. Законы изменения поперечных сил и изгибающих моментов представляются некоторыми уравнениями, в которых аргументами
являются координаты z поперечных сечений балок, а функциями - Q и Ми. Для определения внутренних силовых факторов применим метод сечений.
Поперечная сила Q есть равнодействующая внутренних касательных сил в поперечном сечении балки. Следует иметь в виду, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики.
Изгибающий момент Ми есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечения балки. Изгибающий момент также, как и поперечная сила имеет разное направление для левой и правой части балки. Это говорит о непригодности правила знаков статики при определении знаков изгибающего момента.
Рассматривая равновесие частей балки, расположенных слева и справа от сечения, видно, что в поперечных сечениях должны действовать изгибающий момент Ми и поперечная сила Q. Таким образом, в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.
Для наглядного изображения распределения вдоль оси балки поперечных сил Q и изгибающих моментов Ми удобно представлять их в виде эпюр, ординаты которых для любых значений абсциссы z дают соответствующие значения Q и Ми. Эпюры строятся аналогично построению эпюр продольных сил (см. 4.4) и крутящих моментов (см. 4.6.1.).
Так как для установления знаков поперечных сил и изгибающих моментов правила знаков статики неприемлемы, установим для них другие правила знаков, а именно, если внешние силы (рис. а), лежащие по левую сторону от сечения, стремятся приподнять левую часть балки или, лежащие по правую сторону от сечения, опустить правую часть балки, то поперечная сила Q
- если внешние силы (рис. 63, б), лежащие по левую сторону от сечения, стремятся опустить левую часть балки или, лежащие по правую сторону от сечения, приподнять правую часть балки, то поперечная сила Q отрицательна;
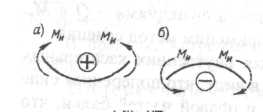
- если внешняя нагрузка (сила и момент) (рис. 64, а), расположенная слева от сечения, дает момент, направленный по ходу часовой стрелки или, расположенная справа от сечения, направленный против хода часовой стрелки, то изгибающий момент Ми считается положительным;
Правило знаков для изгибающих моментов связано с характером деформации балки. Изгибающий момент считается положительным, если балка изгибается выпуклостью вниз (растянутые волокна расположены внизу). Изгибающий момент считается отрицательным, если балка изгибается выпуклостью вверх (растянутые волокна расположены вверху).
Пользуясь правилами знаков, следует максимально представлять себе сечение балки жестко защемленным, а связи — отброшенными и замененными их реакциями. Для определения реакций пользуются правилами знаков статики.
