3.4. Вычисление объема тела вращения.
Пусть тело образовано вращением вокруг оси Ох криволинейной трапеции, заданной непрерывной функцией y = f (x) на [a, b]. Тогда объем тела вращения вычисляется по формуле
. (3.4.1)
Замечание. Если криволинейная трапеция 0 х (у), а у b вращается вокруг оси Оу, то объем тела вращения вычисляется по
формуле
(3.4.2)
3.5. Вычисление поверхности вращения.
Пусть функция f(x) неотрицательна и непрерывна вместе со своей производной на отрезке [a; b]. Тогда поверхность, образованная вращением графика этой функции вокруг оси Ох имеет площадь S, которая может быть вычислена по формуле
(3.5.1)
§4. Несобственные интегралы.
Рассмотренное
ранее понятие определенного интеграла
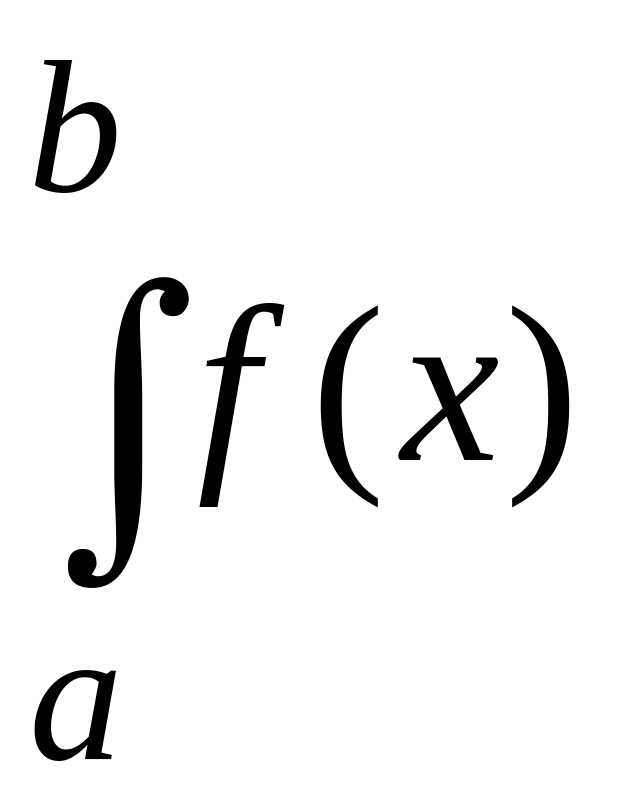dx
дано для
случая, когда пределы интегрирования
a и b − числа
конечные, а подынтегральная функция
f(x)
– непрерывная на отрезке [a;
b].
В этом случае такой интеграл называют
еще собственным
интегралом.
Определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования называют несобственным интегралом первого рода.
4.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл ι рода).
Пусть функция f(x)
непрерывна на промежутке [a;
).
Если существует конечный предел
,
то его называют несобственным
интегралом первого рода
и обозначают
.
Таким образом, по
определению 
=
В этом случае говорят, что несобственный интеграл сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл расходится.
Аналогично
определяется несобственный интеграл
на промежутке (−
;
b]:
=
.
Несобственный интеграл с двумя бесконечными пределами определяется формулой
=
+
,
где с – произвольное число.
В этом случае интеграл слева сходится тогда и только тогда, когда сходятся оба интеграла справа.
Замечание. Если непрерывная функция f(x) ≥ 0 на промежутке [a; ) и интеграл сходится, то он выражает площадь бесконечно длинной криволинейной трапеции (см. рис. 10)
П
римеры.
Вычислить несобственные интегралы или
установить их расходимость.
1)
;
2)
.
Решение
1)
=
=
=
− (0 – 1) = 1, интеграл сходится.
2)
=
=
=
=
=
,
интеграл расходится.
Признаки сходимости для несобственных интегралов первого рода.
Теорема 4.1.1 (признак сравнения).
Если на промежутке
[a;
)
непрерывные функции f(x) и
(х)
удовлетворяют условию 0 ≤ f(x) ≤
(х),
то из сходимости интеграла
следует сходимость интеграла
,
а из расходимости интеграла
следует расходимость интеграла
.
Пример.
Исследовать сходимость интеграла
.
Решение
При х ≥ 1 имеем
<
.
Но интеграл
= 1 сходится (см. пример 1).
Следовательно, интеграл также сходится и, кроме того, его значение меньше 1.
Теорема 4.1.2.
Если существует предел
,
0<k<
,
(f(x)>0,
(х)>0),
то интегралы
и
одновременно оба сходятся или расходятся
(т.е. ведут себя одинаково в смысле
сходимости).
Пример.
Исследовать сходимость интеграла
.
Решение
Интеграл
сходится.
Рассмотрим предел
=
=
,
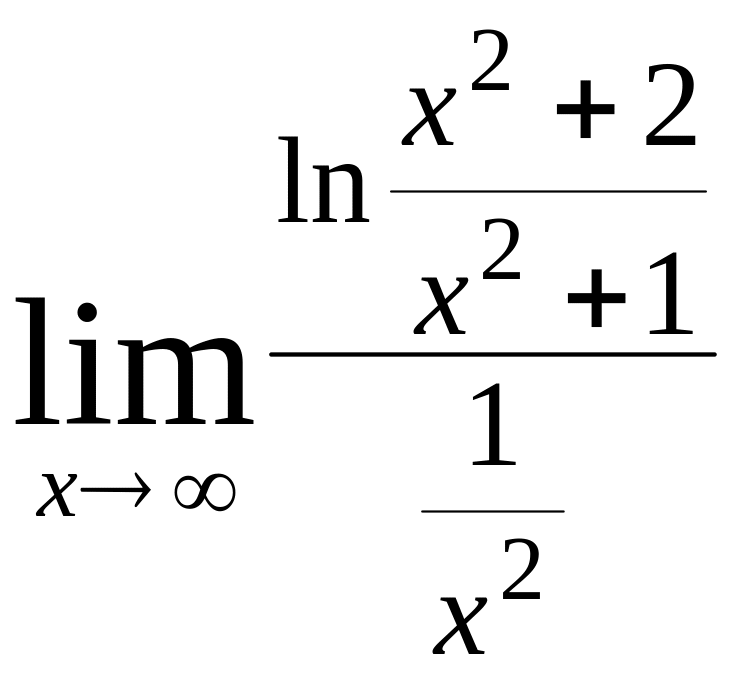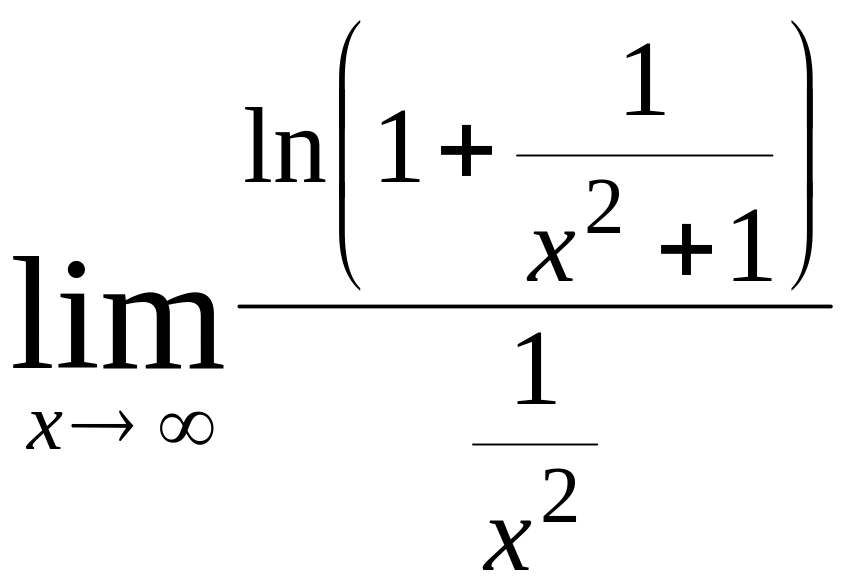Следовательно, интеграл также сходится.