6. Инварианты сетей Петри

Структура сетей Петри может обеспечивать при работе сети постоянство некоторых функций от маркировок сети. Такие функции называют инвариантами сетей Петри. Вычисление инвариантов может оказаться полезным при исследовании свойств моделируемых систем (например, при верификации тестировании программ) [10]. '

Различают инварианты позиций и инвариантыпереходов.

Для того чтобы пояснить смысл этих терминов, введем в рассмотрение п × т -матрицу

V = ||f_j ^t_i – f_i ^p_j|| = (F^t)^T – F^P,

каждый элемент которой v_ij = f_j^t_i – f_i ^p_j показывает разность между числом поступивших фишек – f _j^t_i и числом изъятых f _ij^p, т.е. изменение маркировки позиции р_i Є Р при срабатывании перехода t _j Є Т. В силу того, что f _j^t_i -. и f _ij^p - целые числа, величины v_ij также целые. В зависимости от знака v_ij при срабатывании перехода t _j в позиции p_i число фишек либо увеличивается (v_ij >0), либо уменьшается (v_ij <0), либо остается неизменным (v_ij = 0).

1. Инварианты позиций. Припишем каждой позиции р_i Є Р некоторый вес и_i , который может принимать целочисленные значения - положительные, отрицательные нулевые. Эти веса образуют п - вектор-строку.

Рассмотрим m - вектор-строку Y = U · V и определим условия, при которых этот вектор является нулевым, т.е.

Y= Û · V = Ø_m , (2.10)

где Ø_m - m-вектор-строка, состоящая из нулей; Û - ненулевой n - вектор.

Представим матрицу V в виде п – столбца

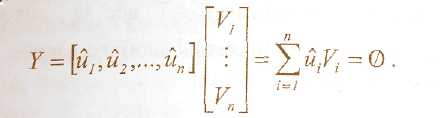
где Vi – вектор-строка. Тогда условие (2.10) может быть представлено в виде

Отсюда следует, что условие (2.10) при Û≠0 может выполняться только в том случае, если среди строк Vi матрицы V найдутся линейные независимые строки.

Пусть для простоты имеются две такие строки с номерами k и l – Vk и Vi, которые соответствуют в матрице V позициям рk и р, и пусть соответствующие веса не равны нулю: uk ≠0, ul ≠0. Веса остальных позиций положим равными нулю: ui = 0 при i ≠ k, i ≠ l. В силу линейной зависимости строк k и l веса u и u можно подобрать таким образом, что

ûkVk+ûlVl=Øm;ûlvlj+ûlvlj=0,j=1,…..,m. (2.11)

Таким образом, вектор Û имеет вид

Û= [ 0,…..,0, ûk, 0,….,0,ûl,0,….0]

и в силу (2.11) обеспечивается выполнение условия (2.10).

Подсчитываем теперь приращение числа фишек в позициях рk и р l при срабатывании перехода

t Є T. Пусть до срабатывания перехода tj маркировки в позициях рk и рl были соответственно μr и μl. После срабатывания t маркировки с учетом введенных весов ûk и ûl стали равными μ’k = μk + ûkvkj, μ’l=μl +ûlvlj, а их сумма μ’k + μ’l = μk + ûkvkj + μl + ûlvlj = μk + μl в силу (2 11). Таким образом, сумма μ_k + μ_l при учете введенных весов позиций û_k , û_l остается постоянной при срабатывании любого перехода и равна этой сумме при начальной маркировке М ₀. Построенный описанным образом вектор Û называется инвариантом позиций сети Петри.

2. Инварианты переходов. По аналогии с предыдущим разделом припишем каждому переходу t_j Є T вес w_i который может принимать целочисленные значения любого знака. Эти веса сведем в т - вектор-столбец

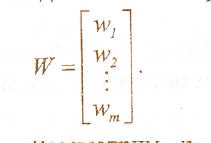
Рассмотрим п- вектор-столбец Z = V-W и условия, при которых этот вектор является нулевым, т.е.

_m

Z = V · W = [V¹,V²,…,V^m]· Ŵ = Σ V^jŵ_j = Ø_n, (2.12)

^j=1

где Ø_n - п-вектор, состоящий из пулей; Ŵ- ненулевой т-вектор; V ⁱ - i-й п -столбец матрицы V.умножив веса и, и щ на постоянное число k = const, мы Аналогично сказанному выше можно убедиться в том, что условие (2.12) выполняется только в том случае, когда среди столбцов матрицы V найдутся линейно зависимые. Пусть имеются два линейно зависимых столбца с номерами р и q, которые соответствуют переходам t_p и t_q, и пусть соответствующие веса не равны нулю, w_p≠0, w_q≠0. Остальные веса положим нулевыми: w_j = 0 при j ≠ р, j ≠ q . В силу линейной зависимости векторов V^р и V^q можно подобрать вeca w_p и w_q таким образом, чтобы выполнялось условие (2.12).

Проанализируем теперь, как будет изменяться сети при последовательном срабатывании переходов t_p и t’_q. Пусть маркировка некоторой позиции р_i до срабатывания переходов была μ_.

После срабатывания t_p она (с учетом веса ŵ_р) стала μ_{i =} μ_i + ŵ_pv_ip, а после срабатывания t_q ( с учетом веса ŵ_q ) μ_i= μ_i + ŵ_pv_ip +ŵ_qv_iq = μ_i. Таким образом, после последнего срабатывания t_p и t_q получается исходная маркировка всех позиций, i= 1,……,n.

Вектор Ŵ, удовлетворяющий условию (2.12), называется инвариантом переходов.

Приведенные рассуждения легко обобщаются и на случай, когда число линейно зависимых строк (и столбцов) в матрице V больше двух. Напомним, что число линейно независимых строк матрицы V равно числу ее линейно независимых столбцов и равно рангу матрицы V, который обозначается буквой r_v. Величина d_v = min (n,m) - r_v, называется дефектом матрицы V. Таким образом, для того чтобы можно было построить инварианты позиций и переходов сети Петри Û, Ŵ, удовлетворяющие условиям (2.10), (2.12), необходимо чтобы дефект матрицы V был больше нуля: d_v > 0.

Из сказанного вытекает также, что задача нахождения инвариантов сети Петри решается неоднозначно. Так, например, умножив веса u_k и u_l на постоянное число k=const, мы получим другой вектор-инвариант Û’ = kÛ, который обладает теми же свойствами, что и Û.

Отметим один частный случай. Если для некоторой сети Петри существует вектор-инвариант позиций Û, все элементы которого равны единице, то это означает, что при работе сети сумма фишек во всех позициях постоянна и равна этой сумме в начальной маркировке:

_n

Σμ_i (θ) = const, θ = 0,1,2,…..

ⁱ⁼¹

Такая сеть Петри, как было сказано выше, называется консервативной.

Пример. Рассмотрим сеть Петри, изображенную рисунке 2.1, и составим для нее матрицу V

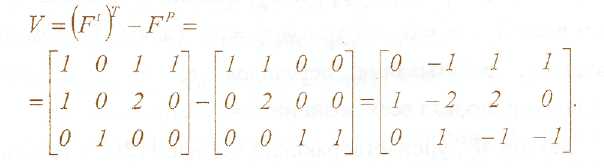
Легко видеть, что в этой матрице первая и третья строки линейно зависимы, причем достаточно взять веса û₁= 1, û₃=1, û₂=0. При этом получим вектор-инвариант по позициям Û= [1,0,1], следовательно, сумма фишек в позициях р₁ и р₃ постоянна при срабатывании любого перехода: μ₁ + μ₃= const, в чем легко убедиться, проанализировав дерево маркировок на рисунке 2.2.

Рассмотрим теперь столбцы матрицы V . Мы видим, что второй и третий столбцы линейно зависимы, при этом вектор-инвариант по переходам может быть взят следующим:

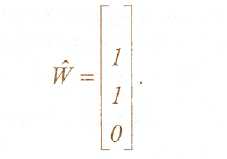
Это означает, что при последовательном срабатывании переходов t₂, t₃ (в любом порядке) маркировка сети повторяется. Это также видно на рисунке 2.2.

Инварианты для более сложной сети Петри рассматриваются в п. 3.7.