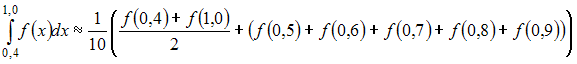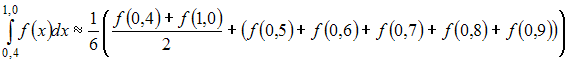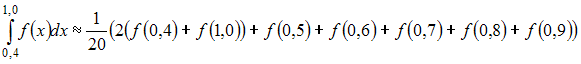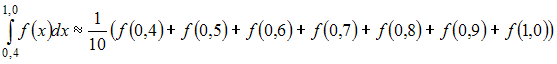- •4. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
- •6. Значение дифференцируемой функции в точке можно приближенно найти как …
- •7. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
- •16. Значение дифференцируемой функции в точке можно приближенно найти как …
- •20. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
- •22. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
- •30. Значение дифференцируемой функции в точке можно приближенно найти как …
- •33. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
- •35. Значение дифференцируемой функции в точке можно приближенно найти как …
- •37. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
- •38. Методом Эйлера с шагом решается задача Коши для системы дифференциальных уравнений с начальными условиями , . Тогда значения искомых функций и равны …
22. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. Значение определенного интеграла по формуле парабол (Симпсона) можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Воспользуемся
формулой парабол приближенного вычисления
определенного интеграла вида:
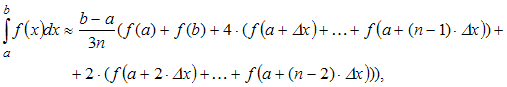 где
где
![]() Пусть
Пусть
![]() Тогда
Тогда
![]()
![]()
![]() Получаем
Получаем
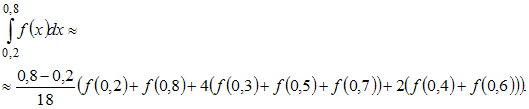
24. Значение определенного интеграла по формуле трапеций можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25. Функция представлена таблицей: Тогда график многочлена, интерполирующего эту функцию, пересекает ось в точке с абсциссой …
|
|
|
5,5 |
|
|
|
11 |
|
|
|
6 |
|
|
|
0 |
Решение:
Через
две точки проходит единственный полином
1-ой степени, графиком которого является
прямая. Для получения интерполяционного
полинома Лагранжа 1-ой степени требуются
два узла
![]() и
значения данной функции в них
и
значения данной функции в них
![]() :
:
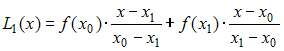 .
Подставим
в эту формулу
.
Подставим
в эту формулу
![]() :
:
![]() .
Чтобы
получить абсциссу точки пересечения
этой прямой с осью абсцисс, приравняем
.
Чтобы
получить абсциссу точки пересечения
этой прямой с осью абсцисс, приравняем
![]() к
нулю:
к
нулю:
![]() ,
то есть
,
то есть
![]() .
.
26. Интерполяционный
многочлен Лагранжа, составленный по
таблице значений функции
![]()
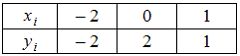 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Интерполяционный
многочлен Лагранжа 2-ой степени для
таблицы
имеет
вид:
.
В
нашем случае получим:
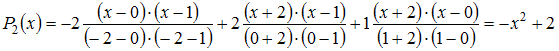 .
.
27. Методом Эйлера с шагом решается задача Коши для системы дифференциальных уравнений с начальными условиями , . Тогда значения искомых функций и равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Интерполяционный многочлен Лагранжа 2-ой степени для таблицы имеет вид: . В нашем случае получим: .
29. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Метод Эйлера решения задачи Коши , реализуется по следующим формулам: , , где – шаг расчета (величина изменения аргумента), , а – искомое решение задачи. Значения и для значения определяются начальным условием задачи Коши. В нашем случае , , , . Требуется реализовать только один шаг (этап) метода Эйлера, поскольку и . Тогда .