1). Разобьем весь промежуток времени на n произвольных интервалов

t₀ = α < t₁< t₂ < … < t_i-1 < t_i < … t_n-1 < t_n = β,

где t_i – t_i-1 = Δt_i. На произвольном участке [t_i-1, t_i] будем считать химическую реакцию близкую к равномерному с постоянной скоростью v = v(τ_i), t_i-1 ≤ τ_i ≤ t_i. Тогда за время Δt_i количество вступившего в реакцию вещества приближенно равно m_i = v(τ_i)Δt_i. Результат справедлив для каждого интервала (i = 1, 2, …, n).

2). Если указанные интервалы достаточно малы, то все количество вступившего в реакцию вещества приближенно равно сумме:

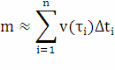
Эта формула тем точнее, чем мельче разбиение данного промежутка времени.

3). Для получения точной формулы количества вступившего в реакцию вещества перейдем к пределу, увеличивая число дроблений (n→∞) и бесконечно измельчая сами интервалы. Обозначим λ = Δt_i, тогда

В результате получим:

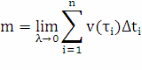
1.3 Задача о работе переменной силы

Пусть материальная точка под действием постоянной силы F перемещается по направлению этой силы. Если пройденный путь равен s, то, как известно из курса физики, работа Р этой силы F вычисляется по формуле: Р = F_S.

Пусть теперь материальная точка движется по оси Ох от точки А(а) до точки B(b) (b>a) под действием переменной силы, направленной по Ох и являющейся функцией от х: F = f(x).

Для нахождения работы Р в этом случае разобьем отрезок [a; b] точками a = x₀<x₁<…<x_n = b на n частичных отрезков и положим: Δx_i = x_i – x_i-1, i = 1, 2, ..., n. Наибольшую из этих разностей обозначим через λ = max Δx_i. Если эти отрезки достаточно малы, то без большой ошибки на каждом из них силу F можно считать постоянной (равной f(τ_i)), что дает приближенное выражение для работы

где τ_i – одна из точек сегмента [x_i-1, x_i]. Отсюда:

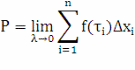
1.4 Задачи о площади криволинейной трапеции

Пусть на промежутке [a; b] задана функция f(x)≥0. Криволинейной трапецией называется плоская фигура, ограниченная указанной кривой y=f(x), прямыми x=a, x=b и осью Оx. (рис. 1). Для вычисления ее площади проделаем несколько операций.

Рисунок. 1

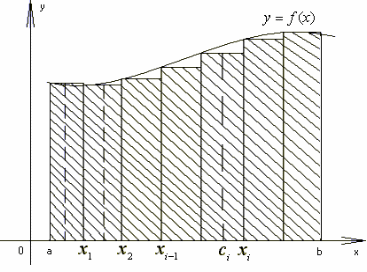
1). Разобьем промежуток [a; b] произвольными точками x₀=a<x₁<x₂<…<x_i-1<x_i<…<x_n=b на n частей. Положим Δx_i = x_i – x_i-1, то есть Δx_i есть длина i-го частичного отрезка, а наибольшую из этих длин обозначим λ, (λ=max Δx_i).

2). На каждом отрезке [x_i-1, x_i] возьмем по произвольной точке c_i,

x_i-1<c_i< x_i и вычислим f(c_i). Построим прямоугольник с основанием [x_i-1, x_i] и высотой f(c_i). Его площадь равна S_i=f(c_i)*(x_i – x_i-1). Проделаем это для каждого i = 1, 2, …, n.

3). Площадь всей заштрихованной ступенчатой фигуры, составленной из прямоугольников, равна сумме

.

Площадь S криволинейной трапеции будет приближенно равна площади ступенчатой фигуры:

Чем мельче отрезки деления, тем точнее полученная фигура “отображает” криволинейную трапецию.

4). За площадь криволинейной трапеции принимают предел, к которому стремятся площади ступенчатых фигур, когда длины отрезков деления стремятся к нулю, а их число неограниченно увеличивается (n→∞). Таким образом,

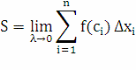
Мы рассмотрели несколько видов задач, приводящие к понятию определенного интеграла, а теперь сформулируем определения данного понятия. Возможны два различных подхода к определению определённого интеграла.

Определение 1: приращение F(b)-F(a) любой из преобразованных функций F(x)+c при изменении аргумента от x=a до x=b называют определённым интегралом от a до b функции f и обозначается .

Причём функция F является первообразной для функции f на некотором промежутке D, а числа а и b принадлежат этому промежутку. Это можно записать следующим образом:

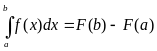
Данная формула является формулой Ньютона-Лейбница.

Определение 2:

Если при любой последовательности разбиений отрезка [a;b] таких, что δ = max Δx_i→0 (n→∞) и при любом выборе точек интегральная сумма σ_k= f(ε_i) Δx_i стремится к одному и тому же конечному пределу А, то это число А и есть определённый интеграл, т.е.

lim_n→∞ σ_k = lim_δ→0 f (ε_i) Δx_i=A(2).

Где Δх_i = x_i - x_i-1 (i=1,2,…,n) ε = max Δx_i – начало разбиения произвольная точка из отрезка [x_i-1;x_i] сумма всех произведений f(ε_i)Δx_i(i=1,…,n). Простыми словами, определенный интеграл есть предел интегральной суммы, число членов которой неограниченно возрастает, а каждое слагаемое стремится к нулю.