
Книга по ЦОС в формате pdf
.pdf
Пик-фактором ненулевого сигнала x CN называется величина
p(x) = maxj 0:N −1 |x(j)|2
1 PN −1 |x(j)|2
Nj=0
Покажем, что 1 6 p(x) 6 N . Это следует из двух очевидных неравенств
1 |
N −1 |
|
|
|
|
|
N −1 |
|
|
|
X |
2 6 max |
|
|
2 |
|
X |
|
2 |
|
x j |
x j |
)| |
|
6 |
j=0 | |
x(j) |
|
|
N |
j=0 | ( )| |
j 0:N −1 |
| ( |
|
|
| |
|
При этом первое неравенство выполняется как равенство, только когда x(j) = const для всех j Z, а второе – только тогда, когда у сигнала x на основном периоде лишь один отсчет отличен от нуля.
9.Алгоритм Витерби
Постановка задачи
В наиболее общей форме алгоритм Витерби (АВ) можно рассматри• вать, как способ решения задачи оценивания по максимуму апостериорной вероятности (МАВ) последовательности состояний дискретного марковско• го процесса с конечным числом состояний.
Марковский дискретный процесс определяется следующим образом. Состояние xk, принимаемое в момент времени k принадлежит конечному числу M состояний. Пространство состояний X можно просто обозначить {1, 2, . . . , M }. В начале предполагается, что процесс протекает на конеч• ном временном интервале от 0 до K и что начальное и конечное состояния x0 и xk известны. Тогда последовательность состояний описывается конеч• ным вектором x = (x0, x1, . . . , xK ). Однако это представление можно легко распространить на бесконечные последовательности.
Условная вероятность P (xk+1|x0, x1, . . . , xk) состояния xk+1 в момент времени k + 1 при условии, что известны все состояния вплоть до момента
k, зависит только от состояния xk в момент k:
P (xk+1|x0, x1, . . . , xk) = P (xk+1|xk).
Определим переход ξk как пару состояний (xk+1, xk). Пусть Ξ представ• ляет собой множество переходов (возможно изменяющееся во времени)
Ξ = {ξk = (xk+1, xk)|P (xk+1|xk) =6 0}
Понятно, что |Ξ| 6 M 2.
21
Замечание 9.1. Очевидно, что между последовательностями со• стояний x и последовательностями переходов ξ = (ξ0, ξ1, . . . , ξK−1) су• ществует взаимно однозначное соответствие.
Предполагается, что рассматриваемый процесс наблюдается в шуме без памяти, т. е. для последовательности z наблюдений zk верояность zk зависит только от перехода ξk в момент k
KY−1
P (z|x) = p(z|ξ) = P (zk|ξk).
k=0
В теории информации последовательность z называют выходным сигналом канала без памяти.
Марковский процесс |
Переходы |
Канал без памяти |
Наблюдения |
|
|
|
|||
ξ = (ξ0, . . . , ξk−1) |
z = (z0, . . . , zk−1) |
|||
|
|
В цифровой связи обычно рассматривается следующая модель. Зна• чения uk входной последовательности u = (u0, u1, . . .) выбираются неза• висимо, согласно некоторому распределению вероятностей P (uk) и могут принимать одно из m значений. Имеется ненаблюдаемая сигнальная по• следовательность y, в которой каждое yk определяется текущей uk и ν предыдущими значениями входных величин
yk = f (uk, uk−1, . . . , uk−ν ).
Наблюдаемая последовательность z представляет собой выходной сиг• нал канала без памяти, на вход которого поступает y. Такой процесс на• зывается процессом сдвигающего регистра (shift-registre process), так как его можно промоделировать с помощью сдвигающего регистра длины ν, на вход которого поступают uk. Аналогия этой модели с общим подходом становится понятной после введения определений состояния xk и перехода ξk. Положим
xk = (uk−1, uk−2, . . . , uk−ν ), |
ξk = (uk, uk−1, . . . , uk−ν ). |
Таким образом, число состояний |X| = mν , а число переходов |Ξ| = mν+1. Пусть входная последовательность ”начинается“ в момент времени 0 и ”за• канчивается“ в момент времени K − ν, т. е.
u = (. . . , 0, u0, u1, . . . , uK−ν , 0, 0, . . .).
Тогда процесс сдвигающего регистра фактически начинается в момент вре• мени 0 и заканчивается в момент времени K, причем x0 = xK = (0, 0, . . . , 0).
22
Сформулируем теперь задачу, решение которой дает АВ. Имеется по• следовательность z наблюдений дискретного марковского процесса с конеч• ным числом состояний, наблюдаемого в шуме без памяти. Требуется найти последовательность состояний x, для которой апостериорная вероятность P (x|z) максимальна. В силу замечания 9.1 нужно найти последователь• ность переходов ξ, для которой P (ξ|z) максимальна.
Для рассмотреной выше модели сдвигающего регистра это равносиль• но также отысканию наиболее вероятной входной последовательности u, поскольку между последовательностями u и x очевидно существует взаим• но однозначное соответствие. Если функция f выбрана так, что есть взаим• но однозначное соответствие между последовательностями y и x то можно говорить о поиске наиболее вероятной сигнальной последовательности y.
Замечание 9.2. Известно, что обсуждаемый принцип МАВ мини• мизирует вероятность ошибки при обнаружении полной последователь• ности (вероятность ошибки в блоке, сообщении или слове).
Описание алгоритма
Покажем, что сформулированная выше задача оценивания последова• тельности по критерию МАВ равносильна задаче отыскания кратчайшего пути в некотором графе.
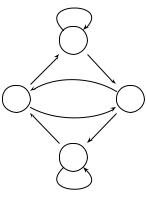
С дискретным марковским процессом с конеч• |
|
|
ным числом состояний связывают ориентированный |
|
00 |
граф, называемый диаграммой состояний. На рисун• |
|
|
|
|
|
ке справа приведен ориентированный граф диаграм• |
|
|
мы состояний процесса сдвигающего регистра с че• |
01 |
10 |
тырьмя состояниями. Вершины графа отображают |
|
|
состояния, а ребра возможные переходы. Для более |
|
11 |
подробного описания процессов используют ориенти• |
|
|
|
|
|
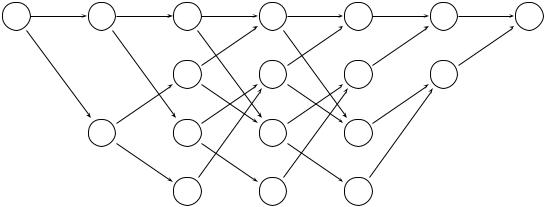
рованные графы, называемые решетчатой диаграм• |
|
|
мой состояний. В этом графе каждая вершина сооответствует отдельному состянию в данный момент времени, а каждое ребро отображает переход к некоторому новому состянию в следующий момент времени. Решетка на• чинается и заканчивается известными состояниями x0 и xK .
Важнейшим свойством решетчатой диаграммы является то, что каж• дой возможной последовательнсти состояний x соответствует единствен• ный ориентированный путь по графу, и наоборот.
23
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
|
01 |
01 |
01 |
01 |
|
|
10 |
10 |
10 |
10 |
|
|
11  11
11  11
11
Для заданной последовательности наблюдений z сопоставим каждому ориентированному пути в решетчатой диаграмме состояний некоторую дли• ну, пропорциональную − ln P (x, z), где x последовательность состояний, связанная с этим путем. Тогда можно найти последовательность состояний x , для которой P (x|z) максимальна, или (в силу определения условной ве• роятности) максимальна P (x, z) = P (x|z)P (z). Учитывая, что ln P (x, z) монотонная функция аргумента P (x, z) и между путями и последователь• ностями состояний существует взаимно однозначное соответствие путь ми• нимальной длины соответствует x . В силу свойств марковского процесса и отсутствия памяти для P (x, z) справедливо представление:
K−1 |
K−1 |
|
Y |
Y |
|
P (x, z) = P (x|z)P (z) = |
P (xk+1|xk) P (zk|xk+1, xk). |
(9.1) |
k=0 |
k=0 |
|
Припишем каждому ребру (переходу) длину
λ(ξk) = − ln P (xk+1|xk) − ln P (zk|ξk).
Тогда в силу (9.1) общая длина пути, соответствующая некоторой последо• вательности состояний x окажется равной
KX−1
λ(ξk) = − ln P (x, z),
k=0
как и утверждалось ранее.
Перейдем к задаче нахождения кратчайшего пути в ориентированном графе.
Обозначим через xk0 отрезок (x0, x1, . . . , xk) включающий состояния из последовательности состояний x вплоть до момента времени k. В решетке отрезок xk0 соответствует отрезку пути, начинающемуся в вершине x0 и заканчивающемся в вершине xk. Для произвольной вершины xk среди всех
24
таких путей, с длинами
Xk−1
λ(xk0 ) = λ(ξi)
i=0
выберем кратчайший. Такой путь будем называть уцелевшим отрезком, соответствующим вершине xk и обозначать xˆ(k). Очевидно, что в любой момент времени k > 0 существует не более M уцелевших отрезков. Легко показать, что кратчайший полный путь x должен проходить через один из уцелевших отрезков.
Таким образом, к моменту k + 1 нужно только продолжить все уце• левшие к моменту k отрезки на следующий момент времени, вычислить длины увеличенных отрезков пути и для каждой вершины xk+1 выбрать кратчайший, в качестве нового уцелевшего отрезка.
Замечание 9.3. В описанном алгоритме нетрудно увидеть простой вариант прямого динамического программироывания.
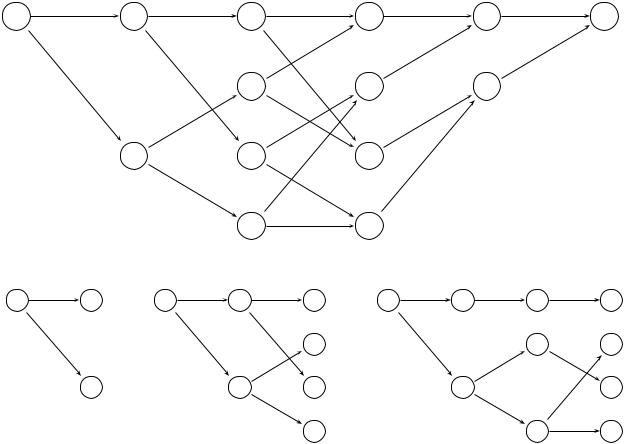
Поясним данный алгоритм на примере решетчатой диаграммы для четырех состояний, охватывающей пять единиц времени (M = 4, K = 5). На каждом ребре графа указана длина. (В практическом случае длины будут функциями принятых данных).
00 |
1 |
1 |
00 |
|
0 |
00 |
2 |
1 |
00 |
|
|
|
00 |
00 |
|||
|
|
|
|
2 |
|
0 |
1 |
|
|
1 |
1 |
01 |
|
2 |
01 |
01 |
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
0 |
|
1 |
|
|
|
|
|
1 |
1 |
|
1 |
|
|
10 |
|
10 |
|
10 |
|
||
|
|
|
|
|
|
|||
|
|
0 |
|
|
1 |
|
|
|
|
|
|
11 |
|
1 |
11 |
|
|
|
|
|
|
|
|
|
||
Получаем пять последовательных шагов
00 |
00 |
1 |
00 |
00 |
00 |
2 |
00 |
00 |
00 |
00 |
2 |
|
|
|
|
|
01 |
3 |
|
|
01 |
01 |
2 |
|
10 |
1 |
|
10 |
10 |
2 |
|
10 |
|
10 |
3 |
|
|
|
|
|
11 |
1 |
|
|
11 |
11 |
2 |
25

00 |
|
00 |
2 |
00 |
00 |
00 |
3 |
|
01 |
01 |
3 |
|
01 |
|
|
10 |
|
|
|
|
10 |
|
|
11 |
11 |
|
|
|
11 |
|
|
Приведем алгоритм в формальном виде. |
|
|
|||||
Иницализация: k = 0; |
|
xˆ(x0) = x0; |
|
(x0) = 0. |
|
|
|
Очередной шаг: Вычислить |
|
|
|
|
|
||
(xk+1, xk) = (xk) + λ[ξk = (xk+1, xk)]
для всех ξk = (xk+1, xk). Найти
(xk+1) = min (xk+1, xk)
xk
для каждого xk+1 и соответствующий уцелевший отрезок xˆ(xk+1). Перейти от k к k + 1 и повторять операции до k = K.
Замечание 9.4. Если последовательности состояний имеют очень большую длину, то уцелевшие отрезки необходимо усекать до приемли• мой для обработки длины δ. То есть к моменту k алгоритм должен дать определенное решениеотносительно вершин, соответствующих момен• там времени вплоть до k − δ. Заметим, что в приведенном примере все уцелевшие до k = 4 отрезки вплоть до момента k = 2 проходят через одни и те же вершины.
Вообще, если длина усечения δ достаточно велика с большой вероят• ностью все уцелевшие до момента k отрезки будут вплоть до момента k − δ проходить через одни и теже вершины, так что начальный от• резок пути плоть до момента k − δ известным и может быть взят в качестве решения. Потери за счет усечения в этом случае невелики.
10.Алгоритм Герцеля
Рассмотрим вопрос3 о вычислении только одной компоненты спектра X = FN (x). Зафиксируем k 0 : N − 1 и согласно (2.2) запишем
X(k) = j=0 x(j) ωN−kj = x(0) + j=1 x(j) cos |
2N |
j |
−i j=1 x(j) sin |
2N j . |
|
N −1 |
N −1 |
|
|
N −1 |
|
X |
X |
πk |
|
X |
πk |
3Впервые опубликовано в [1]
26
Обозначим α = 2πk/N, cj = cos(αj), sj = sin(αj),
|
N −1 |
N −1 |
|
|
X |
X |
|
|
A(k) = x(j) cj , B(k) = |
x(j) sj . |
|
|
j=1 |
j=1 |
|
Тогда |
X(k) = x(0) + A(k) − iB(k). |
|
|
|
(10.1) |
||
Отметим, что |
|
|
|
cj + cj−2 |
= cos(αj) + cos(α(j − 2)) = 2 cos(α(j − 1)) cos(α) = 2 cos(α)cj−1, |
||
sj + sj−2 |
= sin(αj) + sin(α(j − 2)) = 2 sin(α(j − 1)) cos(α) = 2 cos(α)sj−1. |
||
Это порождает рекуррентные соотношения, на которых основаны даль• нейшие преобразования:
c0 |
= 1, c1 = cos(α), cj = 2 cos(α)cj−1 − cj−2, j = 2, 3, . . . , |
(10.2) |
s0 |
= 0, s1 = sin(α), sj = 2 cos(α)sj−1 − sj−2, j = 2, 3, . . . . |
|
Для вычисления A(k) и B(k) построим рекреннтную последователь• ность {gj } исходя из условий
x(j) = gj − 2 cos(α)gj+1 + gj+2, j = N − 1, N − 2, . . . , |
(10.3) |
gN +1 = gN = 0. |
|
Такое построение возможно. Действительно, при j = N − 1 получаем gN −1 = x(N − 1). Величины gN −2, gN −3, . . . , g1 определяются последова• тельно по формуле
gj = x(j) + 2 cos(α)gj+1 − gj+2, j = N − 2, . . . , 1, |
(10.4) |
||
gN = 0, gN −1 = x(N − 1). |
|
|
|
Согласно (10.3) и (10.2) имеем |
|
|
|
N −1 |
N −1 |
|
|
X |
X |
|
|
A(k) = |
x(j) cj = (gj − 2 cos(α)gj+1 + gj+2) cj = |
|
|
j=1 |
j=1 |
|
|
N −1 |
N |
N +1 |
|
X |
X |
X |
|
= |
gj cj − 2 cos(α) gj cj−1 + |
gj cj−2 = |
|
j=1 |
j=2 |
j=3 |
|
|
N −1 |
|
|
|
X |
|
|
= g1c1 + g2c2 − 2 cos(α)g2c1 + |
gj (cj − 2 cos(α)cj−1 + cj−2) = |
||
j=3
= g1c1 + g2(c2 − 2 cos(α)c1) = g1c1 − g2c0 = g1cos(α) − g2.
27
Аналогично, с использованием (10.3) и (10.2) преобразуется выражение для
B(k):
N −1 |
N −1 |
X |
X |
B(k) = x(j) sj = |
(gj − 2 cos(α)gj+1 + gj+2) sj = |
j=1 |
j=1 |
=g1s1 + g2s2 − 2 cos(α)g2s1 = g1s1 + g2(s2 − 2 cos(α)s1) = g1s1 =
=g1 sin(α).
Теперь формула (10.1) принимает вид:
X k |
) = |
x |
(0) + |
g |
1 cos( |
α |
) − |
g |
2 |
− |
i g |
α |
) = |
x |
(0) − |
g |
2 + |
g ω−k. (10.5) |
( |
|
|
|
|
|
1 sin( |
|
|
1 N |
Вычисление X(k) при фиксированном k по формуле (10.5) называется ал• горитмом Герцеля.
Основным элементом алгоритма Герцеля является схема (10.4) постро• ения последовательности {gj }. На самом деле нам нужна не вся последова• тельность {gj }, а только два ее члена g2 и g1. Для их вычисления необхо• димо N − 2 вещественных умножений и 2(N − 2) вещественных сложений.
11.Рекуррентная последовательность ортогональных базисов
C помощюю алгоритма Герцеля можно вычислить весь спектр сигна• ла, однако это не лучший метод. Существуют более эффективные методы, которые называются быстрым преобразованием Фурье (БПФ). Алгорит• мов БПФ много, и они зависят от арифметических свойств длины периода N . Мы сосредоточимся на случае, когда N = 2s.
Рассматриваемый подход к БПФ связан с построением в пространстве сигналов рекррентной последовательности ортогональных базисов.
В пространстве CN построим рекррентную последовательность орто•
гональных базисов f0, f1, . . . , fs. Здесь fν = {fν (k; j)}Nk=0−1. Сигнал fν (k; j) как элемент пространства CN будем обозначать fν (k). Введем обозначения
Nν = N/2ν ,
Последовательность fν = {fν (k; j)}Nk=0−1, ν = 0, 1, . . . , s определим так:
|
f0(k) = δ(· − k), k 0 : N − 1; |
|
|
|||||||
f (l + p |
|
|
) = f |
ν−1 |
(l + 2p |
|
) + ωl |
f |
(l + (2p + 1)Δ ), |
|
ν |
ν |
+1 |
|
|
ν |
|
ν+1 ν−1 |
ν |
(11.1) |
|
fν (l + ν + p |
ν |
+1) = fν−1(l + 2p |
ν ) − ωl |
ν+1 fν−1(l + (2p + 1)Δν ), |
|
|||||
|
|
p 0 : Nν − 1, |
l 0 : |
ν − 1, |
ν = 1, 2, . . . , s. |
|
||||
28
Заметим, что ω |
ν+1 = ω2 = −1. Тогда, вводя параметр σ 0, 1 рекуррентные |
|||||||||
|
|
|
ν |
|
|
|
|
|
|
|
соотношения (11.1) можно записать одной строкой |
|
|||||||||
f (l + σ |
ν |
+ p |
ν+1 |
) = f |
ν−1 |
(l + 2p |
ν |
) + ωl+σ |
ν f |
(l + (2p + 1)Δ ) (11.2) |
ν |
|
|
|
ν+1 |
ν−1 |
ν |
||||
при тех же ограничениях на индексы p, l и ν, что и в соотношениях (11.1).
Пример 11.1. В частности, получаем
1) при ν = 1 для p 0 : N/2 − 1
f1(2p) = f0(2p) + f0(2p + 1), f1(2p + 1) = f0(2p) − f0(2p + 1),
2) при ν = 2 для p 0 : N/4 − 1
f2(4p) = f1(4p) + f1(4p + 2), f2(4p + 1) = f1(4p + 1) + if1(4p + 3), f2(4p + 2) = f1(4p) − f1(4p + 2), f2(4p + 3) = f1(4p + 1) − if1(4p + 3).
Заметим, что коэффициентами в (11.2) при правом слагаемом суммы являются последовательно все корни степени ν из единицы: {1, −1} для
ν = 1, {1, i, −1, −i} для ν = 2.
Что представляет собой последний базис fs? Для ответа на этот вопрос потребуется некоторая подготовка.
Введем перестановку rev ν . Она определена на множестве натуральных
чисел {0, 1, . . . , 2ν − 1} и сопоставляет числу j = (jν−1, jν−2, . . . , j0)2 число rev ν (j) = (j0, j1, . . . , jν−1)2, двоичный код которого равен перевернутому
двоичному коду числа j. Идентификатор rev связан с английским словом reverse. Индекс ν у rev ν определяет количество ревертируемых разрядов.
|
|
Ясно, что rev ν (rev ν (j)) = j при j 0 : ν − 1. Отсюда, в частности, |
|||||||||||||||
следует, |
что отображение j |
→ |
rev |
ν ( |
j |
) |
является перестановкой множества |
||||||||||
ν |
|
|
|
|
|
|
|
|
|
|
|||||||
{0, 1, . . . , 2 − 1}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Из определения следует, что rev 1(j) = j при j 0 : 1. В следующей |
|||||||||||||||
таблице показано, как формируется перестанока rev ν при ν = 3. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
j |
(j2, j1, j0)2 |
|
(j0, j1, j2)2 |
rev 3(j) |
|
|
|
j |
(j2, j1, j0)2 |
(j0, j1, j2)2 |
|
rev 3(j) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
(0, 0, 0)2 |
|
(0, 0, 0)2 |
|
0 |
|
|
|
|
4 |
(1, 0, 0)2 |
(0, 0, 1)2 |
|
1 |
|
|
|
1 |
(0, 0, 1)2 |
|
(1, 0, 0)2 |
|
4 |
|
|
|
|
5 |
(1, 0, 1)2 |
(1, 0, 1)2 |
|
5 |
|
|
|
2 |
(0, 1, 0)2 |
|
(0, 1, 0)2 |
|
2 |
|
|
|
|
6 |
(1, 1, 0)2 |
(0, 1, 1)2 |
|
3 |
|
|
|
3 |
(0, 1, 1)2 |
|
(1, 1, 0)2 |
|
6 |
|
|
|
|
7 |
(1, 1, 1)2 |
(1, 1, 1)2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|||

Будем считать, что rev 0(0) = 0.
Лемма 11.1. Справедливо следующее рекуррентное соотношение
rev ν (2q + σ) = σ ν + rev ν−1(q) |
(11.3) |
при σ 0 : 1, q 0 : ν − 1, ν = 1, 2, . . ..
Доказательство. При ν = 1 формула (11.3) принимает известный вид rev 1(σ) = σ. Пусть ν > 2. Возьмем q 0 : ν − 1. Имеем
q = qν−22ν−2 + · · · + q12 + q0, 2q + σ = qν−22ν−1 + · · · + q02 + σ, rev ν (2q + σ) = σ2ν−1 + q02ν−2 + · · · + qν−2 = σ2ν−1 + rev ν−1(q).
Соотношение (11.3) позволяет последовательно вычислять значения
rev ν (j) при ν = 1, 2, . . . сразу для всех j {0, 1, . . . , ν+1 −1}. При этом до• статочно вычислять rev ν (j) только для четных j так как из (11.3) очевидно
следует
rev ν (2q + 1) = rev ν (2q) + ν = rev ν (2q) + 2ν−1, q = 0, 1, . . . , ν − 1.
В следующей таблице показаны результаты вычисления rev 1(j), rev 2(j) и rev 3(j).
ν |
rev ν (j) при j = 0, 1, . . . , |
ν+1 − 1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
2 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
4 |
2 |
6 |
1 |
5 |
3 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
8 |
4 |
12 |
2 |
10 |
6 |
14 |
1 |
9 |
5 |
13 |
3 |
11 |
7 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 11.1. Из приведенной таблицы становится очевидным еще одно свойство перестановки rev ν (j)
rev ν (q + ν ) = rev ν (q) + 1, q 0 : ν − 1.
Вернемся к рекуррентным соотношениям (11.2).
Теорема 11.1. Справедлива формула
fν (l + p ν+1) = |
ωl rev ν (q) f0(q + p |
ν+1), |
(11.4) |
ν+1−1 |
ν+1 |
|
|
X
q=0
30
