№2

1. Дії над матрицями. Властивості дій над матрицями.

Знайти матрицю С=2А+3ВА, якщо

, .

2. Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння площини і його дослідження.

3. Диференціювання неявно заданих функцій.

Знайти похідну функції .

4. Похідна за напрямом вектора та градієнт функції.

Знайти градієнт функції Z=3x +y в точці М (-2;1), та його величину

5. Диференціальні рівняння першого порядку. Основні поняття.

№5

1. Квадратній матриці А n-го порядку можна поставити у відповідність число detА,яке називається визначником цієї матриці.Властивості визначника:

1.Визначник не змінюється ,якщо його рядки замінити відповідними стовпцями.

2.Якщо у визначнику поміняти місцями два рядки ,то визначник змінить свій знак на протилежний.

3.Якщо один з рядків (стовпців )визначника складається тільки з нулів ,то визначник дорівнює нулю.

4.якщо визначник має два однакових рядки(стовпці),то він дорівнює нулю.

5.Спільний множник ,який мають усі елементи деякого рядка (стовпця)визначника,можна винести за знак визначника.

6.Якщо у визначнику елементи двох рядків (стовпців)пропорційні, то визначник дорівнює нулю.

7.Визначник не змінюється ,якщо до елементів одного рядка (стовпця)додати відповідні елементи іншого рядка(стовпця),помножені на одне і теж число.

|2 3 1 | 2 3|

Det=|-1 5 1|-1 5|=20+12-3-20-6+6=9

|4 3 2 |4 3 |

2.Кут між двома прямими L₁ та L_2,заданими канонічними рівняннями , визначається кутом φ між непрямими векторами l1=(m,k,p) та l2(m2,k2,p2) цих прямих, а саме:

УМОВИ пар і пер прямої і площини

Умова паралельності прямої та площини

Am+Bn+Cp=0

Умова перпендикулярності прямої і площини: ║

- пряма 2x+z-11=0 - площина

n=(2,0,1) l=(-1,2,3)

sin = =

3. Головну лінійну відносно частину приросту функції називають диференціалом функції і позначають dy=f’(x)dx.

Властивості:

1. Диференціал сталої дорівнює 0 (dc=0)

2. Cталий множник можна виносити за знак диференціала: dcu=cdu

3. Диференціал суми дорівнює сумі диференціалів: d(u±v)=du±dv

4. Диференціал добутку дорівнюэ добутку диференціала першого множника на другий та добутку першого на диференціал другого: d(uv)=vdu+udv

5. Диференціал частки: = .

6. Диференціал складної функції : dy= .

y=ln5x/x^2 y`=( ln5x/x^2)` y`=

4. Розглянемо ф-цію z=f(x,y). Екстремум цієї ф-ції при умові, що змінні х, у пов’язані умовою φ(х,у)=0, називається умовним. Геометрично це означає, що точка М(х,у) лежить на лінії,визначеній рівнянням φ(х,у)=0. Дл знаходження умовного екстремуму можна діяти наступним чином.

Введему ф-цію Лагранжа F(x,y)=f(x,y)+λ φ(х,у) і запишемо систему

Розвязавши сит. рівнянь отримуємо критичні точки ф-ції F(X,y) Питання про існування екстремуму в критичних точках вирішується окремо,зокрема,з фіз.. або геометр. міркувань. Для ф-ції u=f(x,,y,z) з двома рівняннями зв’язку і ф-ція Лагранжа має вигляд F=f+λ1 φ1+ λ2 φ2, а сист. записується так:

Розвязавши сит. рівнянь отримуємо критичні точки ф-ції F(X,y) Питання про існування екстремуму в критичних точках вирішується окремо,зокрема,з фіз.. або геометр. міркувань. Для ф-ції u=f(x,,y,z) з двома рівняннями зв’язку і ф-ція Лагранжа має вигляд F=f+λ1 φ1+ λ2 φ2

(точно не знаю) z=4xy^2 за умови 2x+y=1 L(x,y,λ)= 4xy^2 +λ(2x+y-1)

y^2=λ/2 y= x=-λ/8y=-λ/8* λ=5/8

y=2/ λ=5/8

=0

5. Означення 8. Однорідним диференціальним рівнянням пер-шого порядку називають рівняння, яке можна звести до вигляду

у'' = f(x,l/) , (16)

де функція f(x,y) не змінюеться при заміні х ma у на tx ma ty, тобто задовольняе умову

f[tx,ty) = f[x,y).

Відмітимо, що функцію fyx,yj яка задовольняє вказану умову,

називають однорідною нульового виміру.

Однорідне диференціальне рівняння першого порядку шляхом підстановки

y y=uv y

y -x/y=1 y -1/x*y=1 -(1/x)uv=1

dv/dx=v/x dv/v=dx/x

Lnv=lnx v=x u=-1/x^2+C

Y=(-1/x^2+C)*x-загальний розв’язок

Білет 17

1. Ве́кторний (ліні́йний) про́стір — основне поняття лінійної алгебри, узагальнення множини всіх векторів на площині чи в просторі з операціями додавання векторів та множення вектора на скаляр.

Означення 8. Лінійно залежними називають вектори , якщо існує хоч би одне дійсне число (і = 1,2,…, n), що не дорівнює нулю і виконується рівність

Означення 9. Лінійно незалежними називають вектори , якщо рівність (7) виконується

тільки тоді, коли усі . В системі векторів a1,a2…an число лінійно незалежних векторів дорівнює рангу матриці, яка складена з координат цих векторів.

Дійсно, якщо систему векторів a1,a2…an із простору Еm розглядати як матриці-стовпці з m заданими елементами, тоді рівняння (1) можна записати у вигляді однорідної системи m лінійних алгебраїчних рівнянь з n невідомими . Кількість базисних невідомих системи дорівнює рангу r основної матриці системи, тобто матриці, складеної із координат векторів a1,a2…an .

Таким чином, серед чисел існує r не рівних нулю. Згідно з означенням звідси випливає, що вектори a1,a2…an лінійно залежні.

Для лінійно залежних векторів має місце рівність (1), з якої завжди можна один вектор виразити через лінійну комбінацію інших.

Якщо вектори a1,a2…an із простору Еn (кожен з них має n координат) лінійно незалежні, тоді , тобто система n однорідних лінійних алгебраїчних рівнянь з n невідомими має тривіальний розв’язок. Але це можливо тоді, коли визначник матриці, складеної із координат векторів a1,a2…an , не дорівнює нулю.

det= =8+1+45-10-6-6=32 det=0 вектори утворюють базис

2. Т1.Функція y=f(x) не може мати двох різних границь в одній точці.

Т2.Якщо в деякому околі точки х0,крім, можливо самої точки х0,виконується нерівність f(x)≤ῳ(x) і кожна з функцій f(x) і φ(x) та має границю в точці х0,то ≤

T3.Нехай в деякому околі точки х0,крім, можливо самої точки х0, то виконується нерівність φ(x)≤ f(x)≤ψ(х).Якщо функції φ(x) та ψ(х) мають границю в точці х0 при чому = =А то функція f(x) також має границю в цій точці і =А.

Т4.Якщо функція має в точці х0 границю тобто =А то y=f(x) – обмежена при х→х0.

=1/0=∞

3. Функція z одержить приріст Δхz = f (x+ Δx,y) – f (x; y), який називають частинним приростом по змінній х.

Якщо приросту надати змінній у, то функція z одержить приріст ΔуZ = f (x+ Δx,y) – - f(x; y), який називають частинним приростом по змінній у. Якщо існує границя lim ,що не залежить від способу прямування , то її називають частинноюпохіднопершого порядку функції : u = f ( , , ..., ) по змінній і позначають або або u´ .

z=2x*lny+3(x^2)*(y^3)+3^x

dz/dx=2*lny+6xy^3+

dz/dy=2x

4. Означення 1. Дріб називається раціональним, якщо його чи­сельник та знаменник є многочленами, тобто дріб має вигляд

де а_і та b_k — коефіцієнти многочленів, і = 0, 1, ..., n;

k = 0, 1, 2, ..., m.

Раціональний дріб називається правильним, якщо найвищий показник степеня чисельника n менше відповідного степеня m знаменника. Дріб називається неправильним, якщo .

Якщо дріб неправильний, тоді треба поділити чисельник на знаменник (за правилом ділення многочленів) і одержа­ти заданий дріб у вигляді суми многочлена та правильного ра­ціонального дробу, тобто

Означення 2. Найпростішими раціональними дробами І, II, III та IV типу називають правильні дроби вигляду:

I. II.

III.

IV.

Умова означає, що квадратний тричлен х² + px + q не має дійсних коренів і на множники не розкладається. Те саме можна сказати і про квадратний тричлен x² + rx + s.

Розглянемо інтегрування найпростіших раціональних дробів. Інтеграли від найпростіших раціональних дробів 1-го та ІІ-го типів знаходять методом безпосереднього інтегрування:

І.

ІІ.

При інтегруванні найпростішого дробу ІІІ-го типу треба спочат­ку в знаменнику виділити повний квадрат, а потім той вираз, що під квадратом, замінити через нову змінну.

ІІІ.

Повертаючись до змінної х, та враховуючи, що або одержимо:

Інтеграл від найпростішого дробу типу IV шляхом повторного інтегрування частинами зводять до інтеграла під найпростішого дробу типу III.

=4 = =4 =4* = +C

5. Перш ніж обчислювати суму ряду, треба переконатись в його збіжності. Інакше

можна витратити великі зусилля на пошук неіснуючої суми.

Теорема про необхідну ознаку збіжності ряду. Якщо ряд збіжний, то його

загальний член n a прямує до нуля при необмеженому зростанні n .

Доведення. Припустимо, що ряд 1 2 3 a + a + a +K є збіжним. Тоді для нього

справедлива рівність n n

lim S S

. Справедливою буде також і рівність n n 1

lim S S

оскільки, коли n®¥, то і (n -1)®¥ . Віднімемо від першої рівності другу:

n n n n 1

lim S lim S 0 ®¥ ®¥ -

- = або ( ) n n n 1

lim S S 0 ®¥ -

- = .

Робимо остаточний висновок: оскільки n n1 n S S a - - = , то n n

lim a 0

®¥

= .

Ознака порівняння. Нехай задано два знакододатні числові ряди:

та для всіх n виконується нерівність an <= bn . Тоді, якщо ряд (5) збіжний, то

збіжний і ряд (4). Якщо ряд (4) розбіжний, то розбіжний і ряд (5).

Порівняємо ряд =6/3+6/2*3^2+…+ … з еталонним рядом =6/3+6/3^2+…+ ,

, заданий ряд збігає

Білет №3

1. Визначники квадратних матриць. Способи обчислення визначників. Обчислити визначник двома способами:

Визначник – це число, що відповідає тільки квадратній матриці. Визначником другого порядку називають число, що дорівнює різниці добутків елементів головної та побічної діагоналей. Визначником третього порядку називають число, що обчислюється за правилами: Саррюса та трикутника. Визначником n-го порядку називають число, що дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпчика на відповідні їм алгебраїчні доповнення. Алгебраїчне доповнення – це мінор зі знаком . . Мінор - визначник, що залишився після викреслення і-го рядка та j-го стовпчика.

Визначник можна обчислити двома способами: Саррюса(шляхом дописання 2-х перших рядків до матриці) та трикутника.

2. Кут між площинами. Умови паралельності і перпендикулярності двох площин.

Знайти кут між площинами та .

3. Похідна степенево – показникових функцій.

Знайти похідну функції .

4. Обчислення наближеного значення функції в точці за допомогою повного диференціала.

Обчисліть за допомогою повного диференціала (1,04) (0,01) .

5. Диференціальні рівняння з відокремлюваннями змінними.

Знайти загальний розв’язок рівняння .

Білет №16

1.Мішаний добуток, властивості мішаного добутку.

Знайти об’єм піраміди побудованої на векторних , якщо . 39

2.Еквівалентні нескінченно малі величини. Ланцюжок еквівалентних нескінченно малих величин (при х → 0 і при х → х₀ ).

Обчислити границю: . 91

2.Лінії рівня функції двох змінних.

Побудувати лінії рівня функції . 154

2. Інтегрування тригонометричних функцій.

Знайти . 189

2. Узагальнений гармонічний ряд та ряд геометричної прогресії.

Дослідити збіжність ряду . 242

№23 23

1. Рівняння прямої з кутовим коефіцієнтом.

Записати рівняння прямої з кутовим коефіцієнтом, якщо , .

2. Властивості функцій, неперервних на відрізку. Дослідити на неперервність функцію на відрізку .

3. Алгоритм дослідження функції на екстремум за допомогою першої похідної .

Знайти екстремум функції .

4. Метод інтегрування заміни змінної у визначеному інтегралі.

Знайти визначений інтеграл 5. Абсолютна та умовна збіжність рядів.

Дослідити збіжність

1. Рівняння прямої з кутовим коефіцієнтом.

Кутовим коефіцієнтом прямої називається тангенс кута нахилу прямої до осі Ox , який відраховується в додатному напрямі (від осі до прямої проти годинникової стрілки). Цей кут завжди розглядається в межах від нуля до , тобто .

Рівняння прямої з кутовим коефіцієнтом має вигляд y = k * x + b , де k = tg – кутовий коефіцієнт, b – початкова ордината, тобто точка перетину прямої з віссю Oy

2. Властивості функцій, неперервних на відрізку

Якщо функція неперервна в кожній точці інтервалу (а,b), то вона називається неперервною на цьому інтервалі.

Функція неперервна на відрізку [а,b], якщо вона неперервна на (а,b) і, крім того, неперервна справа в точці а і зліва в точці b.

Сформулюємо теореми про неперервні функції.

Теорема 1 (перша теорема Больцано-Коші). Якщо функція y = f (x)

неперервна на відрізку [а; b] і на його кінцях набирає значень різних знаків, то всередині відрізка [а; b] знайдеться хоча б одна точка x = c , в якій функція дорівнює нулю.

Теорема 2 (друга теорема Больцано-Коші). Нехай функція y = f (x)

неперервна на відрізку [а; b] і набуває на його кінцях різних значень: f (a) 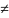f (b) . Тоді для довільного числа [ f (a); f (b)] знайдеться таке число c (a; b) , що f (c) .

Теорема 3 (Вейєрштрасса). Якщо функція y = f (x) неперервна на відрізку [а; b], то серед її значень на цьому відрізку існує найбільше і найменше.

3. Алгоритм дослідження функції на екстремум.

Максимум та мінімум функції кількох змінних називають екстремумами функції, а точку , де ф-ція має екстремум називають точкою екстремуму ф-ції.

Алгоритм.

1. Знайти область визначення функції.

2. Знайти частинні похідні I-го порядку 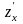та .

3. Розв’язати систему та знайти критичні точки.

4.За достатніми ознаками зробити висновок про екстремум.

5. Знайти значення функції в точках екстремуму.

4. Метод інтегрування заміни змінної у визначеному інтегралі.

Якщо функція f(x) неперервна на відрізку -функція неперервна зі своєю похідною першого порядку на відрізку[ ], причому

для , то

Формулу називають формулою заміни змінної для визначеного

інтеграла.

Із сказаного випливає, що функція x = (t) на відрізку повинна бути

монотонною або іншими словами всі значення функції (t) повинні знаходитися на відрізку [a;b].

Абсолютна та умовна збіжність рядів.

Знакозмінний ряд

(1)

називається абсолютно збіжним, якщо збігається знакододатний ряд

(2)

складений з абсолютних величин його членів. Якщо ряд (1) збіжний, а ряд (2) розбіжний, то ряд (1) називають умовно (не абсолютно) збіжним.

№26

1. Дії над матрицями. Властивості дій над матрицями. Знайти матрицю.

2. Означення похідної. Диференційовність та неперервність функції в точці і на проміжку.

Знайти похідну функції:

3. Правило Лопіталя.

Знайти границю, використавши правило Лопіталя .

4. Невласний інтеграл з нескінченною верхнею межею.

Знайти інтеграл .

5. Радіус, інтервал, область збіжності ряду.

№27

1. Визначники квадратних матриць. Способи обчислення визначників.

Обчислити визначник двома способами:.

2. Правила диференціювання сталої, суми, добутку, частки функцій, та наслідки з них.

Знайти похідну функції .

3. Екстремум функції, необхідна та достатня умови існування екстремуму.

Знайти екстремум функції .

4. Невласний інтеграл з нескінченною нижньою межею.

Знайти інтеграл

5. Ряд Тейлора.

Розкласти функцію за степенями

РОЗВЯЗОК

№28

1. Визначник -го порядку. Теорема Лапласа.

Квадратній матриці А n-го порядку можна поставити у відповідність число detА,яке називається визначником цієї матриці. Правило Лапласа:Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця )помноженні на відповідні алгебраїчні доповнення. Алгебраїчні доповнення Аij елемента aij

називають мінор цього елемента ,взятий із знаком «плюс»,якщо сума номерів рядка і стовпчика –число парне ,та зі знаком «мінус»,якщо непарне.Мінором Мij елемента aij визначника n-го порядку називається визначник ( n-1)-го порядку,який одержимо з даного визначника шляхом викреслювання і-го рядка та j-го стовпця,на пнрнтині яких знаходиться елемент aij.

Обчислити визначник використовуючи теорему Лапласа:

2. Похідна сталої та функцій (доведення). Таблиця похідних.

Знайти похідну функ

2. Частинний приріст і частинні похідні першого порядку.

Знайти частинні похідні першого порядку функції .

2. Відмінність між невласними інтегралами І та ІІ роду.7

Знайти інтеграл

2. Ряд Маклорена.

№7

1. Обернена матриця. Алгоритм оберненої матриці.

Оберненою для заданої квадратної матриці А називається така матриця , добуток якої на матрицю А як зліва, так і справа дорівнює одиничній матриці, тобто А , де Е – одинична матриця такого порядку, що і матриця А. Матриця має той же розмір, що й матриця А.

Будь-яка матриця, визначник якої не дорівнює 0, має обернену.

Щоб знайти обернену матрицю до даної потрібно:

1. Знайти визначник даної матриці А, det A . Якщо det А=0, то матриця особлива, і до неї оберненої не існує.

2. Знайти алгебраїчні доповнення елементів матриці А.

3. Скласти приєднану матрицю .

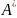4. Знайти обернену матрицю за формулою

.

5. Якщо потрібно, то зробити перевірку, використовуючи означення

Знайти матрицю обернену до даної матриці А.

1. Знаходимо визначник матриці А:

det A = 3*(-2)-1*2 = -8.

2. Знаходимо алгебраїчні доповнення:

= 2.

= -1.

= -2.

= 3.

3. Складаємо приєднану матрицю:

А =

4. Обернена матриця = =

   

5. Перевірка:

= Е.

2. Еліпс: означення, рівняння, графік,

Еліпсом називається геометричне місце точок площини, для кожної із яких сума віддалей до двох заданих точок, що називаються фокусами, є величина стала.

Якщо позначити через F₁ і F₂ точки, що є фокусами еліпса, а через

М — будь-яку точку, що належить еліпсу, то еліпс характеризується тим,

Рис 1

що

|MF₁| + |MF₂| = const.

Введемо Декартові системи координат так, щоб фокуси F₁ ,F₂ були розташовані на осі Ох, симетрично відносно початку координат (рис. 1). І нехай М(х, у) — будь-яка (біжуча) точка, що належить еліпсу. Віддаль |F₁F₂| позначимо через 2с: |F₁F₂| = 2с, а через 2а — сталу, про яку йде мова в означенні, тобто

|MF₁| + |MF₂| =2a

Очевидно, що для існування еліпса повинно бути 2а > 2с, або а>с. Фокуси еліпса матимуть координати F₁(—с, 0), F₂(c, 0). відстані

між двома точками дорівнюють

де b²=a²-c² (3)

яке називається канонічним рівнянням еліпса.

1.     Знайдемо розташування кривої відносно координатних осей. Із (3) дістаємо

звідки |x| ≤ aбо x

звідки |y| ≤ b або y

2.Еліпс розташований симетрично відносно координатних осей, тобто, якщо координати точки М₁(х,у) задовольняють рівняння (3), то його задовольняють і координати точок М₂(—х, у), М₃ (—х, —у),

M₄(x, —у). Отже, еліпс має дві осі симетрії, розташовані на координатних осях. Точка перетину осей симетрії є центром симетрії і називається центром еліпса. Для еліпса, зображеного рівнянням (3), центром є початок координат О(0, 0).

1.     Знайдемо точки перетину еліпса з координатними осями. Із (3) дістанемо: якщо х = 0, то у =± b, якщо y = 0, то х =± а. Отже, еліпс перетинає вісь Ох в точках А₁(—а, 0), А₂ (а, 0), а вісь Оу в точках В₁ (0, —b), B₂(0, b).

 

Рис 2

Точки А₁, А₂, B₁, В₂ перетину еліпса з його осями симетрії називаються вершинами еліпса (рис. 2). Відрізки А₁А₂ і B₁B розташовані на осях симетрії. Вони називаються осями еліпса. Відрізок А₁А₂, довжина якого 2а — велика вісь, а В₁В₂ — довжина якого 2b — мала вісь (а> b). Відповідно числа а та b називаються великою і малою півосями еліпса.

4. Фокальною хордою еліпса називається хорда, що проходить через фокус перпендикулярно до його великої осі. Довжина фокальної хорди позначається через 2р. Знайдемо число р — фокальну пів хорду. Якщо Н₁Н₂ (рис. 2) фокальна хорда, то точки Н₁ і Н₂ лежать на еліпсі і їх координати задовольняють рівняння (3). Тому для точки Н₂ (с, р) маємо

тобто

 

Отже, дістаємо

Числа а, b,с,р є параметрами еліпса.

1.     Ексцентриситетом еліпса називається число ε, що дорівнює відношенню фокальної півосі до великої півосі еліпса, і

(4)

оскільки с<а.

Величина ексцентриситету характеризує форму еліпса, його витягнутість по відношенню до осей. Перетворимо (4). Маємо

Звідси випливає, що якщо а = b, то ε = 0, і еліпс перетворюється на коло. Якщо b значно менше, ніж а, то число ε близьке до 1 і еліпс витягнутий вздовж осі Ох.

Аналогічно дістаємо, що |MF₁| = а + εх.

Тоді

|MF₁| + |MF₂|=2a.

Отже, рівняння (1) і (3) еквівалентні.

2. Правило Лопіталя.

Пра́вило Лопіта́ля —— метод знаходження границь функції, розкриття невизначеностей вигляду і . Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функції дорівнює границі частки їхніх похідних.

Правило говорить, що якщо функції і задовольняють такі умови:

1. або ;

2. ;

3. в проколотому околі ;

4. Якщо g(x) і f(x)— диференційовані в проколотому околі ,

то існує . При цьому теорема вірна і для інших баз (для вказаної буде наведено доказ).

Знайти границю за правилом Лопіталя

4. Невизначений інтеграл, основні властивості.

де F - первісна функції f (на проміжку); C - довільна стала.      Основні властивості.

     1.    

     2.    

     3. Якщо то

     4.

Знайти невизначений інтеграл для заданої функції f(x)=2x + – e

5. Диференціальні рівняння другого порядку, що дозволяють знизити порядок.

_Знайти загальний розв’язок рівняння

№14

Теорыя::::!!!!!!!!

1.

Розвязком СЛАР називається n значення невідомих х1=С1, х2=С2, х3=С3… хn=Сn при підстановці яких всі рівняння системи перетворюються в правильні рівності.

Система рівнянь називається сумісною,якщо вона має хоча б один розв*язок,і несумісною,якщо вона не має жодного розвязку.

Сумісна система називається визначеною,якщо вона має лише один розвязок,і невизначеною,якщо вона має безліч розв’язків.

Тут m - кількість рівнянь, а n - кількість невідомих. x1, x2, ..., xn - невідомі, які треба визначити. a11, a12, ..., amn - коефіцієнти системи - і b1, b2, ... bm - вільні члени -передбачаються відомими. Індекси коефіцієнтів (aij) системи позначаютьномери рівняння (i) та невідомого (j), при якому стоїть цей коефіцієнт, відповідно. Система (1) називається однорідною, якщо всі її вільні члени 

дорівнюють нулю (b1= b2 = ... = bm = 0), інакше - неоднорідною. Система (1) називається квадратною, якщо число m рівнянь дорівнює числу n-невідомих. Рішення системи (1) - сукупність n чисел c1, c2, ..., cn, таких, що підстановка кожного ci замість xi в систему (1) звертає всі її рівняння в тотожності. Система (1) називається сумісною, якщо вона має хоча б одне рішення, і несумісною, якщо у неї немає ніодного рішення. Сумісна система виду (1) може мати одне або більше рішень. Рішення c1 (1), c2 (1), ..., cn (1) і c1 (2), c2 (2), ..., cn (2) сумісної системи виду (1) називаються різними, якщо порушується хоча б одна з рівностей :

c₁⁽¹⁾ = c₁⁽²⁾, c₂⁽¹⁾ = c₂⁽²⁾, …, c_n⁽¹⁾ = c_n⁽²⁾.

Сумісна система виду (1) називається визначеною, якщо вона має єдине рішення, якщо ж у неї є хоча б два різних рішення, то вона називається невизначеною. Якщорівнянь більше, ніж невідомих, вона називається перевизначенною.

Однорідна система лінійних рівнянь AX = 0 завжди сумісна. Вона має нетривіальні(ненульові) рішення, якщо r = rank A <n.       Для однорідних систем базисні змінні (коефіцієнти при яких утворюють базисниймінор) виражаються через вільні змінні співвідношеннями види:

     Тоді n - r лінійно незалежними вектор-рішеннями будуть:

а будь-яке інше рішення є їх лінійною комбінацією. Вектор-рішення  утворюють нормовану фундаментальну систему.

     У лінійному просторі   безліч рішень однорідної системи лінійних рівнянь утворює підпростір розмірності n - r;   - базис цього підпростору.

2.

(нескінченно велика функція). Функція називається нескінченно великою при x ® aабо в точці a, якщо для будь-якого позитивного числа e знайдеться таке позитивнеd (e), що для всіх x № a і задовольняють умові | xa | <d буде виконано нерівність | f(x) | > e. Аналогічно можна дати визначення нескінченно великою при

  . Наведемо його у символічному запису:

lim_xf(x) = >0 ()>0  x:|x|> |f(x)|>.

3.

Функції декількох змінних Визначення. Якщо кожній парі (x, y) значень двох незалежних змінних з області Wставиться певне значення z, то говорять, що z є функція двох змінних (x, y). z = f (x, y) Геометричне зображення функції двох змінних - поверхню. Приватне і повний приріст функції. Повний приріст функції Dz = f (x + Dx, y + Dy)-f (x, y) Приватне приріст функції Dx z = f (x + Dx)-f (x, y) Dy z = f (x, y + Dy)-f (x, y) Взагалі, повний приріст функції не дорівнює сумі приватних збільшень. Приклад. z = xy. Dx z = (x + Dx) y-xy = yDx Dy z = x (y + Dy)-xy = xDy Dz = (x + Dx) (y + Dy)-xy = yDx + xDy + DyDx № Dy z + Dx z. Безперервність функції декількох змінних Межа функції. Нехай z = f (x, y) визначена в деякій околиці A (x0, y0). Визначення. Постійне число b називають межею z = f (x, y) при P (x, y) прагне до A,якщо для будь-якого e> 0 можна вказати таке значення d> 0, що для всіх x, що задовольняють нерівності | AP | <d , має місце нерівність | f (x, y)-b | <e. безперервна функція приватні похідні

4 . Метод невизначених коефіцієнтів.

Будь-який неправильний раціональний дріь розкласти на суму найпростіших раціональних дробів типу 1-4, коефіцієнти яких можна знайти за допомогою методу невизначених коефіцієнтів. Інтегрування дробів методом невизначених коефіцієнтів проводиться за такою послідовністю:

1)Перетворити даний драб у правильний.

2)Перетворити знаменник у добуток найпростіших могочленів.

3)Записати правилиний дріб у вигляді суми найпростіших дробів 1-4 типів, де в чисельнику стоять невизначені коефіцієнти.

4)Звести суму найпростіших дробів до спільного знаменника і отримати СЛАР, прирівнявши коефіцієнти при однакових степенях змінної..

5)Розвязок СЛАР дає невизначені коефіцієнти.

6)Кінцевий результат отримаємо післ обчислення інтегралів від многочлена і найпростіших дробів.

5. Властивості збіжних рядів.

Якщо ряд (∞∑n=1) a_n збігається і має суму S, то ряд (∞∑n=1)C∙ a_n, одержаний множенням даного ряду на число C, також збігається і має суму C∙S.

Якщо (∞∑n=1) a_n і (∞∑n=1) b_n -два збіжних ряди відповідно з сумами S₁ та S₂, то ряд (∞∑n=1) (a_n + b_n ) також збігається і його сума дорівнює S₁ + S₂.

Відкидання (приписування) скінченої кількості членів не впливає на збіжність ряду.

Для того, щоб ряд (∞∑n=1) a_n збігався, необхідно і достатньо, щоб залишок ряду R_n прямував до нуля при n→∞, тобто lim(n→∞)R_n=0.

№15 Теория!!!!!!!!!!!!!!!!!!!!!!!!!!!!