Задача нелинейного математического программирования (знмп)

100% - полезность денег гражданина Петрова

F(x)=(0,6)^tlnx

X₁ – короткий депозит на 1 год под 8% годовых

X₂ – длинный депозит на 2 года под 11% годовых

U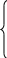 (x)=ln(100-X₁-X₂)+0,6*ln1,08*X₁+0,36Ln1,23X₂max

X₁+X₂=<100

X₁>=0

X₂>=0

Предприятие производит 2 вида продукции и использует при этом 3 вида ресурсов. Известны запасы ресурса на плановый период, нормативные величины затрат на продукцию и нормативные величины себестоимости единицы продукции.

Ресурс	Запас ресурса	Нормативы затрат на одно изделие
		А	Б
1	B1	A11	A12
2	B2	A21	A22
3	B3	A31	A32
Нормативная себестоимость		P1	P2

Значение величины a_ij и p_j были определены при условии, что при производстве продукции отсутствует брак. В реальных условиях наличие брака приводит к тому, что затраты сырья на единицу продукции a_ij

а_ij^Ф= а_ij+k_j*X_j

Себестоимость при этом также возрастает и зависит от объемов выпускаемой продукции

p_j^Ф=p_j+S_j*X_j

k_j; S_j – некоторые известные константы

x_j – продукции 1 и 2 вида

необходимо составить математическую модель для определения величин X_j при которых себестоимость всей выпущенной продукции является минимальной.

F (x)=(p₁+S₁X₁)X₁+(p₂+S₂X₂)X₂ min

(a₁₁+K₁X₁)X₁+(a₁₂+K₂X₂)X₂=<B1

(a₂₁+K₁X₁)X₁+(a₂₂+K₂X₂)X₂=<B2

(a₃₁+K₁X₁)X₁+(a₃₂+K₃X₂)X₂=<B3

F (x)=p₁x₁+S₁X²₁+p₂x₂+s2x₂²min

A₁₁X₁+k₁X²₁+A₁₂X₂+K₂X²₂=<B1

A₂₁X₁+k₁X²₁+A₂₂X₂+K₂X²₂=<B2

A₃₁X₁+k₁X²₁+A₃₂X₂+K₂X²₂=<B3

Задачи в которых целевая функция и/или система ограничений не являются линейными функциями от переменных задачи принято называть ЗНМП

Для решения ЗНМП используются два основных метода

1. Метод неопределенных множителей Лагранжа

Используется в двух случаях

1. Все ограничения системы ограничений имеют вид равенств

F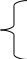 (x₁…x_n)max

ϕ₁(x₁….x_n)=b₁

….

ϕ _m(x₁….x_n)=b_m

ϕ ₁…. ϕ _m – скалярные функции от переменных задачи известного вида

с использованием функции ϕ и f составляется вспомогательная функция Лагранжа

L(X₁….X_n; λ₁….. λ_n)= f(x₁….x_n)+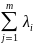 *[ϕ_i(x₁…x_n)-b_m]

Н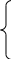 еобходимые условия максимум целевой функции f(x) записываются в виде системы нелинейных уравнений

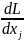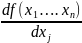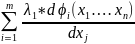= + =0

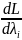=(ϕ_i(x₁…x_n)-b_i=0 i=1…m

ϕ ₁(x₁….x_n)=<b₁

….

ϕ _m(x₁….x_n)=<b_m

В классической постановке требуется чтобы все ограничения имели знак =<

Система ограничений неравенств путем введения дополнительных неотрицательных переменных приводится к виду ограничения равенств

При использовании этого метода основной проблемой является разрешимой полученной системы нелинейных уравнений

ϕ₁(x₁…x_n)+u²₁=b1

…..

Φ_m(x₁…x_n)+u²₁=b1

Необходимым условием максимума целевой функции f(x) определяются в результате решения системы нелинейных уравнений следующего вида

L (X₁….X_n; λ₁….. λ_n; u₁……u_m)= f(x₁….x_n)+ *[ϕ_i(x₁…x_n)+u_i²-b₁]

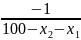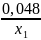= + = + +λ₁+ λ₂=0

=ϕ_i(x₁…x_n)-u_i²-b₁=0

=2λ_i*u_i=λ_i[b_i-ϕ_i(x₁….x_n)]=0

Полезность денег гражданина Петрова

U (x)=ln(100-X₁-X₂)+0,6*ln1,08*X₁+0,36Ln1,23X₂max

X₁+X₂=<100

X₁>=0

X

₂>=0

X₁+X₂=<100

-X₁=<0

-X₂=<0

X ₁+X₂+U²₂=<100

-X₁+ U²₂=<0

-X₂+ U²₃=<0

Данная система уравнений имеет имя: Условия Куна-Таккера

= + = + +λ₁+ λ₂=0

=ϕ_i(x₁…x_n)-u_i²-b₁=0

=2λ_i*u_i=λ_i[b_i-ϕ_i(x₁….x_n)]=0

2. Некоторый ограничения системы ограничений имеют вид неравенств

2. Градиентный метод