Задачи параметрического программирования (зпп)

ЗПП является обобщением задач ЗДЛП. В задачах ПП коэффициенты при переменных в целевых функциях зависят от некоторого параметра. Для задач параметрического программирования должны выполняться следующие условия

1. Коэффициенты целевой функции являются линейной функцией от некоторого параметра T

2. Система ограничения в задачи линейная и однозначно определяет выпуклый многогранник планов

3. Коэффициенты системы ограничений являются постоянными величинами

Целевая функция имеет вид

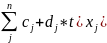
F (x) =  max

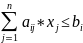
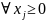
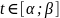
Для корректной постановки ЗПП необходимо задать интервал изменения параметра Т.

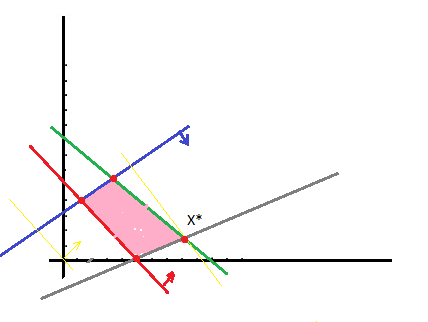
Геометрическая интерпретация ЗПП

Будем считать что число переменных =2, тогда целевая функция будет иметь вид t(x)=(c₁+d₁t)x₁+(c₂+d₂t)x₂

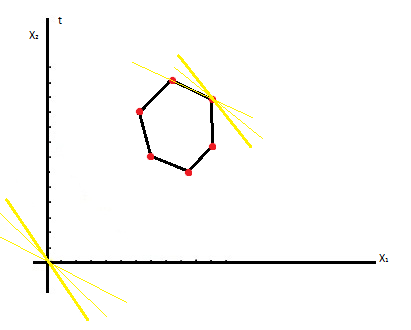
Таким образом исходя из характера поведения целевой функции можно окончательно определить основную цель решения ЗПП:

На заданном интервале изменения параметра Т, принадлежащего от α до β выделить под-интервалы от α1 до α2, от α2 до α3, от α3 до α4, в которых максимум целевой функции обеспечивается в одной и той же крайней точке многогранника плана, а также найти решение соответствующего каждому из под-интервалов.

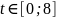
F(x)=4x1+(2+t)x2 max

2 x₁-5x₂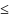 10

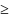X₁+X₅ 5

-x₁+x₂ 4

4x₁+5x₂ 40

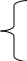
2x₁-5x₂=10

4x₁+5x₂=40

6x₁=50

X^*₁=8,33

X^*₂=1,33

X*=(8,33;1,33)

F(X*)=35,98

k_цф=-4/(2+t)

dk/dt=-1*(-4)/(2+t)²=4/(2+t)²

В нашем случае прямая будет вращаться против часовой стрелки.

В определенный момент k станет равен одному из ограничений (четвертому).

4/(2+t)=-4/5

П ри t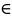 [0;3) Х*=(8,33;1,33)

-x₁+x₂ 4

4x₁+5x₂ 40

9х₂=56

Х^*₂=6,22

Х^*₁=2,22

При t (3;8] Х*=(2,22;6,22)

При t=3 Х*=[a;b]

Общие случаи решения зпп

Когда число переменных в задаче более 2, она не может быть решена графическим способом и для её решения используется модифицированный симплекс алгоритм.

Процедура реализуется в 2 этапа

1. Параметру t придают некоторое фиксированное значение t=α. Задачу приводят к классической ЗЛП. Решают ЗЛП

2. Определяют интервалы распределения параметра t в которых решение достигается в одной и той же точке многогранника решений.

Пусть этот интервал будет [α₁; α₂]

Указанный интервал сравниваю с интервалом [α;β] и исключают из рассмотрения/

3. Параметру t придают значение α₂ и повторяют этап 2

Порядок выделения под-интервалов

Придадим параметру t значение α и запишем задачу в виде симплекс таблицы.

В.П	С.Ч	Х1	Хr	Xn
Xn+1	B1	aij
Xn+k	Bk
Xb+	Bm
f α	0	-(c1+d1 α)	-(cr+dr α)	-(cn+dn α)
	0	-c1	-cr	-cn
	0	-d1	-dr	-dn

Предположим что мы все решили

В.П	С.Ч	Х1	Хr	Xn
X*n+1	B*1	α*ij
X*n+k	B*k
X*n+m	B*m
f α	F	-(p1+q1 α)	-(pr+qr α)	-(pn+qn α)
	P	-p1	-pr	-pn
	Q	-q1	-qr	-qn

Pj+qjα>=0

Таким образом для определения возможной границы изменения параметра t необоходимо проанализировать поведение величин

P₁+q₁t

P₂+q₂t

….

P_n+q_nt

Возможны 3 случая

1. Все qj>0. Верхней границы для t не существует, а нижняя определяется αj=max(-pi/qi) α2=+бесконечность

2. Все qj<0. Нижней границы для t не существует, α1=-бесконечность, α2=min(-pi/qi)

3. Среди qj есть положительные и отрицательные. Для t существуют обе границы. причем α k=max(-pi/qi) для всех qj>0 и α2=min(-pi/qi) для всех qj<0