Детерминистский случай. Метод Беллмана

Основная схема и главная идея метода динамического программирования (метода Беллмана) применительно к рассматриваемой проблематике достаточно проста и естественна. Рассмотрим конкретный пример де­терминистского дерева решений (рис. 4.4).

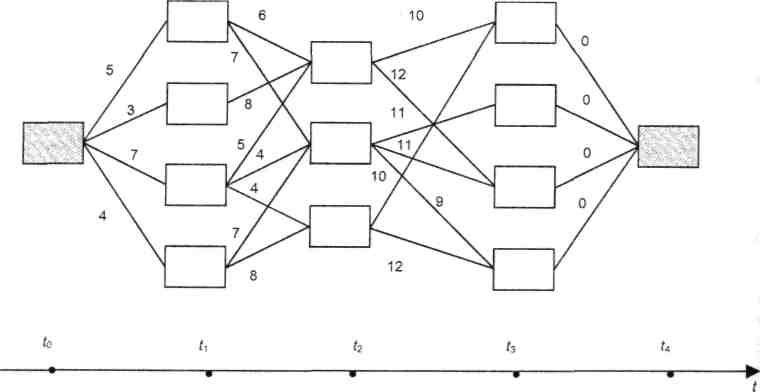
Рис. 4.4. Дерево решений с заданными локальными затратами

На рис. 4.4 одна начальная и одна конечная вершина. Легко видеть, что, по существу, конечными являются, все четыре вершины, соответствую­щие моменту времени . Однако с помощью введения фиктивной верши­ны для удалось свести задачу к графу с одной конечной вершиной. Точно так же можно поступать и с начальными вершинами, если их несколько. Числа у дуг графа означают трудоемкости (затраты), обеспечивающие переход от одной "решающей" вершины к другой. Дуги на промежутке имеют нулевые веса, что и означает, что все вершины отвечающие , являются, по существу, конечными. Главная задача заключается в выборе оптимального в смысле суммарных затрат пути, соединяющего начальную и конечную вершины.

Основная вычислительная идея метода Беллмана базируется на двух положениях:

• Задача поиска оптимального пути начинает решаться с конца.

• Исходная задача погружается в множество аналогичных задач с различными начальными вершинами и одной и той же конечной вершиной. При этом предполагается, что в качестве начальной вершины последовательно выступают все без исключения вершины графа.

Реализуем метод Беллмана для приведенного примера. Будем продвигаться по графу справа налево, выставляя определенные числа внутри каждой из вершин (помечая вершины) и указывая оптимальные направления движения из каждой вершины с помощью одной или нескольких стрелок. При этом числа внутри квадратиков-вершин будут означать всегда одно и то же — это суммарные затраты, которые получаются при движении из данной вершины, выбранной в качестве начальной, по оптимальному пути (т. е. это наименьшие из возможных затрат). Например, если мы имеем ситуацию, изображенную на рис. 4.5, а, где вершины 2,3,4 уже помечены, и надо пометить вершину 1, то будем рассуждать следующим образом (все вершины на рис. 4.5 для удобства объяснения пронумерованы в правом верхнем углу).

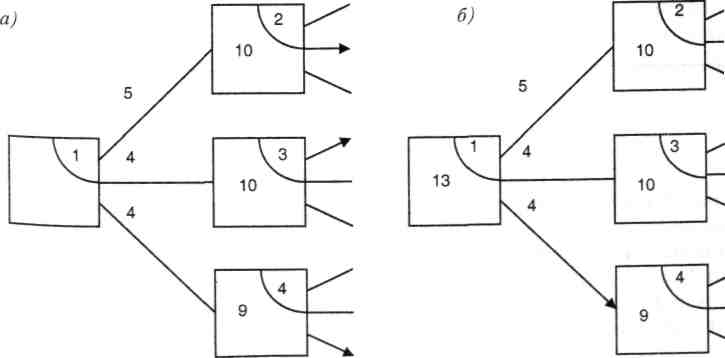
Рис. 4.5. Метод динамического программирования Беллмана

Если в качестве начальной взять вершину 1, то поиск оптимального пути из нее сводится к сравнению трех чисел: 5+10=15, 4+10=14, 4 + 9= 13. Наименьшее из этих чисел – 13, и, следовательно, именно число 13 мы запишем в вершине 1, а стрелочкой соединим вершины 1 и 4 (рис. 4.5, б). Действительно, по построению число 9 (полученное на пре­дыдущем этапе) означает минимальные возможные потери при движении из вершины 4 в фиксированную конечную вершину. Затраты в 4 единицы необходимы для перехода из вершины 1 в вершину 4. В итоге мы и получаем число 13. В двух других возможных случаях мы имеем большие затраты и, следовательно, оптимальный маршрут из вершины 1 лежит через вершину 4.

Продвигаясь справа налево, мы, обрабатывая последовательно верти­кальные слои вершин, разметим весь граф (рис. 4.6).

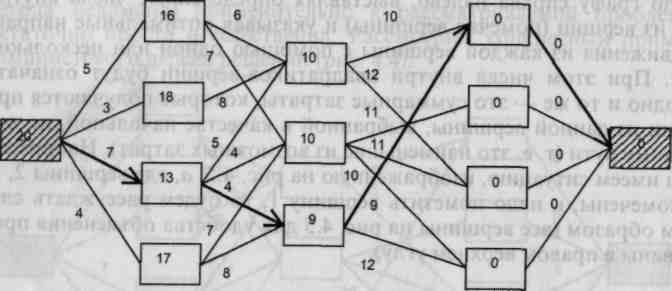
Рис. 4.6. Размеченный граф

Для восстановления искомого оптимального пути достаточно пройти теперь уже слева направо в направлении стрелок, начиная из уже поме­ченной начальной вершины (оптимальный путь на рис. 4.6 выделен). Число 20 означает минимальные возможные затраты и само оно получа­ется уже на первом этапе разметки графа. Оптимальный путь, очевидно, может быть и не единственным.

Согласно методу Беллмана одновременно находятся все возможные оп­тимальные пути. Проведенная процедура позволяет находить абсо­лютный глобальный минимум. Предыдущие рассуждения легко преобра­зуются к строгому доказательству данного утверждения. В то же время важно понимать, что глобально оптимальная стратегия не есть суперпо­зиция локально оптимальных стратегий. Скажем, при попытке построе­ния оптимального пути на графе рис. 4.6 при движении слева направо и выборе каждый раз стрелок с наименьшим весом мы, конечно, терпим неудачу и получаем результат:

3 + 8+ 10 = 21, что больше 20.