Вычислительная геометрия

1. Реализовать алгоритмы нахождения точек пересечения двух прямых, прямой и

отрезка, двух отрезков, прямой и окружности, отрезка и окружности,

двух окружностей.

2. Реализовать алгоритм определения принадлежности точки плоскому многоугольнику.

3. Реализовать алгоритм вычисления площади плоского многоугольника.

4. Реализовать алгоритм определения выпуклости плоского многоугольника.

5. Реализовать алгоритм нахождения выпуклой оболочки методом "заворачивания".

6. Реализовать алгоритм нахождения выпуклой оболочки методом Грэхема.

7[*].Записать алгоритм построения касательных, проведенных к заданной

окружности из заданной точки.

8[*].Записать алгоритм построения касательных, общих для заданной пары

окружностей.

Прямая по 2 точкам:

(x-x1)/(x2-x1)=(y-y1)/(y2-y1)

(x-x1)*(y2-y1)=(y-y1)*(x2-x1)

(y2-y1)*x+(x1-x2)*y-x1*(y2-y1)+y1*(x2-x1)=0

A=y2-y1

B=x1-x2

Ax+By+C=0

C=-A*x1-B*y1

Пересечение прямой и окружности:

Вместо формального решения системы двух уравнений подойдём к задаче с геометрической стороны (причём, за счёт этого мы получим более точное решение с точки зрения численной устойчивости). Предположим, не теряя общности, что центр окружности находится в начале координат (если это не так, то перенесём его туда, исправив соответствующе константу C в уравнении прямой). Т.е. имеем окружность с центром в (0,0) радиуса r и прямую с уравнением Ax + By + C = 0. Сначала найдём ближайшую к центру точку прямой - точку с некоторыми координатами (x0,y0). Во-первых, эта точка должна находиться на таком расстоянии от начала координат:

|C|

----------

sqrt(A2+B2)

Во-вторых, поскольку вектор (A,B) перпендикулярен прямой, то координаты этой точки должны быть пропорциональны координатам этого вектора. Учитывая, что расстояние от начала координат до искомой точки нам известно, нам нужно просто нормировать вектор (A,B) к этой длине, и мы получаем:

A C

x0 = - -----

A2+B2

B C

y0 = - -----

A2+B2

(здесь неочевидны только знаки 'минус', но эти формулы легко проверить подстановкой в уравнение прямой - должен получиться ноль) Зная ближайшую к центру окружности точку, мы уже можем определить, сколько точек будет содержать ответ, и даже дать ответ, если этих точек 0 или 1. Действительно, если расстояние от (x0, y0) до начала координат (а его мы уже выразили формулой - см. выше) больше радиуса, то ответ - ноль точек. Если это расстояние равно радиусу, то ответом будет одна точка - (x0,y0). А вот в оставшемся случае точек будет две, и их координаты нам предстоит найти. Итак, мы знаем, что точка (x0, y0) лежит внутри круга. Искомые точки (ax,ay) и (bx,by), помимо того что должны принадлежать прямой, должны лежать на одном и том же расстоянии d от точки (x0, y0), причём это расстояние легко найти:

C2

d = sqrt ( r2 - ----- )

A2+B2

Заметим, что вектор (-B,A) коллинеарен прямой, а потому искомые точки (ax,ay) и (bx,by) можно получить, прибавив к точке (x0,y0) вектор (-B,A), нормированный к длине d (мы получим одну искомую точку), и вычтя этот же вектор (получим вторую искомую точку).

Окончательное решение такое:

d2

mult = sqrt ( ----- )

A2+B2

ax = x0 + B mult

ay = y0 - A mult

bx = x0 - B mult

by = y0 + A mult

Если бы мы решали эту задачу чисто алгебраически, то скорее всего получили бы решение в другом виде, которое даёт бОльшую погрешность. Поэтому "геометрический" метод, описанный здесь, помимо наглядности, ещё и более точен.

Реализация:

double r, a, b, c; // входные данные

double x0 = -a*c/(a*a+b*b), y0 = -b*c/(a*a+b*b);

if (c*c > r*r*(a*a+b*b)+EPS)

puts ("no points");

else if (abs (c*c - r*r*(a*a+b*b)) < EPS) {

puts ("1 point");

cout << x0 << ' ' << y0 << '\n';

}

else {

double d = r*r - c*c/(a*a+b*b);

double mult = sqrt (d / (a*a+b*b));

double ax,ay,bx,by;

ax = x0 + b * mult;

bx = x0 - b * mult;

ay = y0 - a * mult;

by = y0 + a * mult;

puts ("2 points");

cout << ax << ' ' << ay << '\n' << bx << ' ' << by << '\n';

}

Пересечение 2 окружностей:

Сведём нашу задачу к задаче о пересечении окружности и прямой. Предположим, не теряя общности, что центр первой окружности - в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений:

x² + y² = r₁²

(x - x₂)² + (y - y₂)² = r₂²

Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных:

x² + y² = r₁²

x (-2x₂) + y (-2y₂) + (x₂² + y₂² + r₁² - r₂²) = 0

Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой:

Ax + By + C = 0,

A = -2x₂,

B = -2y₂,

C = x₂² + y₂² + r₁² - r₂².

Единственный вырожденный случай, который надо рассмотреть отдельно - когда центры окружностей совпадают.

Пересечение 2 отрезков:

read(x1, y1, x2, y2, x3, y3, x4, y4);

a1 := y2 - y1;

b1 := x1 - x2;

c1 := -a1 * x1 - b1 * y1;

a2 := y4 - y3;

b2 := x3 - x4;

c2 := -a2 * x3 - b2 * y3;

d := a1 * b2 - a2 * b1;

if abs(d) >= eps then

begin

dx := -c1 * b2 + c2 * b1;

dy := -a1 * c2 + a2 * c1;

x := dx / d;

y := dy / d;

if (min(x1, x2) - eps < x) and (x < max(x1, x2) + eps) and

(min(y1, y2) - eps < y) and (y < max(y1, y2) + eps) and

(min(x3, x4) - eps < x) and (x < max(x3, x4) + eps) and

(min(y3, y4) - eps < y) and (y < max(y3, y4) + eps) then

begin

writeln(1);

write(x:0:3, ' ', y:0:3);

end else write(0);

end else

begin

if abs(c1 * b2 - c2 * b1) < eps then

begin

if (abs(x1 - x3) < eps) or (abs(x1 - x4) < eps) then

begin

writeln(1);

write(x1:0:3, ' ', y1:0:3);

end else

if (abs(x2 - x3) < eps) or (abs(x2 - x4) < eps) then

begin

writeln(1);

write(x2:0:3, ' ', y2:0:3);

end else write(0);

end else write(0);

end;

Расчет площади многоугольника через сумму площадей трапеций:

for (i = 0; i < n; i++) {

if (i == 0) {

s = x[i]*(y[n-1] - y[i+1]); //если i == 0, то y[i-1] заменяем на y[n-1]

res += s;

}

else

if (i == n-1) {

s = x[i]*(y[i-1] - y[0]); // если i == n-1, то y[i+1] заменяем на y[0]

res += s;

}

else {

s = x[i]*(y[i-1] - y[i+1]);

res += s;

}

}

Выпуклый многоугольник или нет:

Для выпуклого многоугольника все векторные произведения смежных сторон будут одинакового знака, а если это не так, то будет присутствовать и произведение противоположного знака.

int Convex(XY *p,int n)

{

int i,j,k;

int flag = 0;

double z;

if (n < 3)

return(0);

for (i=0;i<n;i++) {

j = (i + 1) % n;

k = (i + 2) % n;

z = (p[j].x - p[i].x) * (p[k].y - p[j].y);

z -= (p[j].y - p[i].y) * (p[k].x - p[j].x);

if (z < 0)

flag |= 1;

else if (z > 0)

flag |= 2;

if (flag == 3)

return(CONCAVE);

}

if (flag != 0)

return(CONVEX);

else

return(0);

}

Точка в полигоне:

function otr_otr(x1, y1, x2, y2, x3, y3, x4, y4 : longint) : boolean;

var px, py, qx, qy, rx, ry : extended;

begin

if (min(x1, x2) > max(x3, x4)) or (max(x1, x2) < min(x3, x4)) or

(min(y1, y2) > max(y3, y4)) or (max(y1, y2) < min(y3, y4)) then

begin

otr_otr := false;

exit;

end;

px := x2 - x1;

py := y2 - y1;

qx := x3 - x1;

qy := y3 - y1;

rx := x4 - x1;

ry := y4 - y1;

if (px * qy - qx * py) * (px * ry - rx * py) > 0 then

begin

otr_otr := false;

exit;

end;

px := x4 - x3;

py := y4 - y3;

qx := x1 - x3;

qy := y1 - y3;

rx := x2 - x3;

ry := y2 - y3;

if (px * qy - qx * py) * (px * ry - rx * py) > 0 then

begin

otr_otr := false;

exit;

end;

otr_otr := true;

end;

function point_in_poly : longint;

var i, k : longint;

begin

if x1 <= xmin then

begin

point_in_poly := 0;

exit;

end;

for i := 1 to n do

if ((x1 - x[i - 1]) * (y[i] - y[i - 1]) = (y1 - y[i - 1]) * (x[i] - x[i - 1])) and

(min(x[i - 1], x[i]) <= x1) and (x1 <= max(x[i - 1], x[i])) and

(min(y[i - 1], y[i]) <= y1) and (y1 <= max(y[i - 1], y[i])) then

begin

point_in_poly := 2;

exit;

end;

k := 0;

for i := 1 to n do

if otr_otr(x1, y1, xmin, y1 - 1, x[i - 1], y[i - 1], x[i], y[i]) then

begin

k := k xor 1;

end;

point_in_poly := k;

end;

var i, k : longint;

begin

assign(input, 'input.txt');

assign(output, 'output.txt');

reset(input);

rewrite(output);

read(n);

xmin := 0;

for i := 1 to n do

begin

read(x[i], y[i]);

if x[i] < xmin then xmin := x[i];

end;

x[0] := x[n];

y[0] := y[n];

xmin := -abs(xmin) - 1;

read(k);

for i := 1 to k do

begin

read(x1, y1);

write(point_in_poly, ' ');

end;

end.

Выпуклые оболочки

Задача вычисления (построения) выпуклой оболочки не только является центральной в целом ряде приложений, но и позволяет разрешить ряд вопросов вычислительной геометрии, на первый взгляд не связанных с ней. Построение выпуклой оболочки конечного множества точек, и особенно в случае точек на плоскости, уже довольно широко и глубоко исследовано и имеет приложения, например, в распознавании образов [Akl, Toussaint (1978); Duda, Hart (1973)], обработке изображений [Rosenfeld (1969)], а также в задаче раскроя и компоновки материала [Freeman (1974); Sklansky (1972); Freeman-Shapira (1975)].

1. Основные понятия и идеи

Понятие выпуклой оболочки множества точек S является естественным и простым. В соответствии с определением — это наименьшее выпуклое множество, содержащее S. Чтобы наглядно представить это понятие в случае, когда S — конечное множество точек на плоскости, предположим, что это множество охвачено большой растянутой резиновой лентой. Когда лента освобождается, то она принимает форму выпуклой оболочки.

Предметом этой лекции является построение выпуклой оболочки на плоскости. Эта задача, как правило, ставится следующим образом. Задано множество S, содержащее N точек, требуется построить их выпуклую оболочку. Вашему вниманию будут представлены некоторые методы, позволяющие решить эту задачу.

Ещё одним понятием, которое нам понадобится, является понятие крайней точки. Точка выпуклого множества S называется крайней, если не существует пары точек a, b Î S таких, что p лежит на открытом отрезке ab. Множество E крайних точек S в точности совпадает с множеством вершин выпуклой оболочки S. Используя это свойство, мы приходим к основной идее алгоритма поиска:

1. Определить крайние точки.

2. Упорядочить эти точки так, чтобы они образовывали выпуклый многоугольник.

Необходима теорема, которая позволит нам проверять, является ли некоторая точка крайней.

Теорема 1. Точка р не является крайней плоского выпуклого множества S только тогда, когда она лежит в некотором треугольнике, вершинами которого являются точки из S, но сама она не является вершиной этого треугольника (рис. 12).

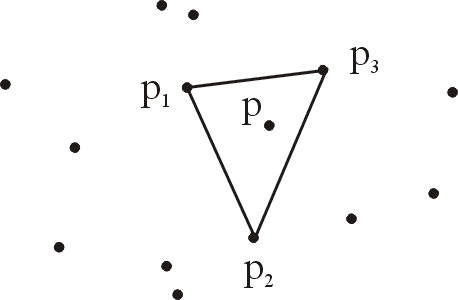
Рис. 1 Точка р не является крайней, так как она находится внутри треугольника (p₁p₂p₃).

Эта теорема дает идею для алгоритма удаления точек, не являющихся крайними. Имеется О(N³) треугольников, определяемых N точками множества S. Проверка принадлежности точки заданному треугольнику может быть выполнена за некоторое постоянное число операций, так что за время О (N³) можно определить, является ли конкретная точка крайней. Повторение этой процедуры для всех N точек множества S потребует времени O(N⁴). Хотя наш алгоритм является чрезвычайно неэффективным, он очень прост в идейном плане и показывает, что крайние точки могут быть определены за конечное число шагов.

Мы затратили время О(N⁴) только на определение крайних точек, которые должны быть как-то упорядочены, чтобы образовать выпуклую оболочку. Смысл этого порядка раскрывается следующими теоремами.

Теорема 3.5. Луч, выходящий из внутренней точки ограниченной выпуклой фигуры F, пересекает границу F в точности в одной точке.

Теорема 3.6. Последовательные вершины выпуклого многоугольника располагаются в порядке, соответствующем изменению угла относительно любой внутренней точки.

Если даны крайние точки некоторого множества, то его выпуклую оболочку можно найти, выбрав точку q, про которую известно, что она является внутренней точкой оболочки, и упорядочив затем крайние точки в соответствии с полярным углом относительно q. Сортировку можно провести за O(N log N) шагов. Таким образом мы показали, что задача поиска выпуклой оболочки может быть решена за время O(N⁴).