4.4.Численное дифференцирование и интегрирование
К численному
дифференцированию приходиться прибегать
в том случае, когда функция f(x),
для которой нужно найти производную,
задана таблично или же функциональная
зависимость f(x)
имеет сложное аналитическое выражение.
В этих случаях функция разбивается
одномсерной сеткой
и используются приближенные формулы.
Формула первой производной для двух
узлов:
(4.4.1),
, h-шаг
изменения аргумента.
Формула первой производной по трем узлам для второй точки:
(4.4.2)
, где
Формула второй производной для трех узлов:
(4.4.3)
Численное
интегрирование применяют в случаях
когда нельзя найти формулу первообразной
в элементарных функциях. Общий метод
численного интегрирования сводится к
замене интегрируемой площади
подынтегральной функции на элементарные
площади, получаемые разбиением с заданным
шагом
, где
–
квадратурная сумма,
-коэффициенты,
-узлы
квадратурной функции.
Формула прямоугольников.
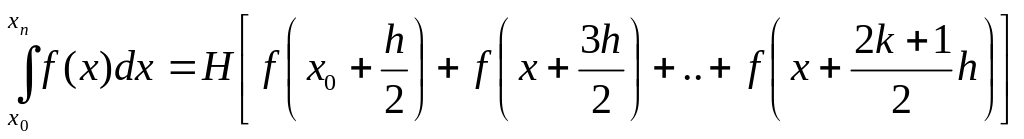(4.4.4),
где
(k-
число разбиений).
Иллюстрация метода прямоугольников.
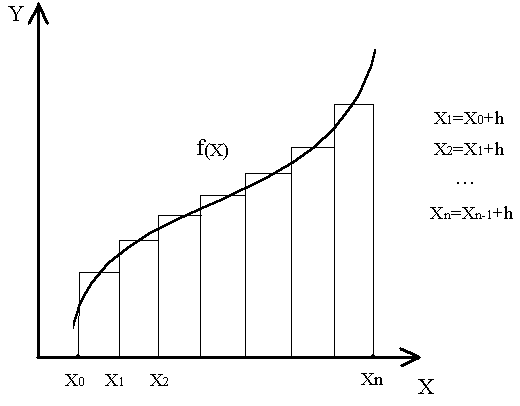
Формула трапеций.
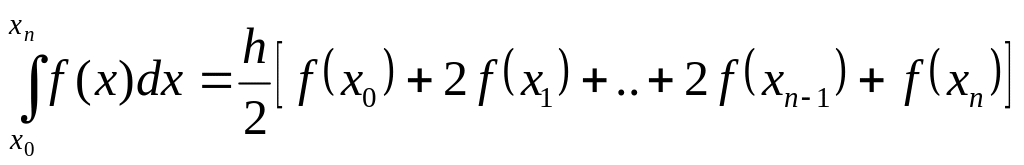(4.4.5)
где h-шаг разбиения
Ошибка вычисления интеграла определяется как
,
где
Иллюстрация метода трапеций.
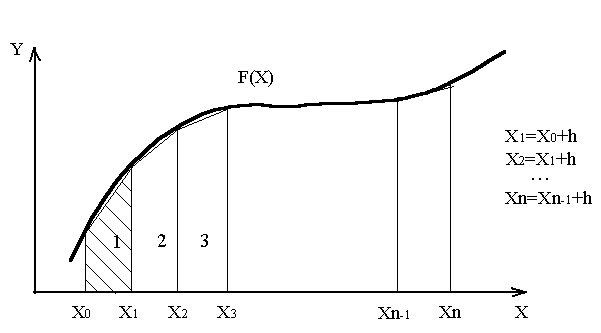
Формула Симпсона.
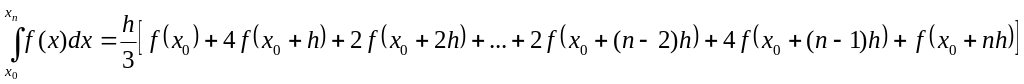(5.4.6
), где
(n-число
разбиений)
Ошибка вычисления интеграла
где
,
четвертая
производная.
Рассмотрим
численный метод вычисления интеграла
с шагом 0.01 по формуле Симпсона.
Интеграл
будет иметь вид :
=
Пример.
Написать алгоритм и программу вычисления
интеграла
на основе метода прямоугольников и
найти первую производную по двум узлам
и вторую производную выражения
по двум узлам 2 и 4.
Обозначим в схеме выражения (4.4.2), (4.4.3), (4.4.4) соответственно (a), (b), (c)
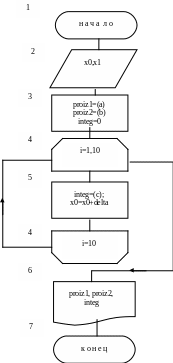
var
delta:real;
x0,x1,n,proiz1,proiz2,integ:real;
i : integer;
function fun(x:real):real;
begin
fun:=12*x*x+exp(x);
end;
Begin
write('Введите x0 и x1:');
readln(x0,x1);
n:=x0;
proiz1:=fun(x1)-fun(x0)/(2*abs(x1-x0)); {вычисление первой производной}
proiz2:=(fun(x0)-2*fun(x0+abs(x1-x0)/2)+fun(x1))/(abs(x1-x0)*abs(x1-x0));
{вычисление второй производной}
delta:=abs(x1-x0)/10;
integ:=0;
for i:=1 to 10 do begin
integ:=integ+delta*(fun(x0)+fun(x0+delta))/2; {вычисление интеграла}
x0:=x0+delta;
end;
writeln('Первая производная=',proiz1:6:2,’ в точке x=’,(x1-n)/2);
writeln('Вторая производная=',proiz2:6:2,’ в точке x=’,(x1-n)/2);
writeln('Интеграл=',integ:6:2);
readln;
End.
Результаты задачи 4 :
Введите x0 и x1 : 2 4
Первая производная=232.75 в точке x=3
Вторая производная=11.45 в точке x=3
Интеграл=271.53
4.5.Методы решения дифференциальных уравнений. Метод Рунге-Кутта
Дифференциальным уравнением 1-го порядка называется уравнение вида:
(4.5.1)
Решить дифференциальное уравнение это значит определить функцию y=F(x), которая при подстановке в уравнение (4.5.1) приводит к тождеству. Поиск решения y=F(x) при реализации аналитических методов сводится к интегрированию уравнения (4.5.1), что не всегда приводит к успеху из-за сложности вида f(x,y). Поэтому для решения задач (4.5.1) используют численные методы.
Метод Эйлера. При реализации метода Эйлера для уравнения (4.5.1) первую производную заменяют приближенным соотношением:
,
(4.5.2)
которое является первым приближением формулы Тейлора:
Таким образом, уравнение (4.5.2) преобразуется к виду:
(4.5.3)
где
.
Для
решения уравнения (4.5.1) с помощью
приближения (4.5.3) вводят начальное
условие Коши
.
Поясним
применимость формулы (4.5.3) для решения
дифференциального укравнения
на отрезке [1,3] при начальном условии
y(x=1)=2.
Выберем шаг итерации 0.5:
y(1)=2;
Отсюда
y(1)=2;
y(1.5)=2+0.5*(2*2+e)=5.39;
y(2)=5.39+0.5*(2*5.39+
)=13.1;
y(2.5)=13.1+0.5*(2*13.1+
)=43.17;
y(3)=43.17+0.5*(2*43.17+
)=92.79.
Результаты вычислений представлены в таблице
k |
|
|
|
|
0 |
1 |
2 |
- |
- |
1 |
1.5 |
5.39 |
3.39 |
2 |
2 |
2 |
13.1 |
7.71 |
5.39 |
3 |
2.5 |
43.17 |
30.07 |
13.1 |
4 |
3 |
92.79 |
49.62 |
43.17 |
Метод Рунге-Кутта четвертого порядка.
Итерационная формула в этом методе имеет вид:
(4.5.4),
где
;
;
;
.
Поясним применимость метода Рунге-Кутта четвертого порядка для решения уравнения на отрезке [1,3] с начальными условиями y(x=1)=2.
Выберем шаг 1:
;
;
;
;
;
для следующего шага:
;
;
;
;
;
Обозначим
.
Результаты вычислений представлены в
таблице:
k |
|
|
|
|
0 |
1 |
2 |
- |
- |
1 |
2 |
26.27 |
24.27 |
2 |
2 |
3 |
201.3 |
175.03 |
26.27 |
Для
решения дифференциального уравнения
более высокого порядка
используется следующий прием. Любое
уравнение n-го
порядка можно свести к системе n
уравнений первого порядка способом
замены переменных. Для этого вводят
новые переменные
,
в результате чего получают эквивалентную
систему:
Указанный метод позволяет свести решение дифференциального уравнения n-го порядка к решению системы n уравнений первого порядка. В свою очередь методы решения одного уравнения первого порядка распространяются на систему таких уравнений.
Рассмотрим
данный метод на примере дифференциального
уравнения
с начальными условиями
,
на отрезке [1,3].
Выполним
замену переменной
и приходим к системе из двух уравнений:
Таким образом любое уравнение n-порядка можно свести к системе уравнений первого порядка.
Пример. Написать алгоритм и программу решения дифференциального уравнения на отрезке [0,2] методом Рунге-Кутта четвертого порядка. Начальное условие Коши y(0)=1.
Обозначим выражение (4.5.4) в схеме алгоритма как (a).
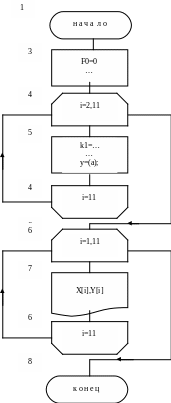
program Runge_Cutta;
uses crt;
var y,x: array [1..11] of real;
k1,k2,k3,k4,y0,h,f0,fn:real;
i:integer;
function fun(x,y:real):real;
begin
fun:=2*y+exp(x);
end;
begin {н.п.}
clrscr;
f0:=0;
fn:=2;
h:=abs(fn-f0)/10; {шаг}
y0:=1;k1:=0;k2:=0;k3:=0;k4:=0;
k1:=fun(f0,y0);
k2:=fun(f0+h/2,y0+h*k1/2);
k3:=fun(f0+h/2,y0+h*k2/2);
k4:=fun(f0+h/2,y0+h*k3/2);
y[1]:=y0+(h/6)*(k1+2*k2+2*k3+k4); {вычисление функции в первой
точке}
x[1]:=f0;
f0:=f0+h;
for i:=2 to 11 do begin
k1:=fun(f0,y[i-1]);
k2:=fun(f0+h/2,y[i-1]+h*k1/2);
k3:=fun(f0+h/2,y[i-1]+h*k2/2);
k4:=fun(f0+h/2,y[i-1]+h*k3/2);
y[i]:=y[i-1]+(h/6)*(k1+2*k2+2*k3+k4); {вычисление функции в
остальных точках}
x[i]:=f0;
f0:=f0+h;
end;
for i:=1 to 11 do
writeln('x[',i,']=',x[i]:2:1,' y[',i,']=',y[i]:5:3);
readln;
end.{к.п.}
Результаты задачи 5:
x[1]=0.0 y[1]=1.733 x[2]=0.2 y[2]=2.870
x[3]=0.4 y[3]=4.618 x[4]=0.6 y[4]=7.282
x[5]=0.8 y[5]=11.315 x[6]=1.0 y[6]=17.391
x[7]=1.2 y[7]=26.510 x[8]=1.4 y[8]=40.151
x[9]=1.6 y[9]=60.505 x[10]=1.8 y[10]=90.814
x[11]=2.0 y[11]=135.871