Глава 3. Спектральный анализ сигналов

Теорема Фурье гласит, что любой сигнал можно разложить в ряд по ортонормированному набору периодических функций (например, по синусам и косинусам) с частотами кратными частоте периодического сигнала. Таким образом, в основе спектрального анализа сигнала лежит поиск весовых коэффициентов (в общем случае комплексных), модуль которых соответствует доли мощности колебаний соответствующей гармоники, вносимой в общую суперпозицию всех гармоник.

3.1. Быстрое преобразование Фурье

Быстрое преобразование Фурье – это алгоритм вычисления, который успешно использует свойства периодичности тригонометрических функций для того, чтобы избежать ненужных вычислений в дискретном преобразовании Фурье (ДПФ), за счёт чего быстрее осуществляется поиск коэффициентов в разложении Фурье. Основное отличие от дискретного преобразования заключается лишь в методе вычисления числовых значений (алгоритме), а не в самой обработке сигнала. И в случае БПФ, и в случае ДПФ результат вычислений один и тот же [16]. Единственным требованием для алгоритма БПФ является размер выборки, кратный N = 2^L, где L – любое положительное целое число. Наиболее распространёнными алгоритмами БПФ по основанию 2 являются: с прореживанием по времени и с прореживанием по частоте.

В данной работе реализован алгоритм БПФ по основанию 2 с прореживанием по времени (алгоритм Кули – Тьюки). Его легко получить, исследуя некоторые закономерности ДПФ. Введём так называемый поворотный коэффициент:

( 1)

В этом случае в ДПФ коэффициенты Фурье для ряда значений сигнала {f₀,f₁,…,f_N-1} выражаются соотношением:

(2)

Рассмотрим ряд сигнала из 4 значений: {f₀,f₁,f₂,f₃}. Представим преобразование Фурье в матричном виде (нормировочный коэффициент 1/N внесён в вектор-столбец С_ij в правой части выражения):

(4)

Расписав поворотные коэффициенты по формуле Эйлера и определив их значения при k = 0, 1, 2,.. 9, можно построить диаграмму (Рис. 2), из которой видна закономерность повторяющихся коэффициентов.

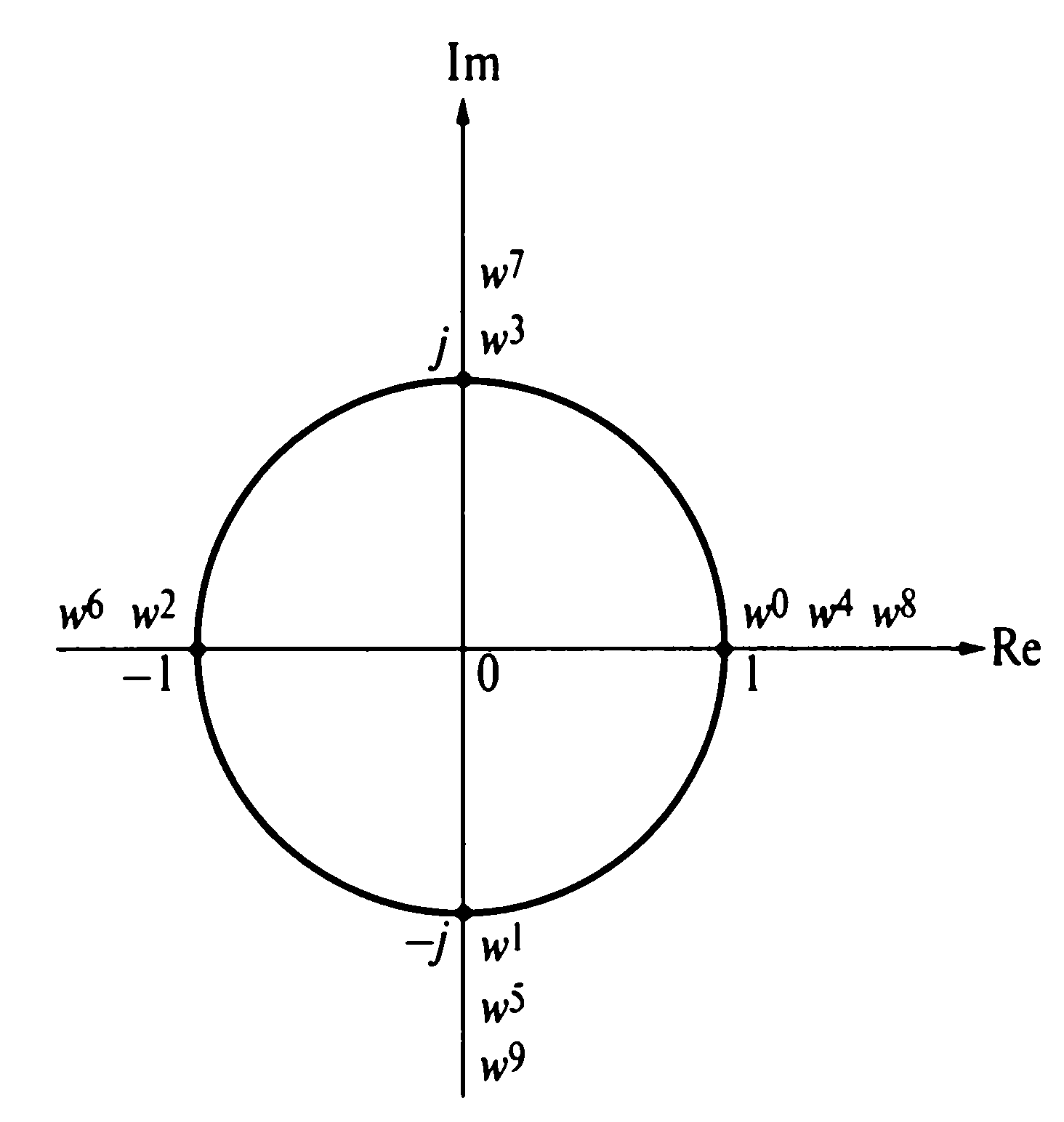
Рисунок 2. Степенной ряд w для N=4

Подставляя численные значения в (4) получим:

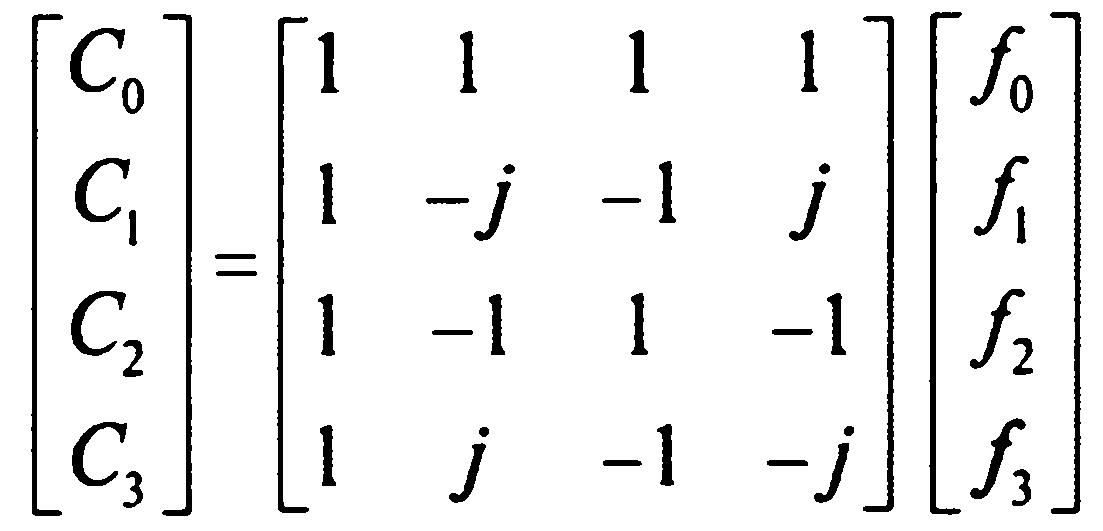
(4*)

То есть значения w, начиная с w⁴, равны соотвествующему значению от w⁰ до w³. Далее перепишем матричное уравнение (4) в нестандартном виде (подобные обозначения введены для наглядности дальнейших операций):

(5)

П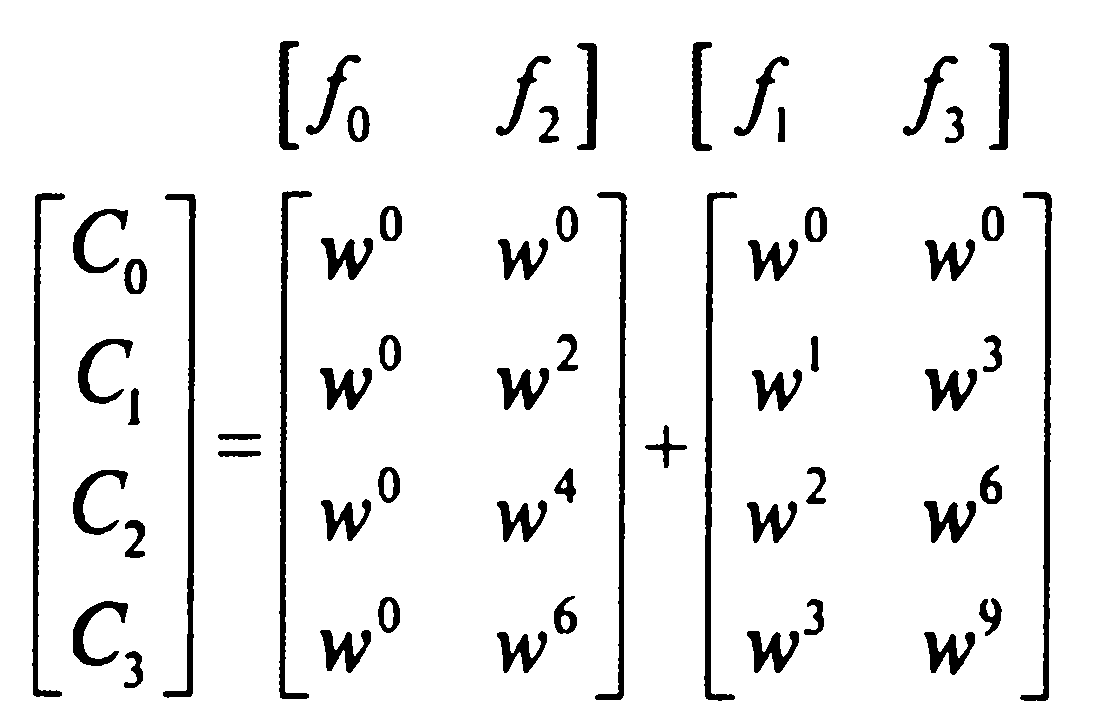 оменяем местами столбцы матрицы, разделив её на две группы: по чётным f₀, f₂ и нечётным f₁, f₃ индексам:

(6)

Учтём, что w^k+1 = w^kw¹, тогда выражение (6) перепишется в виде:

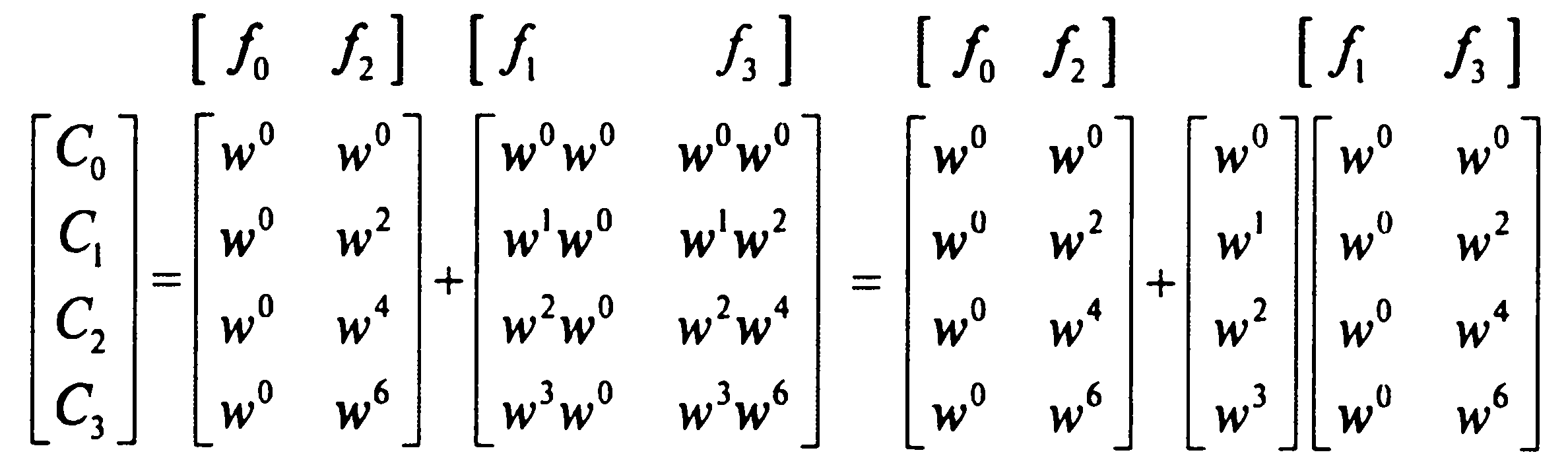
(7)

Используя соотношения:

( 8)

( 9)

Получаем искомые коэффициенты разложения в виде вектора-столбца со значениями ячеек:

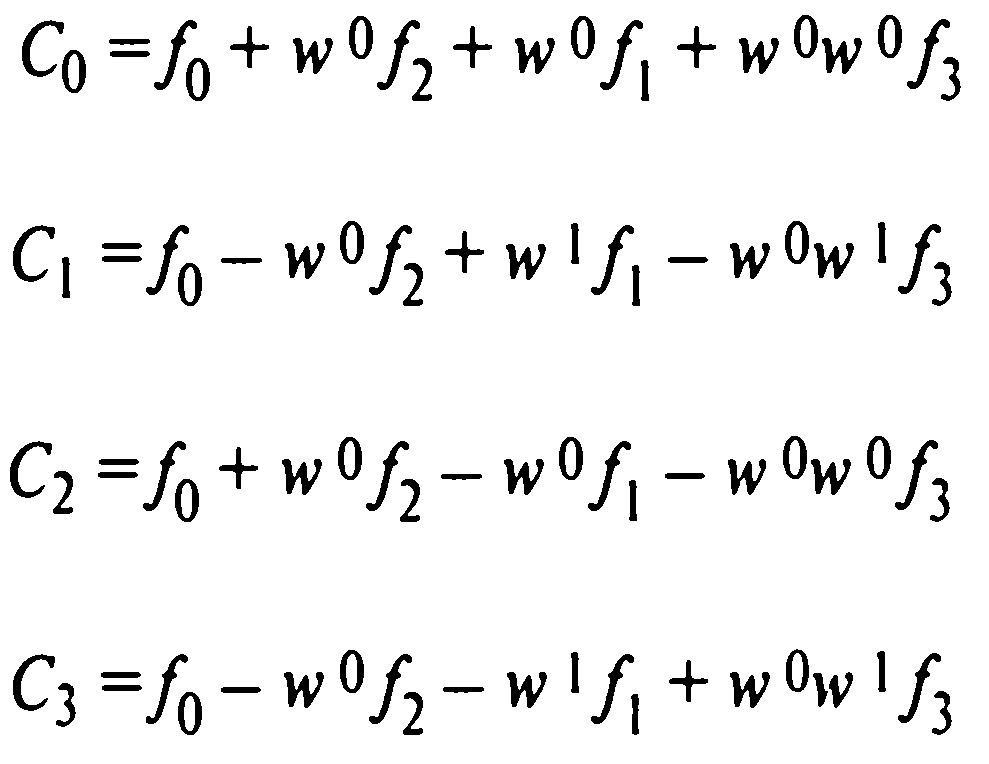
(10)

Графическое изображение алгоритма (Рис. 3) похоже на бабочку с распахнутыми крыльями, поэтому этот метод вычисления называют «бабочкой».

Рисунок 3. Граф «Бабочка» для ряда из 4 членов

Итак, на первом шаге алгоритма идёт разбиение по чётным и нечётным индексам членов ряда значений сигнала. Затем выполняется граф «бабочка», он состоит из двух ступеней, их количество равно степени двойки объёма выборки (N = 4 = 2²). На каждом ступени выполняется по две «бабочки» и их общее количество неизменно. Каждой операции «бабочка» соотвествует одна операция умножения. Для сравнения: в ДПФ с выборкой {f₀,f₁,f₂,f₃} операцию умножения необходимо было бы выполнить 4×4 = 16 раз, а в случае БПФ всего лишь 4 раза [16].