1). Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
Функция
F(x)
наз. первообразной
для функции f(x)
на интервале (a,b),
если F(x)
дифференцируема на [a,b]
и
.
Множество
всех первообразных для данной ф-ции
наз. неопределенным
интегралом (НИ):
.
Свойства
НИ:
,
,
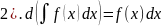Таблица
интегралов:
,
,
,
,
,
,
,
,
.
Доп.
св-ва НИ:
,
.
,
,
.
2).Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
,
,
t
– новый аргумент; имеет обратную:
t=ψ(x),
.
,
f(x)-
произвольная ф-ция
.
Интегрирование
по частям:
.
Отметим, что метод применим к интегралам:
и к инт-ам, содержащим обратные триг.
ф-ции. Если подинт. выражение содержит
многочлен, то этот многочлен берется
за u,
все ост. – dv.
Если подинт. выражние содержит arcsin,
arccos,
т.е. трансценд. ф-ции, то эта ф-ция
выбирается в кач. u,
то же самое относится и к степеням
трансц. ф-ции. Если встречается многочлен
и тр. ф-ция, то u=многочлен.
3).
Интегрирование дробей вида:
;
;
;
,
где
.
1).
,
2).
,
3).
.
4).
,
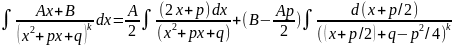последний инт-л по рекуррентной ф-ле
приведется к интегралу
:
.
4).
Интегралы вида:
и
.
этот
инт-л можно привести к инт-лу от
рациональной ф-ции, введя замену:
,
q
– наименьший общий знаменатель дробей:
.
инт-л
приводится к инт-лу от рац. ф-ции
подстановкой:
,
s-наименьший
общий знаменатель дробей:
.
5).
Интегралы вида:
,
.
.
.
Последний инт-л был уже рассмотрен.
6). Интегралы вида: , .
Выделяем
полный квадрат в подкоренном выражении,
чтобы привести инт-л к табличному: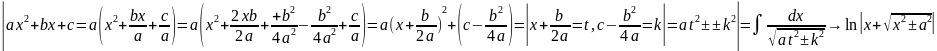
.
Пример:
.
7). Интегралы вида: .
9). Тригонометрические подстановки при нахождении неопределённых интегралов.
I).
II).
III).
,
т.о. придем к инт-лу рац. ф-ции.
IV). Если подинт. ф-ция зависит только от tgx (или ее можно привести к такому виду), то: tgx=t.
V).
Если sin
и cos
в четных степенях, то tgx=t,
,
.
VI).
.
.
.
Для
нахождения каждого из интегралов с
такими ф-лами используются эти
преобразованиями.
VII).
.
VIII).
IX).
.
8). Интегрирование дифференциальных биномов.
рац.
числа. П.А. Чебышев показал, что этот
инт-л может быть выражен в простых
ф-циях в 3-х случаях:
1.p-целое
число -> x=
,
s-общий
знам. m
и n.
2.
– целое число:
,
q
– знаменатель др. p.
3.
– целое число:
,
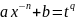q
– знаменатель др. p.
10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
Криволинейная
трапеция – фигура,
ограниченная линиями. y=f(x),
x=0,
x=a,
x=b.
Подсчитаем S
криволин. трап. хотя бы прближенно: 1).
отрезок [a,b]
разобьем точками деления
=b.
.
2). внутри кажд. отрезка
произвольным
образом
выберем т-ку
и проведем к ней ┴ до пересечения с
дугой AB.
- интегральная сумма. Тогда площ. всей
криволинейной трапеции:
,
если этот предел сущ-т и не зависит от
способа разбиения отрезка [a,b]
на части, ни от выбора точек
в кажд. части, то он наз-ся определенным
интегралом от ф-ции f(x)dx
на отрезке [a,b].
Т.о. с геометрич. точки зрения введенный
интеграл, представляет собой S
криволин. трапеции:
.
Теорема
1.
Если ф-ция f(x)
непрерывна на [a,b],
то она интегрируема на нем. По определению:
.
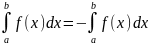Основные св-ва ОИ (опред. инт-л): 1.
,
2.
,
3. если на [a,b]
2 непрерывных ф-ции f(x)
и
удовлетворяют
,
то
,
4. если m
и M
есть соответственно наименьшее и
наибольшее значения ф-ции f(x)
на [a,b],
M(b-a)
,
5. ТЕОРЕМА
О СРЕДНЕМ: если
f(x)
интегрируема на [a,b],
то внутри этого отрезка, то внутри [a,b]
есть точка
:
,
– среднее значение ф-ции f(x)
на [a,b].
– S
прямоуг. тр., основание кот. явл-ся ab,
а высотой
.
6.
для любых точек a,b,c
имеет место быть равенство:
.рис->
7.если
f(x)
–четная ф-ция, то
.
8.если
f(x)
– нечетная ф-ция, то
.
Вычисление
ОИ. Ф-ла Ньютога-Лейбница. Интеграл
с переменным верхним пределом:
.
Теорема: производная от инт-ла с
переменным верхним пределом = подинт.
ф-ции, в кот. вместо переменной
интегрирования подставлено значения
верхнего предела. На основании этой
теоремы получили ф-лу, дающую возможность
вычислить ОИ (эта ф-ла устанавливает
связь между НИ и ОИ). Пусть есть
– ф-ла
Ньютона-Лейбница.
,
.