САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физический факультет

Кафедра электроники твердого тела

Г.Г.Владимиров

ФИЗИЧЕСКАЯ ЭЛЕКТРОНИКА

Часть II. Эмиссия в сильных электрических полях

Учебно-методическое пособие

Санкт Петербург

2012 г.

ОГЛАВЛЕНИЕ

3.1.		Уравнение Фаулера-Нордгейма для автоэмиссионного тока с металлов	3.3
3.2.		Эффект Ноттингама	3.13
3.3		Экспериментальные исследования АЭЭ	3.16
3.4.		Особенности автоэлектронной эмиссии с полупроводников	3.25
3.5.		Эмиссия электронов из системы МДМ. Эффект Малтера		3.34
3.6.		Взрывная эмиссия	3.45
3.7.		Практическое использование автоэлектронной эмиссии	3.50
	3.7.1.	Изучение поверхностных явлений при помощи автоэлектронного микроскопа (АЭМ)	3.50
	3.7.2.	Применение автокатодов в технике	3.54
3.8.		Сканирующая туннельная микроскопия	3.62
3.9.		Микроскоп атомных сил (МАС)	3.72
		Рекомендуемая литература	3.80
		Цитированная литература	3.80

При наличии в системе сильного электрического поля становится возможной эмиссия электронов. Первое упоминание о таком явлении относится к 1897 г. Было обнаружено появление тока при поле, тянущем отрицательные заряды от поверхности. Дальнейшие исследования показали, что имеет место эмиссия электронов. Это явление впоследствии получило название автоэлектронная эмиссия (field emission). Обычно для получения измеримых токов необходимы поля F = 10⁶ -10⁷ В/см. Важной особенностью этого вида эмиссии является то, что эмиссионный ток может быть получен при любых, сколь угодно низких температурах. Физический механизм эмиссии электронов удалось понять после разработки квантово механической теории, на базе которой Фаулером и Нордгеймом в 1928 г. было создано математическое описание процесса эмиссии электронов из металлов [1]. В дальнейшем было показано, что выход электронов в вакуум возможен и в тех случаях, когда удается создать сильные электрические поля внутри твердого тела. Начнем с наиболее простого случая – автоэмиссии электронов с металлов.

3.1. Уравнение Фаулера-Нордгейма для автоэмиссионного тока с металлов

Р

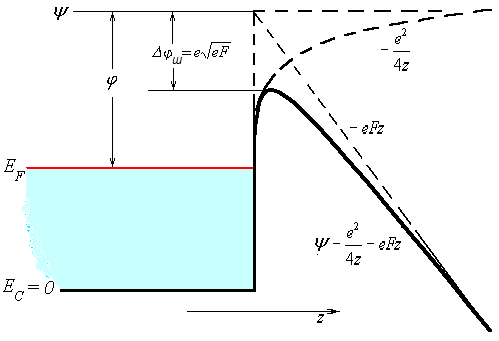
Рис.3.1.1.При наличии у поверхности металла однородного электрического поля потенциальный барьер имеет форму, близкую к треугольной. Имеется возможность туннелирования электронов в вакуум при высоких полях.

ассмотрим энергетическую схему металла, для описания которого, как и прежде, используем модель Зоммерфельда (рис.3.1.1). Будем считать, что наш металл находится при Т=0 К. Электроны заполняют все состояния, находящиеся между дном зоны проводимости E_C и уровнем Ферми E_F. В данном случае удобно принять за ноль энергию, соответствующую дну зоны проводимости. Энергию уровня вакуума обозначим величиной , т.е. работа выхода  =  - E_F. Пусть у поверхности имеется однородное электрическое поле напряженностью F. Тогда потенциальная энергия электрона в вакууме равна следующей величине:

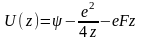(3.1.1)

В

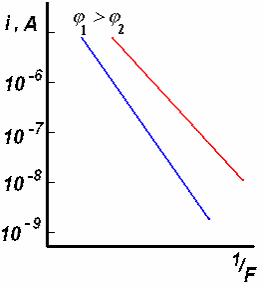
Рис.3.1.2.Схематическое представление зависимости автоэмиссионного тока от напряженности электрического поля. Прямые тем круче, чем больше работа выхода эмиттера.

следствие наличия сил зеркального изображения высота барьера, препятствующего выходу электронов из твердого тела понижается на величину _ш =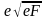 (раздел 1.3.4). Можно было думать, что автоэмиссия как раз и связана с этим понижением. Однако, для этого необходимо выполнение условия _ш > , что требует чрезвычайно большой напряженности электрического поля. Действительно, если подставить константы в выражение для шоттковского понижения  (1.3.17), то получим _ш(эВ) = 3.8*10^-4 F(В/см). Таким образом, для выполнения указанного условия необходимы поля, превышающие 10⁸ В/см. Между тем эмиссия электронов значительной величины наблюдается при существенно более низких F (10⁶-10⁷ B/см). Кроме того, наблюдается очень сильная зависимость от напряженности электрического поля. Если представить экспериментальные данные в виде зависимости ln i = f (1/F), то получается прямая линия, причем при изменении тока на несколько порядков (рис.3.1.2). Наклон прямых зависит от работы выхода эмиттера и тем круче, чем она выше. Такое поведение существенно отличается от наблюдаемого в случае термоэлектронной эмиссии. Объяснить эмиссию электронов в данном случае можно только квантово-механическим эффектом туннелирования.

Рассмотрим эмиссию из металла, для которого будем считать справедливой модель свободных электронов. Выражение для потока электронов, падающих на поверхность рассматривалось ранее (раздел 1.2). Величина эмиссионного тока может быть вычислена, если известна зависимость прозрачности барьера D от энергии электронов. Величина D зависит от компоненты энергии, соответствующей движению электрона по нормали к поверхности E_{z ,} и может быть выражена, как показано в квантовой механике, следующим образом:

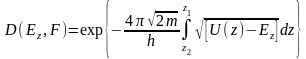(3.1.2)

где h – постоянная Планка, m – масса электрона. z₁ и z₂ - точки поворота движения электрона, определяемые из соотношения U( z_i ) - E_z= 0. Это выражение справедливо для D(E_z,F)<1/e, т.е. может быть использовано в случае не чрезмерно высоких полей. Интеграл в показателе экспоненты, если подставить (3.1.1), аналитически не вычисляется. Этому препятствует член, связанный с силами зеркального изображения. Интеграл вычисляется, если пренебречь его наличием, т.е. считать потенциальный барьер треугольным. Определяя z₂ из (3.1.1) без учета второго слагаемого и считая z₁=0, получим:

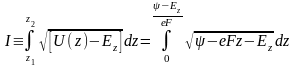(3.1.3)

Интегрирование элементарно, что становится очевидным, если воспользоваться новой переменной t =  - eFz - E_z:

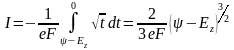(3.1.4)

Таким образом, прозрачность треугольного барьера:

(3.1.5)

В действительности необходимо учитывать наличие сил зеркального изображения – они оказывают значительное влияние на форму барьера. Нордгейм предложил и в этом случае записывать прозрачность барьера похожим образом, но ввести в показатель экспоненты так называемую функцию Нордгейма (у):

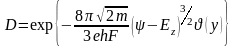(3.1.6)

Аргументом функции Нордгейма является отношение шоттковского понижения в поле _ш к энергии относительно уровня вакуума, т.е.

(3.1.7)

Ф

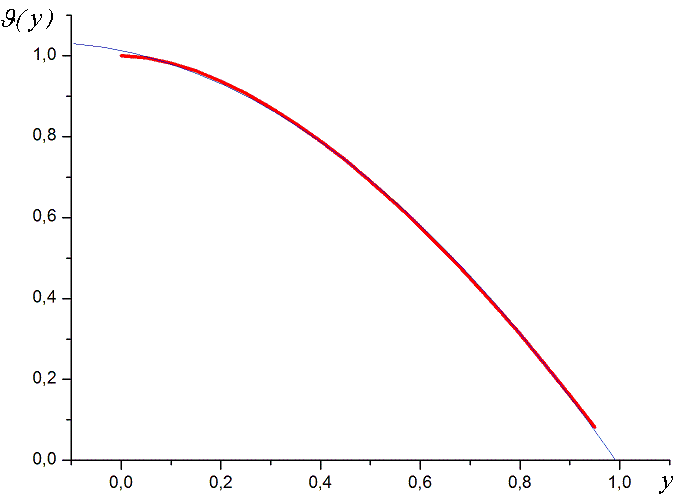
Рис.3.1.3.Зависимость функции Нордгейма от аргумента [2].

ункция была вычислена численно [2], ее зависимость от аргумента приведена на рис.3.1.3. Приближенно она может быть описана полиномом:

(y) = 1,01231 - 0.255 y - 0,772 y² (3.1.8)

Знание прозрачности барьера позволяет рассчитать эмиссионный ток. Используем, как и ранее, распределение электронов по импульсам (1.3.3) и напишем выражение для потока эмитированных электронов с заданным значением компонентов импульса в следующем виде:

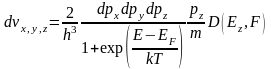(3.1.9)

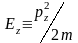
к

(3.1.10)

оторое перепишем, учтя тождество :

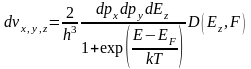
Наибольший интерес представляет распределение электронов по полной энергии N(Е). Перейдем к новым переменным E, p_||, , которые введем следующим образом:

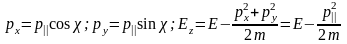
(3.1.11)

Как известно, при замене переменных элементарный объем можно рассчитать используя якобиан:

(3.1.12)

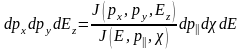
В свою очередь:

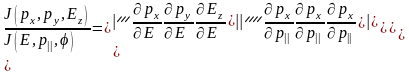
(3.1.13)

Итак:

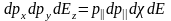(3.1.14)

Количество электронов, обладающих энергией в интервале (E, E+dE), получим, если проинтегрируем по всем возможным  и р_||. Пределы интегрирования очевидны: по  от 0 до 2, по p_|| от 0 до 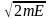. В результате получаем для распределения электронов по полным энергиям:

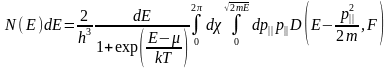(3.1.15)

Интегрирование по углу  тривиально. Сложнее выполнить интегрирование по р_||, поскольку интеграл не берется в простых квадратурах. Его можно рассчитать приближенно, используя разложение показателя экспоненты в ряд. Положим:

(3.1.16)

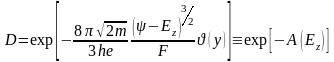Очевидно, что наибольший вклад в эмиссионный ток дают электроны, имеющие энергию, близкую к энергии уровня Ферми. Поэтому разложим функцию A(E_z) в ряд вблизи E_F:

A(E_z) = (E_F) - (E_F) (E_z-E_F)+(E_F) (E_z-E_F)² + … (3.1.17)

где

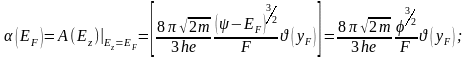(3.1.18)

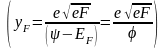(3.1.19)

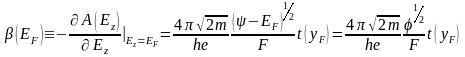(3.1.20)

(3.1.21)

(3.1.22)

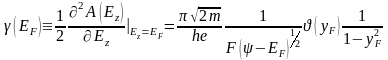
Последним слагаемым в (3.1.17) можно пренебречь ввиду его малости. Подставляя полученное выражение в (3.1.15) и вводя новую переменную 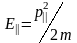получим выражение для распределения автоэлектронов по полным энергиям:

(3.1.23)

На рис.3.1.4 приведена теоретическая зависимость N(E) (пунктирная кривая). Для сравнения на нем же представлена зависимость, полученная Э.Мюллером с сотр. в первой работе, посвященной исследованию этого вопроса [3]. Учитывая неизбежное размытие экспериментальной зависимости вследствие ограниченной разрешающей способности прибора, согласие очень хорошее. Зависимость N(E) имеет максимум, положение которого может быть легко определено. Для этого достаточно продифференцировать N(E) по энергии и приравнять результат нулю:

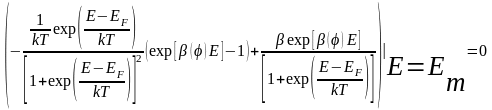
или:

(3.1.24)

Нетрудно убедиться, что  имеет большое численное значение:

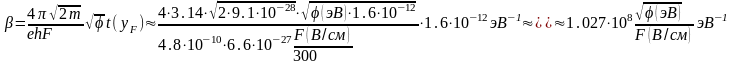
(3.1.25)

Учитывая, что при автоэлектронной эмиссии наиболее важны состояния электронов с энергиями близкими к уровню Ферми, а он располагается на несколько эВ выше дна зоны проводимости, очевидно, что:

exp(- E_т)<<1 (3.1.26)

Это позволяет пренебречь экспонентой в левой части (3.1.24). В результате получим:

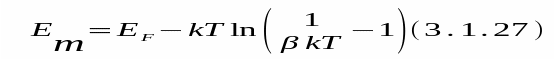
При Т=300 К и ~10 эВ^-1 имеем:

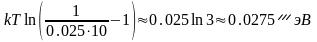
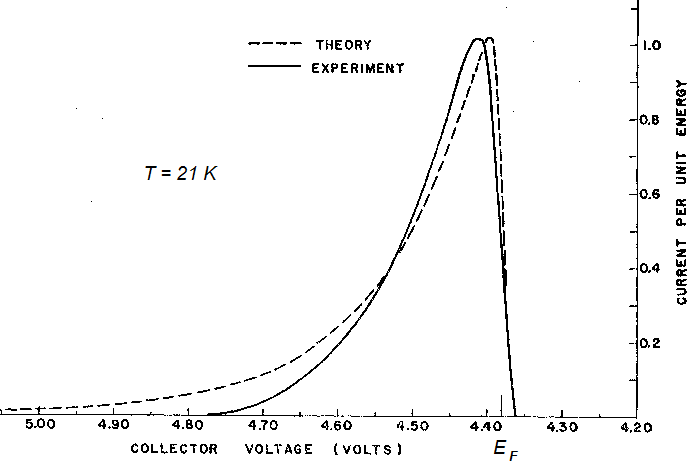Рис.3.1.4. Распределение автоэлектронов по полным энергиям: штриховая кривая – теоретическая, сплошная – экспериментальная. По шкале энергий отложено напряжение на коллекторе, уровню Ферми соответствует V=_А. Большие значения V соответствуют меньшим энергиям автоэлектронов. [3].

(3.1.28)

т.е. несколько сотых эВ. Таким образом, максимум кривой распределения электронов по энергиям практически совпадает с энергией уровня Ферми.

Часто для характеристики дисперсии какой-либо величины вводят понятие полуширины распределения, под которой понимают ширину на полувысоте максимума - . При Т=0 для этой величины получается простое выражение:

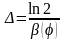(3.1.29)

Т.е. крайне малая величина. В частности, в случае вольфрама имеем: =140 мэВ,.что значительно меньше, чем в случае термоэмиссии. Это обстоятельство определяет перспективность использования автокатодов в электроннолучевых устройствах.

Если известно N(E), то можно вычислить величину тока автоэмиссии:

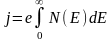(3.1.30)

Подставляя в это выражение величину N(E) из (3.1.23) и интегрируя по всем возможным энергиям, имеем:

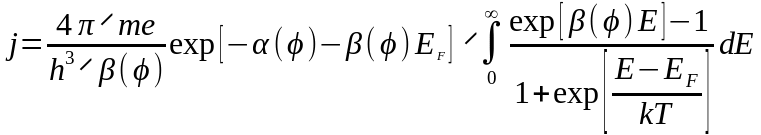(3.1.31)

Интеграл в простых квадратурах не берется, но его можно вычислить в хорошем приближении. Для этого разобьем его на два:

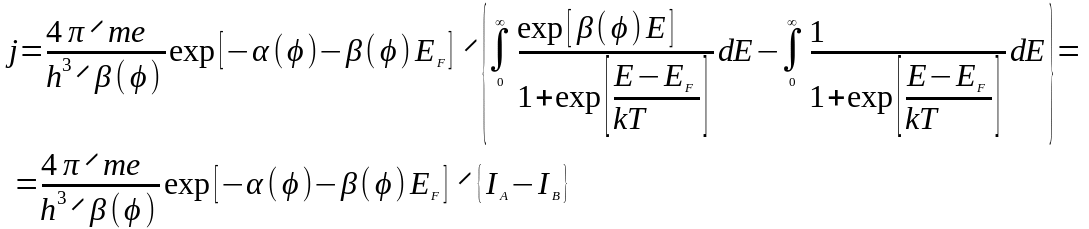(3.1.32)

и вычислим сначала первый:

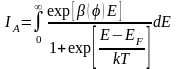(3.1.33)

Сделаем замену переменных:

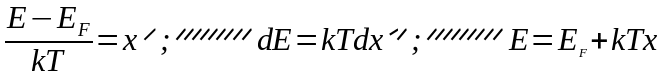(3.1.34)

тогда:

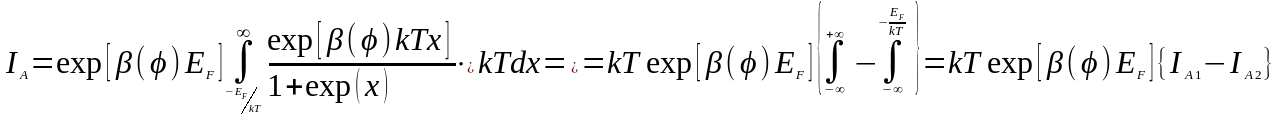
(3.1.35)

Первый из интегралов в фигурной скобке сводится к табличному, если воспользоваться подстановкой exp(x)=t [4, с.299 (3.194.4)]:

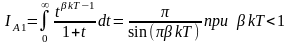(3.1.36)

Второй можно вычислить используя ту же замену переменных и воспользовавшись тем, что величина t имеет малую величину. Это позволяет разложить подынтегральное выражение в ряд:

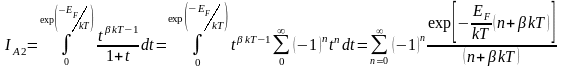(3.1.37)

Поскольку E_F >> kT, эта величина является лишь малой поправкой к величине I_A1.

Остается вычислить интеграл I_B, который может быть получен элементарным интегрированием, если воспользоваться той же заменой переменных (3.1.34):

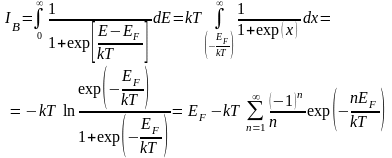
(3.1.38)

В результате, для плотности полного тока автоэмиссии имеем:

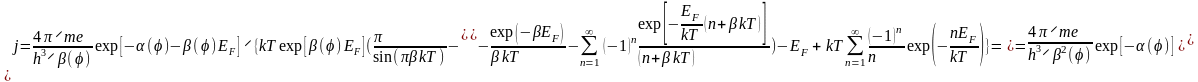
(3.1.39)

Как уже отмечалось выше,  имеет достаточно большую величину (порядка 10 эВ^-1). E_F даже в случае металлов с невысокой плотностью электронного газа равна нескольким эВ, и следовательно exp(-E_F) мала. Это позволяет упростить выражение - пренебречь вторым и третьим слагаемыми в фигурных скобках, поскольку первое слагаемое явно несколько превышает единицу. В результате, используя выражения для  и  (3.1.18 и 3.1.20), имеем:

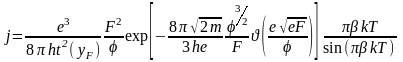
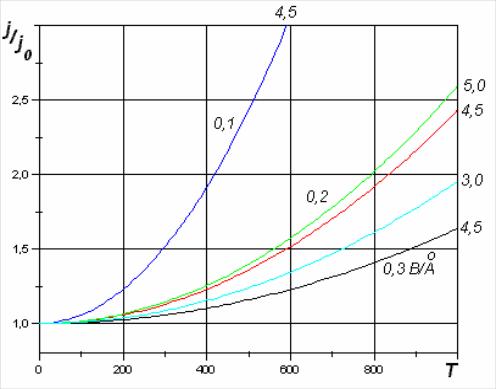
Рис.3.1.5.Зависимость автоэмиссионного тока от температуры при различных напряженностях электрического поля. Около концов кривых указана величина работы выхода автоэмиттера в эВ. j₀ – ток при Т=0 К.

(3.1.40)

Обычно его записывают в более простой форме, пользуясь тем, что величина функции t(y_F) слабо зависит от напряженности поля и практически равна единице (также как и функция Нордгейма t(y_F) вычислена, таблица приведена в [2]). То же самое можно сказать и о дроби, стоящей в конце выражения. При таких предположениях уравнение, которое называют уравнением Фаулера-Нордгейма, имеет следующую форму:

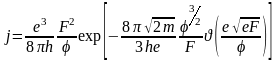(3.1.41)

Подставляя численные значения констант и выражая j в А/см², F в В/см,  в эВ имеем:

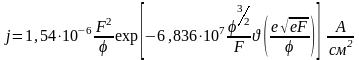(3.1.42)

Из полученного выражения следует, что должна быть сильная зависимость тока от напряженности электрического поля. Как и в случае термоэмиссии, предэкспоненциальный множитель не оказывает существенного воздействия на характер зависимости. Основное влияние оказывает показатель экспоненты. В координатах ln(j/F²) от 1/F должна наблюдаться прямолинейная зависимость. Кроме того, весьма существенна и величина работы выхода острия, которая также входит в показатель экспоненты.

Зависимость автоэмиссиионного тока от температуры незначительна. В явном виде ее можно получить, если воспользоваться (3.1.40). При низких температурах аргумент синуса мал, что позволяет воспользоваться разложением в ряд:

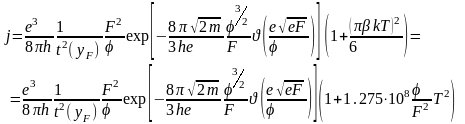(3.1.44)

Видно, что от температуры (при не очень высоких Т) автоэмиссионный ток зависит слабо. Причем эта зависимость тем слабее, чем выше напряженность электрического поля. Например, в случае вольфрама (=4.5 эВ) увеличение Т до 1000 К приводит к возрастанию тока всего лишь в 2.5 раза при F=210⁷ В/см и в 1,7 раз при F=310⁷ В/см. Это ожидаемый результат, поскольку в случае металла при повышении температуры происходят не очень существенные изменения в распределении электронов по энергиям в области, примыкающей к уровню Ферми. На рис.3.1.5 приведен ряд зависимостей, рассчитанных с использованием уравнения (3.1.45). Однако, нужно иметь ввиду, что приведенное выражение справедливо лишь в низкотемпературной области. При повышенных температурах необходимо учитывать наряду с автоэлектронной эмиссией также и термоэлектронную. Это так называемая область термоавтоэлектронной эмиссии, для описания которой должны использоваться уже другие выражения.