4. Преломление лучей сферической поверхностью

П усть две однородные прозрачные среды с показателями преломления п₁ и п₂ разделены сферической поверхностью, радиус кривизны которой R. Проведем оптическую ось через точки А₁, А₂ и центр кривизны сферической поверхности С (рис. 1.11).

Получим формулу для определения положения точки А₂, являющейся изображением точки А₁. При этом будем рассматривать только лучи, составляющие с оптической осью столь малые углы, что практически можно считать, что и . Такие лучи называют параксиальными.

При этом учтем правила знаков. Пусть луч А₁М падает на сферическую поверхность под углом i. Сопряженный ему луч МА₂ (угол преломления r) пересечет оптическую ось в некоторой точке А₂. Обозначим А₁О = -а₁; А₂О = +а₂; ОС = R (радиус сферы).

Из треугольников МА₁С и СМА₂ по теореме синусов имеем:

,

или

.

После несложных преобразований приведем последнее выражение к виду:

. (1.9)

Из (1.9) видно, что преломлении на сферической поверхности произведение не изменяет своей величины Q. Выражение (1.9) называют параксиальным (нулевым) инвариантом Аббе (немецкий физик-оптик). Представленное в виде

, (1.10)

выражение называется уравнением параксиального (нулевого луча).

При малых углах и все лучи, исходящие из точечного объекта А₁, после преломления пересекаются в точке А₂. Для параксиальных лучей гомоцентрический пучок после преломления на сферической поверхности остается гомоцентрическим пучком и точка А₂ является стигматическим изображением точки А₁.

Ограничиваясь рассмотрением параксиальных лучей, определим точку, через которую пройдут после преломления на сферической поверхности все лучи, которые можно выделить в параллельном пучке. Для этого в формуле (1.10) нужно предположить а₁ = . С учетом этого условия получим заднее фокусное расстояние:

. (1.11)

Если а₂ , найдем переднее фокусное расстояние:

. (1.12)

Точки, в которых пересекаются после преломления лучи, падающие на сферическую поверхность параллельным пучком, называются передним (F₁) и задним (F₂) фокусами.

Сравнивая формулы (1.11) и (1.12), можно найти соотношения между фокусными расстояниями:

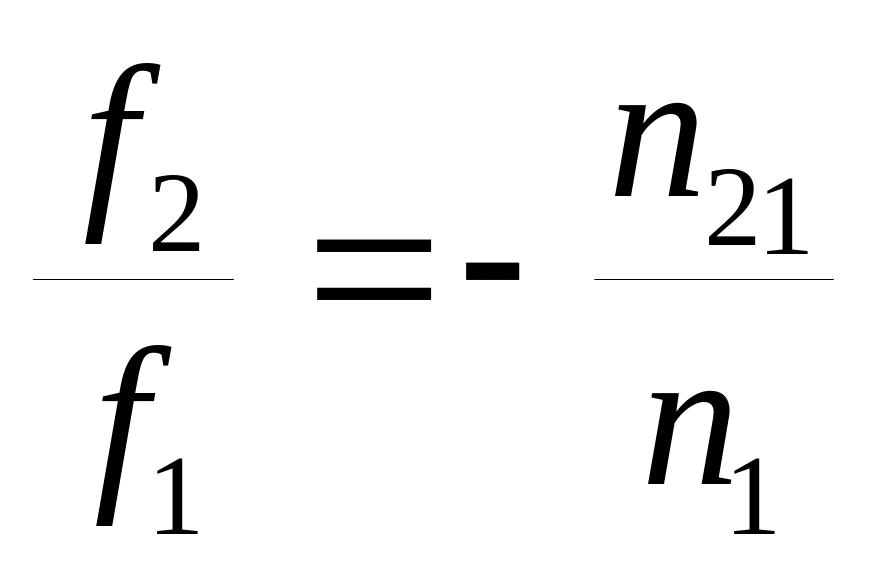. (1.13)

Из формулы (1.13) ясно, что фокусные расстояния пропорциональны показателям преломления сред, в которых лежат фокусы. Знак минус в правой части выражения (1.13) указывает на то, что переднее и заднее фокусное расстояния имеют разные знаки, то есть они лежат по разные стороны преломляющей поверхности.

Преобразуя совместно уравнение параксиального (нулевого) луча (1.10) и уравнения (1.11), (1.12), можно получить формулу

. (1.14)

Если отсчитать отрезки, определяющие положение точек А₁ и А₂ от переднего и заднего фокуса соответственно и обозначить эти отрезки через х₁ и х₂, то получим:

, .

Подставляя эти выражения в (1.14), получим формулу Ньютона:

. (1.15)

Применяя полученные результаты для сферического зеркала (п₂=-п₁), получим формулу сферического зеркала:

. (1.16)

Фокусное расстояние сферического зеркала F = R/2. Фокус вогнутого зеркала действительный, фокус выпуклого зеркала мнимый. Для плоского зеркала , и , то есть изображение точки в плоском зеркале мнимое и расположенное симметрично объекту относительно поверхности зеркала.