3. Принцип Ферма

В оптически однородной среде, то есть в среде, которая во всех точках характеризуется одним и тем же значением показателя преломления, свет распространяется по такому пути, время распространения по которому от одной точки до другой меньше времени распространения его между этими же точками по любому другому пути. Это утверждение называют принципом Ферма в честь французского физика и математика Пьера Ферма, сформулировавшего это положение в 1660 г. Этот принцип справедлив для лучей, отражающихся и преломляющихся на плоских поверхностях. Показано, что формулировке Ферма этот принцип не всегда выполняется для лучей, преломляющихся и отражающихся от изогнутых поверхностей. В современной формулировке принцип Ферма гласит: свет распространяется по пути, оптическая длина которого экстремальна, то есть она является минимальной из всех возможных, максимальной из всех возможных или стационарной. При этом под оптической длиной пути понимают расстояние, которое свет прошел бы в вакууме за то же время, за которое он прошел в среде (средах) между двумя заданными точками. Иначе оптический путь называют приведенной длиной пути. В однородной среде оптическая длина пути равна произведению показателя преломления среды на геометрическую длину пути, пройденного светом в этой среде:

. (1.2)

Если среда неоднородна, геометрический путь нужно разбить на такие малые отрезки ds, чтобы на протяжении каждого из них можно было считать показатель преломления постоянным. Тогда элементом оптической длины пути будет величина dl=nds, а вся оптическая длина пути между точками А и В будет равна

. (1.3)

Условие экстремальности оптической длины пути сводится к требованию, чтобы первая вариация от интеграла равнялась нулю:

. (1.4)

Рассмотрим частные ситуации, в которых принцип Фермы выполняется.

Для однородной среды из этого принципа следует закон прямолинейного распространения света, в соответствии с геометрической теоремой о том, что отрезок прямой есть кратчайшее расстояние между двумя точками. Воспользовавшись этим принципом, можно доказать закон преломления света (рис. 1.9).

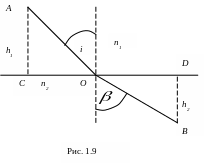
Пусть луч АОВ преломляется в точке О, положение которой на прямой CD=p определяется отрезком СО=х. Для пары точек А и В длина отрезка р постоянна.

Оптическая длина пути вдоль луча АОВ равна

. (1.5)

После определения длины отрезков АО и ОВ получим:

. (1.6)

Условие экстремальности оптического пути заключается в том, что . Дифференцируя (2.6), получим:

. (1.7)

Из рисунка 1.9 ясно, что

; . (1.8)

Тогда из выражения (1.7) получим:

,

то есть путь, удовлетворяющий условию экстремальности, удовлетворяет и закону преломления.

Аналогичным образом можно доказать закон отражения света.

Ситуации, в которой реализуется стационарность оптического пути, реализуется при отражении света от вогнутой зеркальной поверхности, имеющей форму эллипсоида вращения (рис. 1.10).

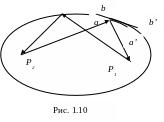
Если свет исходит из точки Р₁, являющейся фокусом эллипсоида, то при отражении в любой точке О зеркала он попадает во второй фокус эллипсоида Р₂. Из известного свойства эллипсоида, что сумма Р₁О + ОР₂ есть постоянная величина для всех положений точки О на поверхности эллипсоида, следует, что длина пути Р₁ОР₂ равна длине любого другого пути Р₁О’Р₂. Если провести две вогнутые поверхности аа’ и bb’, касательные к поверхности эллипсоида, то длина пути уже не будет стационарной при отражении от таких поверхностей в точке O и точке O', лежащей на одной из этих поверхностей. Однако условие экстремальности будет выполняться: если кривизна поверхности bb’ меньше кривизны поверхности эллипсоида, оптический путь Р₁ОР₂ меньше, чем Р₁О’Р₂. Если кривизна поверхности аа’ больше кривизны поверхности эллипсоида, то оптический путь Р₁ОР₂ оказывается максимальным.