§ 3. Тригонометрические ряды. Ряды Фурье. Основные понятия. Разложение в ряд Фурье функций с периодом 2.

Определение 7. Функциональный ряд вида:

+ ( a_ncos nx + b_nsin nx ) (1)

называется тригонометрическим, причем a_n и b_n – действительные числа, не зависящие от x.

Пусть y = f(x) – произвольная периодическая функция с периодом Т = 2, следовательно, функцию можно рассматривать в любом интервале длины 2, например, (–; ). На других участках оси (Ох) функция f(x) и ее разложение в ряд будет повторять свои значения и свое поведение в основном интервале.

Предположим, что для любого x(–; ) периодическая функция оказалась такой, что для нее нашлось разложение в равномерно сходящийся ряд указанного вида:

f(x) = + ( a_kcos kx + b_ksin kx ) ( 1.1)

Такое представление дает возможность находить численные значения функции, устанавливать различные свойства функций, решать дифференциальные уравнения и т.п.

Получим формулы для вычисления коэффициентов a_k и b_k. Проинтегрируем почленно данное равенство в пределах от – π до π (законное в силу предложенной сходимости):

. (1.2)

Вычислим отдельно следующие интегралы:

если n – целое,

(1.3)

(1.4)

если n, m – целые, положительные

(1.5)

= (1.6)

. (1.7)

С учетом формул (1.3) и (1.4) почленное интегрирование равенства (1.2) дает:

(1.8)

Умножая (1.1) на cos nx и интегрируя почленно от – π до π, с учетом (1.3), (1.5), (1.7), получим:

(1.9)

Аналогично, умножая (1.1) на sin nx и интегрируя почленно от – π до π и учитывая (1.4), (1.6), (1.7), получим:

(1.10)

Таким образом, из равенств (1.8), (1.9), (1.10) получим выражения для нахождения коэффициентов.

Теорема 1. Если функция f(x), заданная и непрерывная на отрезке [-; ], разлагается в тригонометрический ряд, то коэффициенты его определяются единственным образом.

Определение 8. Пусть f(x) – произвольная функция с периодом 2, заданная в интервале (–; ). Пусть существует интеграл от данной функции в интервале (–; ), при этом f(x) может иметь конечное число точек разрыва 1-го рода. Рядом Фурье этой функции называется ряд

+

коэффициенты которого определяются по формулам:

а₀ = ; ( 1.11)

а_n = (n =1,2,...); ( 1.12 )

b_n = (n =1,2,...). ( 1.13 )

Замечание 1. Для вычисления интегралов потребуются следующие формулы:

для любого n, , , ,

Из определения ряда Фурье не следует, что функция должна в него разлагаться. Из сказанного выше следует следующая теорема:

Теорема 2 (единственности). Если непрерывная на [-; ] функция разлагается в равномерно сходящийся тригонометрический ряд, то этот ряд будет обязательно ее рядом Фурье.

Замечание 2. Исходя из теоремы, в определении можно рассматривать не интервал (–; ), а отрезок [–; ].

Функция f(x) не всегда разлагается в свой ряд Фурье, т.е. является его сумой, даже если он сходится, а лишь тогда, когда она удовлетворяет условиям основной теоремы:

Теорема 3 (основная). Если функция f(x) кусочно-гладкая на отрезке [-; ], то ее ряд Фурье сходится к функции f(x) во всех точках, в которых она непрерывна. В точках разрыва функции f(x) ряд сходится к среднему арифметическому ее предельных значений слева и справа, т.е. к значению , где – точка разрыва 1-го рода. В обеих граничных точках интервала сумма ряда равна среднему арифметическому предельных значений функции при стремлении независимой переменной к этим точках изнутри интервала (без доказательства).

Замечание. Функция называется гладкой в интервале, если в этом интервале она непрерывна вместе со своей первой производной. Функция называется кусочно-гладкой в интервале, если данный интервал можно разбить точками разрыва 1-го рода на конечное число интервалов, в каждом из которых функция гладкая.

Следствие теоремы.

Теорема гарантирует разложимость всякой дифференцируемой на отрезке [–; ] функции в ее ряд Фурье не на всем этом отрезке, а лишь на открытом промежутке (–; ), однако если разлагаемая функция удовлетворяет еще дополнительному условию, что , то она будет представима своим рядом Фурье на всем отрезке [–; ].

Существуют и иные достаточные признаки разложимости функций в ряд Фурье, например, следующая теорема:

Теорема 4 (Дирихле).

Если функция f(x) имеет на интервале (-; ) лишь конечное число максимумов и минимумов и непрерывна, за исключением, м.б., конечного числа точек разрыва 1-го рода, то f(x) разлагается в ряд Фурье, сходящийся в точках непрерывности к самой функции, а в точках ее разрыва – к значению . (без доказательства)

В силу основной теоремы, если ряд является рядом Фурье функции f(x), можно написать:

f(x) = + ( a_ncos nx + b _nsin nx ) ( 1.14 )

Пример 1: Разложить в ряд Фурье функцию с периодом 2:

f(x) =

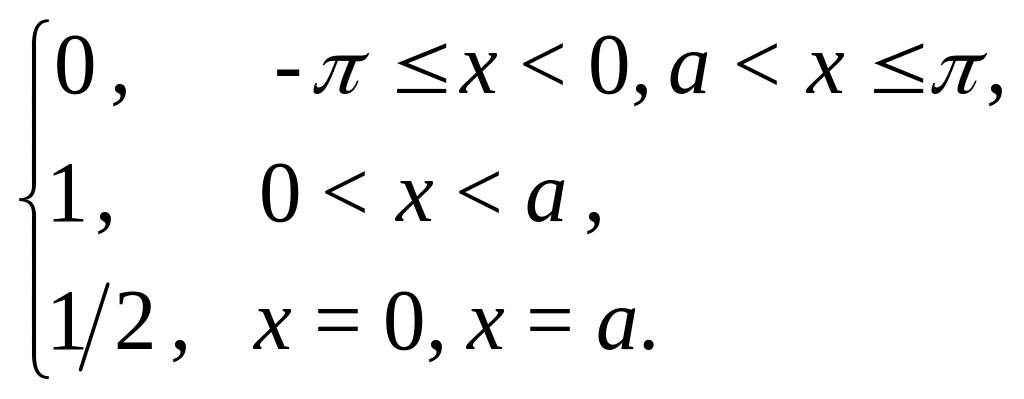
Решение:

Из определения f(x) следует, что она удовлетворяет условиям теоремы о разложимости в ряд Фурье, поэтому f(x) разлагается в ряд Фурье. (См. рис. 1.)

Рис. 1.

По формулам (1.11)-(1.13) находим коэффициенты Фурье:

а₀ = = = 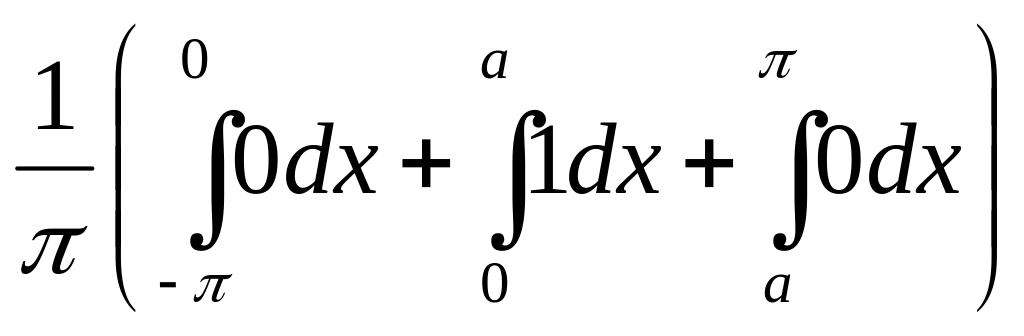= а/.

а_n = = = = 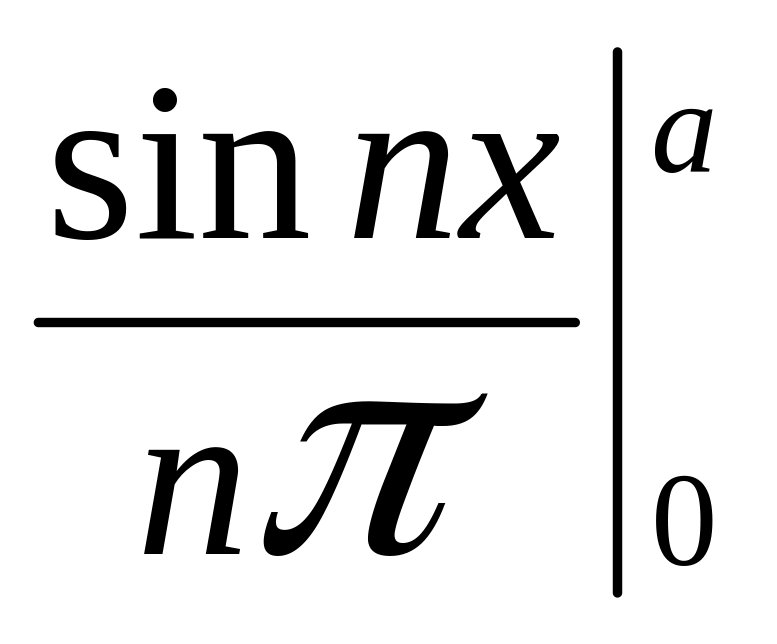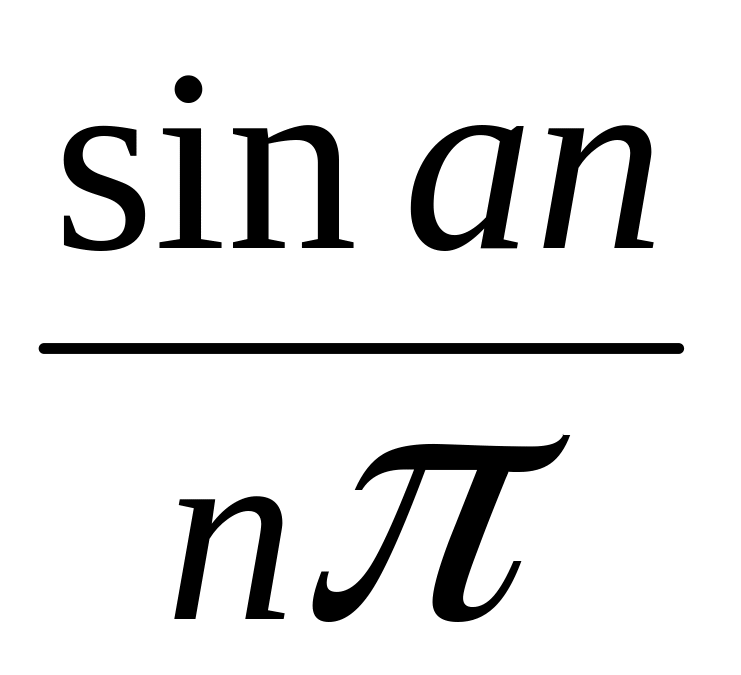, при n  0.

Замечание.

Если n = 0, то для вычисления а_n поступаем следующим образом: рассмотрим предел при n0

= = = ,

b_n = = = – = –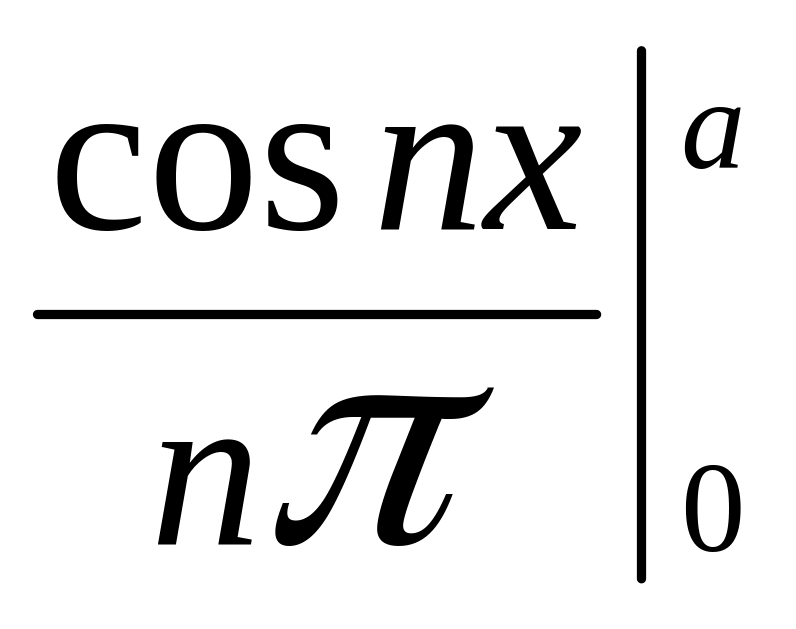 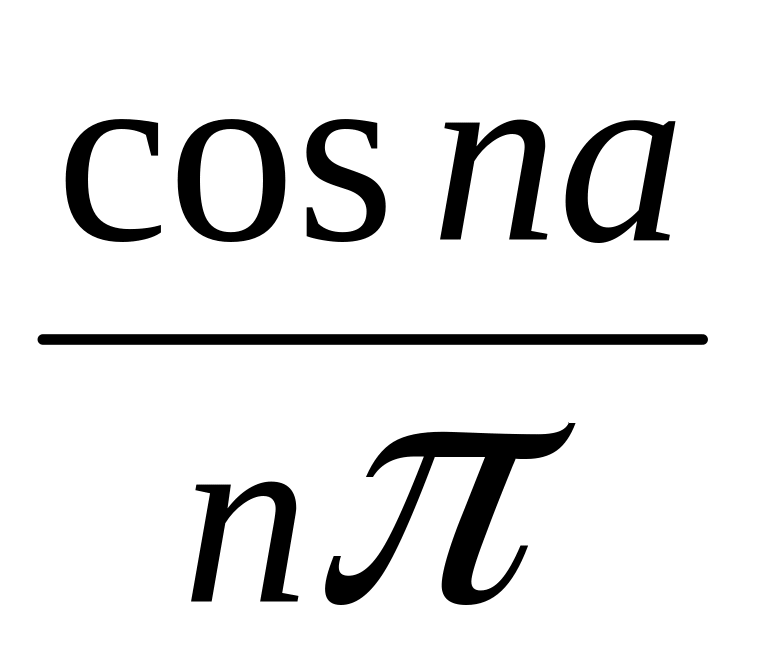+ = 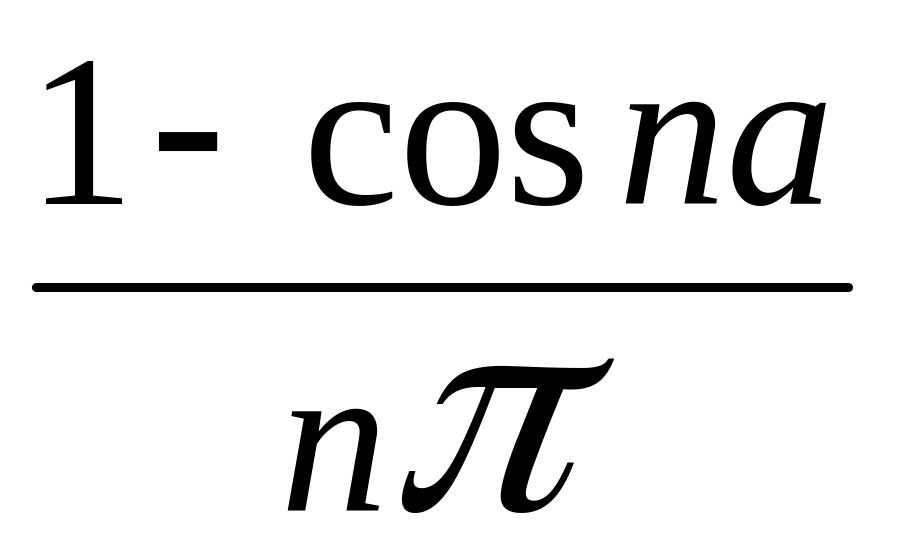, при n  0.

Следовательно,

f(x) = .

В интервале [-; ] ряд сходится к функции f(x), в точках х =   к 0: ( 1/2 [ f(–+0) + f(–0)] = 0 ), в точках х = a, x = 0 к 1/2 : ( 1/2 [ f(х-0) + f(х+0)] = =1/2 ).