Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Математический анализ

Файл:

Математический анализ определенный интеграл, несобственный интеграл, приложения определенного интеграла

.pdf

Скачиваний:

124

Добавлен:

01.05.2014

Размер:

3.1 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

по значку k от 0 до n −1, получим, что площадь S всего обобщенного сектора будет удовлетворять неравенству

n−1	n−1	12 Mk2 ∆ϕk .
∑	12 mk2 ∆ϕk ≤ S ≤ ∑	12 Mk2 ∆ϕk .	(8)
k =0	k=0

n−1	12 mk2 ∆ϕk	n−1	12 Mk2 ∆ϕk , являясь нижней и верх-
Заметим, что суммы ∑	12 mk2 ∆ϕk	и ∑	12 Mk2 ∆ϕk , являясь нижней и верх-
k =0		k =0

ней суммами Дарбу соответственно, являются также интегральными суммами Римана для функции 12 f 2 (ϕ) в промежутке [α,β]. Так как f (ϕ) C([α,β]), то

1		2	(	)	1	f 2	(	)
1	f	2	(ϕ) C [α,β]		1	f 2	(ϕ) R [α,β]		lim σ существует и равен
2					2				λ→0
β	12
∫	12	f 2 (ϕ) dϕ. Переходя в неравенстве (8) к пределу при λ → 0 , получим
α

β	12 f 2 (ϕ) dϕ.
S = ∫	12 f 2 (ϕ) dϕ.	(9)
α

Замечание 1. Пусть фигура ограни-

ϕ=β

r = f2 (ϕ)

чена линиями, уравнения которых в по-

лярной системе координат имеют вид

ϕ = α,

ϕ = β

( α < β),

r = f1(ϕ) , O

r = f

(ϕ)

ϕ [α,β],

r = f2 (ϕ) ,

ϕ [α,β]

(рис.

3.12).

При

этом

предполагается,

что

ϕ=α

f (ϕ), f

(ϕ) C [α,β] ,

f (ϕ) ≤ f

(ϕ) ,

Рис. 3.12. К выводу формулы (10) для

(

)

ϕ [α,β].

Обозначим через S площадь площади разности двух обобщенных сек-

фигуры ABCD. Будем иметь

торов

[f22 (ϕ) − f12 (ϕ)]dϕ. (10)

S = SODC − SOAB = 12 ∫ f22 (ϕ) dϕ− 12 ∫ f12 (ϕ) dϕ = 12 ∫

Замечание 2. Отрезки лучей ϕ = α, ϕ = β (один или оба сразу) могут выро-

ждаться в точку.

Пример

Найти

площадь части

фигуры,

ограниченной

линией

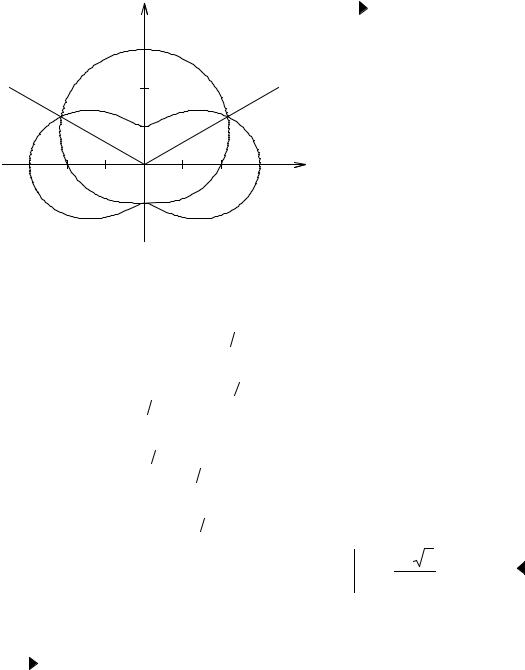
r = 2 + cos 2ϕ, лежащей вне линии r = 2 +sin ϕ (рис. 3.13).

111

					y																				Лучи,					соответствующие точкам
						3															пересечения									линий,				находим,								решая
						3															уравнение
		5																π			уравнение
		5																π					2 + cos 2ϕ = 2 +sin ϕ ϕ = π
ϕ=		6 π				2												ϕ= 6					2 + cos 2ϕ = 2 +sin ϕ ϕ = π																				,
						2																																		1		6
																											= 5						3									6
						1																		ϕ		2	= 5		π	, ϕ	3	=	3	π		( ϕ		3	= − π ).
			−2			1						2						x ( p)								2		6			3		2					3		2
																		x ( p)					Положим
−3				−1		0												3					Положим
−3				−1		0				1								3					f1(ϕ) = 2 +sin ϕ ,										f2 (ϕ) = 2 + cos 2ϕ.
																					Воспользовавшись												симметрией									фигу-
																					ры относительно оси Oy, можно рас-
Рис. 3.13. К вычислению площади фигуры																					сматривать									ϕ − π,						π .				Так			как
					в примере 3																												2
					в примере 3																												2			6
																						f1(ϕ) ≤ f2 (ϕ)												π	,		π		, то
																						f1(ϕ) ≤ f2 (ϕ)								, ϕ −				2	,		6		, то
														π 6																				2			6
							S = 2 12							π 6
							S = 2 12							∫[(2 +cos 2ϕ)2 −(2 +sin ϕ)2 ]dϕ =
													−π 2
					π 6												1+cos 4ϕ											1−cos 2ϕ
					=	∫		4 cos 2ϕ +										2			−4sin ϕ −									2		dϕ =
					−π 2													2												2
									=		π 6			9		cos 2ϕ +			1
									=		∫			2		cos 2ϕ +			2	cos 4ϕ −4sin ϕ dϕ =
											∫			2					2
											−π 2
						9							1										π				51		3
						9	sin 2ϕ +						1		sin								6		=		51		3	(кв. ед.).
					=	4	sin 2ϕ +						8		sin			4ϕ +4 cos ϕ						π	=			16		(кв. ед.).
						4							8										−	π				16
																							−	2
																								2
		Пример 4. Найти площадь общей части фигур, ограниченных линиями
r = 3 + cos 4ϕ и r = 2 − cos 4ϕ (рис. 3.14).
		Лучи, соответствующие точкам пересечения линий, находим, решая урав-
нение			3 + cos 4ϕ = 2 − cos 4ϕ													cos 4ϕ = − 1													ϕ =			π	,	ϕ	2		=	π ,		ϕ	3	=	2 π,
																							2							1		6			2			3			3		3
ϕ	4	= 5	π , ϕ	5	= 7 π, ϕ				6		= 4	π		, ϕ			7	= 5 π,		ϕ	8	=	11		π.
	4	6		5	6				6		3						7	3			8		6

Для нахождения искомой площади S воспользуемся симметрией фигуры относительно координатных осей и биссектрис координатных углов. Будем иметь

~	~
S = 8S , где S – площадь заштрихованной фигуры. Заштрихованная фигура со-
стоит из двух обобщенных секторов. Первый ограничен линиями: ϕ = 0		, ϕ = π	,
		6

112

r = 2 − cos 4ϕ,	ϕ					π		. Второй ограничен	линиями: ϕ =		π	,	ϕ =	π	,
r = 2 − cos 4ϕ,	ϕ		0,			6		. Второй ограничен	линиями: ϕ =		6	,	ϕ =	4	,
						6					6			4
r = 3 + cos 4ϕ,	ϕ	π		,	π		. Имеем, следовательно,
r = 3 + cos 4ϕ,	ϕ	6		,	4		. Имеем, следовательно,
		6			4			y
								y		π
								4	ϕ =	π
									ϕ =	4
									r = 3 +cos 4ϕ
									ϕ =	π
										6
									r = 2 −cos 4ϕ
								0	x ( p)
								0	4

Рис. 3.14. К вычислению площади фигуры в примере 4

π 6

π 4

= 8

∫

(2 −cos 4ϕ)

dϕ +

∫

(3 + cos 4ϕ)

dϕ

π −5

(кв. ед.).

S = 8S

π 6

§2. Вычисление длины кривой

Приступим к выяснению понятия длины кривой линии. Предварительно заметим, что на кривой обычно различают два взаимно противоположных направления, из которых одно считают положительным, другое – отрицательным. Например, в случае параметрического задания кривой считают, что положительное направление отвечает возрастанию параметра, отрицательное – убыванию параметра.

Отметим далее, что если на кривой даны несколько точек, и порядок их следования совпадает с определенным направлением на кривой, то в отношении этих точек говорят, что они следуют друг за другом вдоль кривой.

Итак, пусть имеется кривая (AB (точки A и B – концы этой кривой). Возьмем на (AB ряд точек, следующих друг за другом вдоль кривой: M0 = A , M1 ,

K , Mn−1 , Mn = B (равенства для точек, вроде M0 = A , Mn = B , означают попросту, что соответствующие точки совпадают). Соединяя последовательно эти

113

Mn−1

M2 B =Mn

A=M0

Рис. 3.15. Ломаная, вписанная в дугу кривой

точки прямолинейными отрезками, получим


некоторую			ломаную линию, вписанную в
(AB (рис.			3.15). Обозначим через				Mk Mk+1
(AB (рис.			3.15). Обозначим через				Mk Mk+1
длину		k-го		звена		ломаной.	Тогда
	n−1
lлом. = ∑		Mk Mk+1			будет	длиной всей лома-
lлом. = ∑		Mk Mk+1			будет	длиной всей лома-

k=0

ной.

Заметим, что для закрепленного числа n и для закрепленного способа выбора точек M1, M2 , K, Mn−1 значение величины lлом.

будет вполне определенным числом. Если же число точек M1, M2 , K, Mn−1 и способы их выбора на (AB менять, то будет

изменяться, вообще говоря, значение величины lлом. .

Положим λ = max Mk Mk+1 .

k=0, n−1

Определение. Если существует конечный предел длины вписанной в дугу ломаной

l = lim lлом. ,	(1)
λ→0

не зависящий от способа выбора вершин ломаной, то этот предел называют длиной (AB , а саму (AB называют в этом случае спрямляемой.

1°. Длина дуги кривой, заданной параметрически.

Теорема 1. Пусть (AB задана параметрически уравнениями

x = ϕ(t),	t [α,β] (α <β) .
	t [α,β] (α <β) .
y = ψ(t),

(Считаем (AB незамкнутой и не имеющей кратных точек; каждая точка на (AB получается лишь при одном значении параметра t .) Пусть функции ϕ(t),

ψ(t) имеют в промежутке [α,β] непрерывные производные ϕ′(t) , ψ′(t) . Тогда (AB спрямляема, и ее длину следует вычислять по формуле

β
l = ∫ [ϕ′(t)]2 +[ψ′(t)]2 dt .	(2)
α
Впишем в (AB ломаную M0 M1KMn ( M0 = A ,	Mn = B ), причем сдела-
ем это так: разделим промежуток [α,β] точками α = t0 < t1 <K< tn = β произ-


вольным образом на части [tk , tk+1] ( k =				),	и возьмем в качестве точек
вольным образом на части [tk , tk+1] ( k =			0, n −1	),	и возьмем в качестве точек
Mk ( xk , yk ) на (AB точки, у которых xk = ϕ(tk ) ,					yk = ψ(tk ) (рис. 3.16). Длина
k-го звена ломаной	Mk Mk+1	будет равна
k-го звена ломаной	Mk Mk+1	будет равна

Mk Mk+1 = (xk+1 − xk )2 +( yk+1 − yk )2 .

114

Но xk+1 − xk = ϕ(tk+1 ) −ϕ(tk ), yk+1 − yk = ψ(tk+1 ) − ψ(tk ) . Поэтому

Mk Mk+1 = (ϕ(tk+1 ) −ϕ(tk ))2 +(ψ

Замечаем, что функции ϕ(t), ψ(t) в промежутке [tk , tk+1] удовлетворяют условиям тео-

ремы Лагранжа. Следовательно, можем написать:

ϕ(tk+1 ) −ϕ(tk ) = ϕ′(τk ) ∆tk , точка τk [tk , tk+1],

ψ(tk+1) −ψ(tk ) = ψ′(θk ) ∆tk , точка θk [tk ,tk+1].

Тогда Mk Mk+1 = [ϕ′(τk )]2 +[ψ′(θk )]2 ∆tk , k = 0, n −1. Для длины всей ломаной будем иметь

(tk+1 ) − ψ(tk ))2 .

B =Mn

Mn−1

A=M0

Рис. 3.16. К выводу формулы для длины дуги

n−1
lлом. = ∑ [ϕ′(τk )]2 +[ψ′(θk )]2 ∆tk .	(3)

k=0

Замечаем, что сумма (3) очень похожа на интегральную сумму Римана для интеграла, стоящего в правой части (2), но таковой не является, ибо, вообще гово-

ря, θk ≠ τk .

Введем в рассмотрение сумму

n−1
σ = ∑ [ϕ′(τk )]2 +[ψ′(τk )]2 ∆tk .	(4)

k =0

Это уже настоящая интегральная сумма Римана для интеграла (2). У нас по ус-

(

)

[

]

[

]

(

)

ловию

ϕ′(t), ψ′(t) C [a, b]

ϕ′(t)

2 +

ψ′(t) 2

C [a, b]

[

]

[

]

(

)

существует и

равен

ϕ′(t) 2

ψ′(t) 2

R [a, b]

lim

λ→0

max

∫

[ϕ′(t)] +

[ψ′(t)] dt

( λ =

{∆tk }).

k =0, n−1

Заметим,

что

( λ → 0 )

(это

доказано,

например,

книге

( λ → 0)

Г.М. Фихтенгольца «Курс дифференциального и интегрального исчисления»,

т. I, с. 557).

Рассмотрим очевидное равенство

lлом. = σ +(lлом. −σ) .			(5)
Из (5) видно, что теорема будет доказана, если показать, что
lim (l	лом.	−σ) = 0 .	(6)
~	лом.
λ→0

Имеем

115

лом.

n−1

[

−σ =

∑

ϕ′(τ

]

ψ′(θ

]

−

ϕ′(τ

]

ψ′(τ

k ]

)

∆t

Отсюда

k=0

n−1

lлом. −σ

≤ ∑

[ϕ′(τk )]2 +[ψ′(θk )]2 −

[ϕ′(τk )]2 +[ψ′(τk )]2

∆tk .

k=0

Так как

N −

≤

, где M и N – любые две неотрицательные вели-

N − M

чины, то получаем

n−1

lлом. −σ

≤ ∑

[ψ′(θk )]2 −[ψ′(τk )]2

∆tk .

(Неравенство

N −

≤

k=0

доказано ниже. См. (7).)

N − M

(

)

[

]

(

)

По условию, ψ′(t) C [a, b]

ψ′(t) 2

C [a, b]

по теореме Кантора:

любому ε > 0

отвечает δ > 0 , зависящее только от ε, такое, что для любых двух

точек

t′,

t′′

из

[α,β]

для

которых

t′′ −t′

< δ,

будет

ε2

[ψ′(t′′)]

−[ψ′(t′)]

. Возьмем дробление промежутка [α,β]

на части

(β−α)2

[tk , tk+1]

любое,

но

такое,

чтобы

было

Тогда

для

всех k = 0, n −1:

λ < δ.

θk − τk

и,

следовательно,

сразу

для

всех

k = 0, n −1:

≤ λ < δ

ε2

[ψ′(θk )]

−[ψ′(τk )]

. Тогда будем иметь:

(β−α)2

n−1

lлом. −σ

∑∆tk

= ε.

β−α

		k=0
Неравенство	lлом. −σ	~
		~
		< ε получено нами лишь в предположении, что λ < δ. Это

означает, что lim (lлом. −σ) = 0 .

λ→0

Лемма (неравенство для квадратных радикалов). Пусть M и N – любые две неотрицательные величины. Тогда

N − M ≤

N − M

(7)

В самом деле, пусть A = min

{

M, N

}

{

M, N

}

B = A + h , где

B = max

h ≥ 0 . Тогда (7) запишется в виде

−

≤

A + h

A + h ≤ A + h + 2

≥ 0 .

2°. Длина дуги кривой, заданной явным уравнением.

Теорема 2. Пусть (AB задана явным уравнением

y = f (x),

x [a, b], a < b.

116

Пусть функция f ( x) имеет в промежутке [a, b]			непрерывную производную
f ′(x) . Тогда (AB спрямляема, и ее длину l следует вычислять по формуле
b
l = ∫ 1+[f ′(x)]2 dx .			(8)
a
Представление (AB кривой явным уравнением y = f (x) , x [a, b], мо-
жет быть рассмотрено как параметрическое:
x = x,	x [a, b],	a	< b
y = f (x),
(в роли параметра выступает x).

Имеем xx′ =1,

yx′ = f ′(x) . Видим, что выполнены условия теоремы 1. Сле-

довательно,

(AB

спрямляема,

и ее длину l

следует вычислять по формуле

l = ∫ 1+[f ′(x)]2 dx .

3°. Длина дуги кривой, заданной уравнением в полярных координатах.

Теорема 3. Пусть

(AB задана уравнением

r = f (ϕ),

ϕ [α,β],

α <β.

Пусть функция f (ϕ)

имеет в промежутке [α,β]

непрерывную производную

f ′(ϕ) . Тогда (AB спрямляема, и ее длину l следует вычислять по формуле

[f (ϕ)]2 +[f ′(ϕ)]2 dϕ.

l = ∫

(9)

Имеет место следующая связь между полярными и декартовыми коорди-

натами точки:

x = r cos ϕ,

y = r sin ϕ.

Следовательно, параметрические уравнения (AB в этом случае будут такими:

x = f (ϕ) cos ϕ,

ϕ [α,β],

α <β

y = f (ϕ) sin ϕ,

(в роли параметра выступает ϕ).

Имеем

x′ =

f ′(ϕ)cos ϕ − f (ϕ)sin ϕ,

[xϕ′ ]2 +[ yϕ′

]2 =[f (ϕ)]

+[f ′(ϕ)]

yϕ′ =

f ′(ϕ)sin ϕ + f (ϕ)cos ϕ,

(AB спрямляема, и ее дли-

Видим, что выполнены условия теоремы 1. Значит,

ну l следует вычислять по формуле

117

l = ∫ [f (ϕ)]2 +[f ′(ϕ)]2 dϕ.

α
Замечание. Если (AB – пространственная		и задана параметрическими
уравнениями
x = ϕ(t),
y = ψ(t),	t [α,β],	α <β,
z = ω(t),

и если функции ϕ(t), ψ(t), ω(t) имеют в промежутке [α,β] непрерывные производные ϕ′(t) , ψ′(t) , ω′(t), то совершенно аналогично устанавливают, что

(AB спрямляема и что ее длину l следует вычислять по формуле

l = ∫ [ϕ′(t)]2 +[ψ′(t)]2 +[ω′(t)]2 dt .

Часто пространственная кривая представляется как линия пересечения двух поверхностей, проектирующих ее на координатные плоскости, т.е. задается сис-

темой
y = f (x),	x [a, b], a < b,
z = g(x),
причем функции f ( x) , g( x) имеют непрерывные производные в промежутке

[a, b] . (Это представление кривой может быть рассмотрено как своего рода па-

раметрическое, что станет видно сразу, если написать:				x = t ,	y = f (t) ,	z = g(t) ,
t [a, b] и a < b .) В этом случае
	b
	l = ∫ 1+[f ′(x)]2 +[g′( x)]2 dx .
	a
Пример 1. Вычислить длину одного витка винтовой линии (рис. 3.17)
	x = a cos t,
			t [0, 2π].
	y = a sin t,		t [0, 2π].

	z = bt,		(x′)2 +	( y′)2 +(z′)2 = a2		+b2 ,
Имеем x′ = −a sin t ,	y′ = a cos t ,	z′ = b	(x′)2 +	( y′)2 +(z′)2 = a2		+b2 ,
t	t	t	t	t	t

2π

l = ∫ a2 +b2 dt = 2πa2 +b2 .

118

z y

1 2

−1

−2

Рис. 3.17. Винтовая линия

Рис. 3.18. К вычислению длины дуги в примере 2

Пример 2. Вычислить длину полукубической параболы

y2 = 23 (x −1)3 ,

за-

ключенной внутри параболы

y2 =

(рис. 3.18).

= 23 ( x −1)3

Найдем абсциссы точек пересечения парабол из уравнения

x = 2 – единственный вещественный корень.

Имеем 2 yy′ = 3 2 (x −1)2

y′ = (x −1)2

( y′ )2

= ( x −1)4

( y′ )2

= ( x −1)4 3

= 3 (x −1)

1+( y′ )2 = 3x −1

Воспользовавшись

2(x −1)3

симметрией относительно оси Ox, можем написать

= 2 92

(5 5

−2 2).

l = 2∫ 3x2−1 dx = 2 92 (3x −1)3 2 1

y
A	x
O
M	C
M

Рис. 3.19. К вычислению длины линии в примере 3

Пример 3. Найти длину линии, заданной уравне-

нием r = a sin			3	ϕ	(рис. 3.19).
нием r = a sin				3	(рис. 3.19).
				3
	ϕ	Считая		r ≥ 0 , получим,		что		должно быть:
sin	ϕ	≥ 0 ϕ [0, 3π].
sin	3	≥ 0 ϕ [0, 3π].				3
	При изменении ϕ от 0 до					3	π	длина радиуса-
						2

вектора r возрастает от 0 до a, а конец радиусвектора описывает дугу OAMB. Затем, при измене-

нии ϕ от 23 π до 3π величина r убывает от a до 0;

119

при этом описывается дуга BCAO, симметричная дуге OAMB относительно прямой ϕ = ± π2 .

Имеем:

rϕ′ = a sin	2	ϕ	cos			ϕ		,			r	2	+(rϕ′)			2	= a		2				6	ϕ		+sin			4	ϕ		cos		2 ϕ		= a	2	sin	4	ϕ	,
rϕ′ = a sin		3	cos			3		,			r		+(rϕ′)				= a			sin				3		+sin				3		cos		3		= a		sin		3	,
		3				3																		3						3				3						3
								r		2	+(rϕ′)			2	= a sin				2	ϕ		=	a				−cos			2ϕ
								r			+(rϕ′)				= a sin					3		=			1		−cos					.
																				3			2								3
Следовательно,					3π
		l =		a					−cos				2ϕ					a			ϕ −			3	sin			2ϕ			3π		3aπ		.
				a									2ϕ					a						3				2ϕ			3π		3aπ
				2	∫		1							dϕ =				2						2								=		2
				2	∫								3					2						2				3			0			2
					0

4°. Переменная дуга и ее дифференциал. Пусть (AB кривой задана пара-

метрическими уравнениями

Рис. 3.20. Переменная дуга

(AM

x = x(t),	t [α,β], α <β.
	t [α,β], α <β.
y = y(t),
Пусть функции x(t) ,	y(t) имеют в промежутке

[α,β] непрерывные производные xt′, yt′.

Возьмем на (AB произвольную точку M. Пусть t есть значение параметра, соответствующее положению точки M на (AB (рис. 3.20). Тогда длина

(AM равна ∫ (xt′)2 +( yt′)2 dt . Ясно, что эта вели-

чина представляет собой некоторую функцию от t, определенную в промежутке [α,β]. Будем обозна-

чать эту функцию через l(t) . Таким образом,

			t
		l(t) = ∫		(xt′)2 +( yt′)2 dt,			t [α,β].				(10)
		t	α	(	)		t	t	(	)
		t	t	(	)		t	t	(	)
У нас, по условию, x′,			y′	C [α,β]			(x′)2	+( y′)2	C [α,β]		для
любого t [α,β] существует l′(t), причем
				l′(t) =	(x	′)2 +( y′)2					(11)
(	)				t		t
(	)	, и l(t) – монотонно возрастающая в [α,β].
l(t) C [α,β]		, и l(t) – монотонно возрастающая в [α,β].
Умножим обе части (11) на dt . Получим
l′(t) dt =		( x′ dt)2 +( y′ dt)2			dl(t) = (dx)2 +(dy)2 ,					t [α,β].
		t	t

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

Соседние файлы в предмете Математический анализ

#
01.05.20142.79 Mб94 семестр (СРВМ).tif
#
01.05.201472.7 Кб35Двойной интеграл.DOC
#
01.05.201444.03 Кб49Еще одна шпора по матану.doc
#
01.05.2014458.74 Кб55Индивидуальное задание 1 по спецглавам матана.mcd
#
01.05.20141.3 Mб51Кратные интегралы.doc
#
01.05.20143.1 Mб124Математический анализ определенный интеграл, несобственный интеграл, приложения определенного интеграла.pdf
#
01.05.20142.6 Mб42Математический анализтеория рядов.pdf
#
01.05.2014617.98 Кб24Производная.doc
#
01.05.201492.67 Кб60Решение типовика по пределам.doc
#
01.05.201497.07 Кб18Специальные главы Матана.mcd
#
01.05.2014129.54 Кб157Шпаргалка на ряды и разные интегралы.DOC