5. Примеры построения математических моделей колебаний для систем со многими степенями свободы

Рассмотрим математические модели колебаний, составленные с использованием уравнений Лагранжа II рода или принципа Д'Аламбера. Будем считать, что связи в рассматриваемых системах имеют упругое сопротивление и неупругое -соответственно пружины и демпферы, реализующие силы сухого и вязкого трения. Построим математические модели для анализа вынужденных колебаний, что позволяет полнее оценить динамическое воздействие на систему, возникновение опасных ситуаций, безопасность движения. Если система не имеет каких-либо диссипаций энергии, отсутствует гаситель колебаний, то из общей модели можно получить более простые системы.

5.1. Построение математических моделей колебаний для систем с двумя степенями

Представим расчетную схему механической системы в виде рис. 5.1. Два тела совершают колебательные процессы при наличии демпферов, реализующих силы сухого и вязкого трения. Генерирование колебаний происходит за счет воздействия на тела со стороны пути, имеющем неровности.

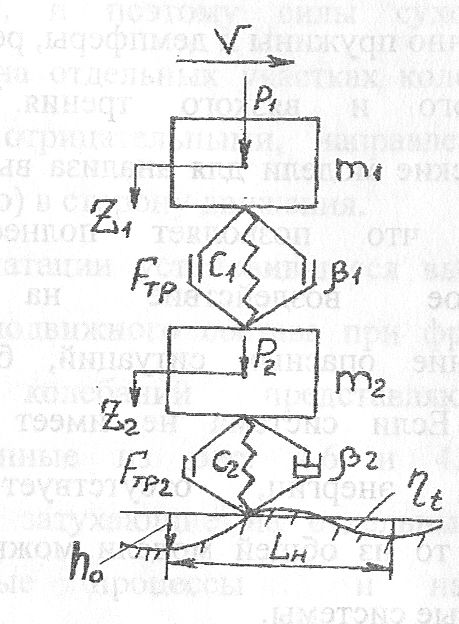
Рис. 5,1 Расчетная схема системы с двумя степенями свободы

Вначале рассмотрим верхний груз. Если ему дать малую деформацию вниз, то возникнет реакция в связи со вторым грузом, направленная вверх. Аналогично для второго груза будет действовать одна реакция со стороны первого груза и вторая - со стороны рельсового пути, имеющего неровности -амплитуда неровности (возмущающей функции); - частота возмущающей функции; 1_н - длина неровности

Рис 5.2 Силовые схемы двухстепенной системы

Рассмотрим силы, действующие на первый груз: силы инерции Р_ин1= -m_lz_l, Р₁- сила тяжести (вес)

(5.1)

реакция в связи между первым и вторым грузами.

Тогда дифференциальное уравнение, описывающее колебания верхнего груза будет иметь вид

(5.2)

Аналогично для нижнего груза:

(5.3)

Тогда дифференциальное уравнение, описывающее колебания второго груза будет иметь вид

(5.4)

или после подстановки в (5.4) значений (5.3) и (5.1) и приведения подобных членов, получим

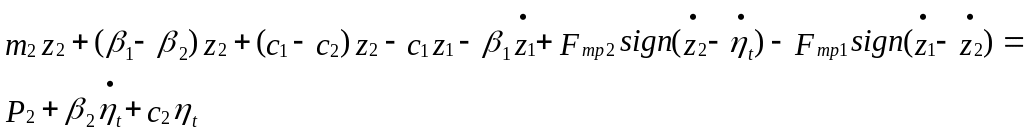(5.5)

Представим силы сухого трения зависящими от прогиба рессорного подвешивания, тогда получим

(5.6)

Тогда система дифференциальных уравнений описывающих колебания грузов, будет иметь вид

Будем искать решение системы уравнений на участке , где будем полагать, что , то есть после решения системы и вычисления всех параметров необходимо проверить знаки сигнатур и исправить их, если несовпадают.

При принятых значениях система примет вид

Разделим первое уравнение на и учитывая что

Разделим второе уравнение на и учитывая, что

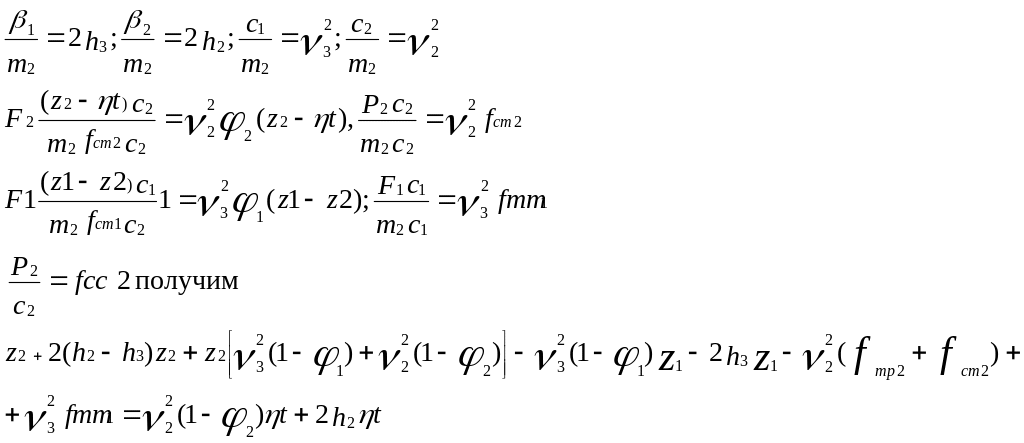
Где -соответственно стрелы трения от действующих сил трения F1 и F2

-коэффициенты относительного трения в первой

Применим для уравнений расщепление фазовых пространств: перенесем все переменные с z₂ в правую часть, скрестно перемножим уравнения, выполним операцию передачи производной (энергетического уровня) и приведем подобные члены. Тогда для автономного дифференциального уравнения, описывающего колебания первого груза на рассматриваемом участке времени, получим выражение

(5.11)

Где приняты обозначения:

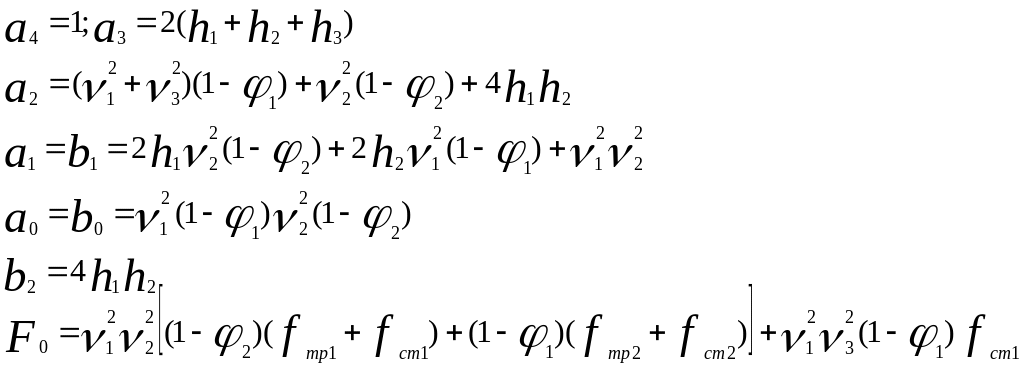
Уравнение является отделившимся, его общее и частное решение достаточно просто определяются. Из уравнения видно, что на рассматриваемом участке колебания происходят относительно положения, определяемого величиной

Уравнение получено в общем виде и если не учитывать силы, сухого и вязкого трения, силу тяжести

То получим уравнение вида

(5.12)

Рассмотрим общее решение уравнения (5.12), для чего, полагая z₁ = Ae^kl, дифференцируя его четыре раза, затем, сокращая на Ae^kl≠0 получим характеристическое уравнение в виде

Найдем корни уравнения

Как видно из частоты собственных колебаний не зависят от начальных условий задачи и определяются только параметрами системы. Анализируя корни уравнения , можно отметить, что они имеют мнимые части и, следовательно, круговые частоты. Поэтому движение груза представляет собой периодические колебания с определенной круговой частотой.

Для оценки вынужденных колебаний (5.11), примем . Тогда

, и уравнение (5,11) будет иметь вид

(5,15)

Пусть неровность является длинной, собственные колебания успевают затухнуть, а имеют место установившиеся вынужденные колебания. Тогда для вынужденных колебаний будем искать частное решение уравнения (5.15) в виде

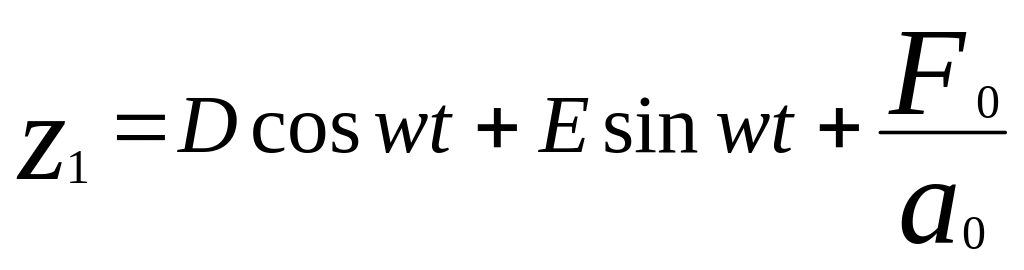
=const и движение происходит на рассматриваемом отрезке времени.

Дифференцируя выражение (5.16) четыре раза, подставляя полученные уравнения в (5.15), группируя коэффициенты соответственно при и , затем сокращая на ≠0 и ≠0, окончательно для вынужденных колебаний найдем

(5,17)

Вычислив значения D и E, мы нашли частное решение уравнения (5,15) для рассмотренного отрезка времени в виде (5.16). Зная решения для Z1 и подставляя его, например, в первое уравнение системы (5.9), аналогично найдём решения для z₂.

Таким образом, мы нашли решения для исходной системы. Зная z₁ z₂, ηt продифференцировав их, найдем значения сигнатур sign(z₁-z₂₎ и sign(z₁- ηt). Если найденные знаки отличаются от принятых нами в начале, то в полученных решениях перед φ и f_тп соответственно необходимо изменить знак.

Найденные аналитические решения позволяют дать полный анализ происходящему колебательному процессу, рассмотреть зоны затухающих колебаний и участки, где происходит генерирование амплитуд. Решение позволяет рассматривать широкий круг задач при различных возмущающих функциях и силах диссипации энергии.

Динамические силы в системе, их максимальные значения, приводящие к возникновению опасных ситуаций, угрожающих безопасности движения, соответственно определяются из выражений (5.1) и (5.3).

Рассмотрим теперь двухстепенную систему, имеющую кроме линейных, как было показано выше, угловые перемещения. На рис. 5.3 представлена расчетная схема экипажа.

Пусть система движется слева направо и в связях кузова реализуются упругие и диссипативные (сухого и вязкого трения) силы.

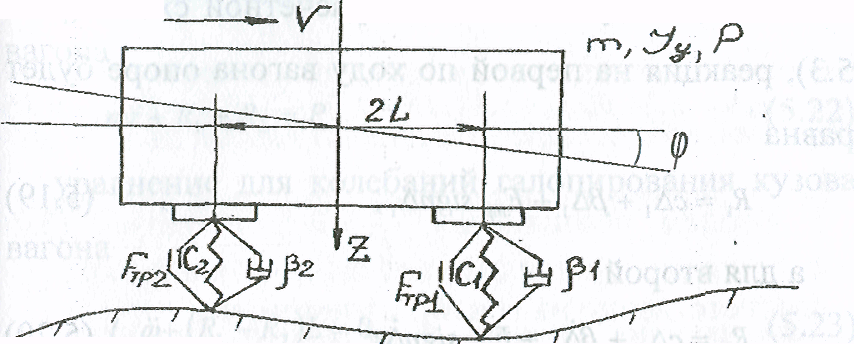
Рис. 5.3 Расчетная схема системы с 2-мя степенями свободы, линейными и угловыми координатами.

Следует отметить, что обычно в таких конструкциях β_l=β₂=β c_l=c₂=c так как кузов в конструктивном исполнении является симметричным. Неровность пути под каждым колесом будет иметь сдвиг по длине

В общем случае согласно расчетной схеме реакция на первом по ходу вагона опоре будет равна

Уравнение для колебаний подпрыгивания кузова вагона

Уравнение для колебаний галопирования кузова вагона

Где - физический момент инерции кузова вагона

Будем искать решение уравнений на участке , где будем полагать ,что

то есть в выражениях перед силами трения надо поставить знак минус.

После решения системы и вычисления всех параметров необходимо проверить правильность принятых значений сигнатур и исправить их, если есть несовпадения.

С учетом сказанного система будет иметь вид

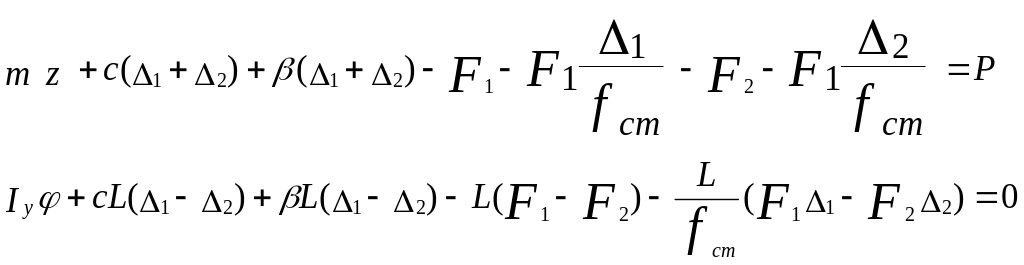
Введем обозначение сократим соответственно на m b m11 c учетом, что

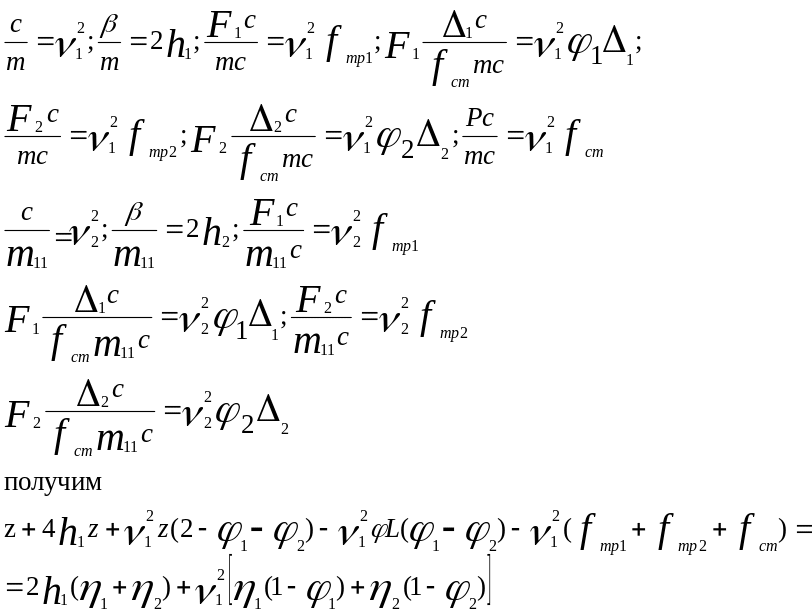
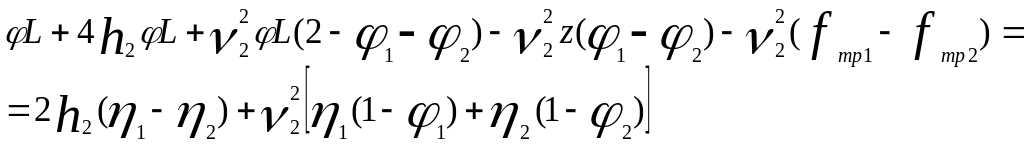(5,25)

Из уравнений (5.25) видно, что при каждое уравнение становится автономным. Но такой вид колебательного процесса возможен при равенстве постоянных значений сил трения F, =F₂,

Применив правило расщепления пространств или исключения переменных, можно определить из первого уравнения (5.25) угол галопирования кузова, продифференцировать два раза и подставив во второе уравнение (5.25), получим автономное уравнение для колебаний подпрыгивания кузова вагона.

Так как в железнодорожных экипажах обычно то есть

И то система уравнений разделяется на автономные уравнения

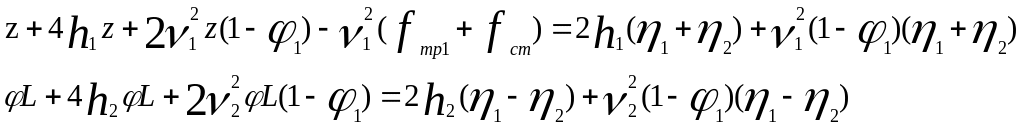
Анализируя однородные уравнения приходим к выводу, что их левые части идентичны и колебательные процессы на стадии затухания и генерирования амплитуд колебаний в основном определяются величинами . Колебания подпрыгивания происходят (при малых сопротивлениях движению) соответственно относительно положения

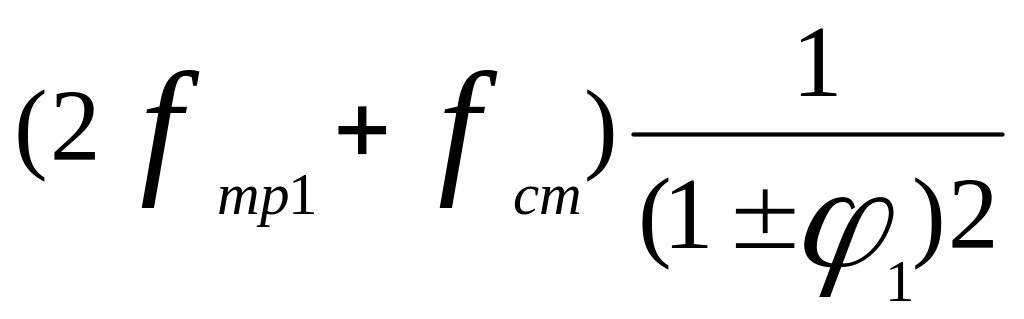
С учетом получим

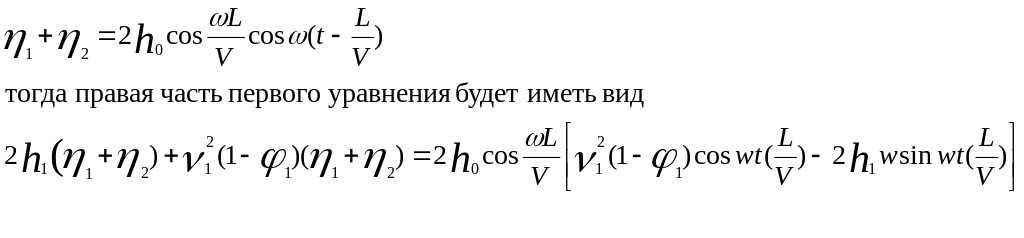
Будем искать частное решение первого неоднородного уравнения для оценки вынужденных колебаний подпрыгивания кузова вагона в виде

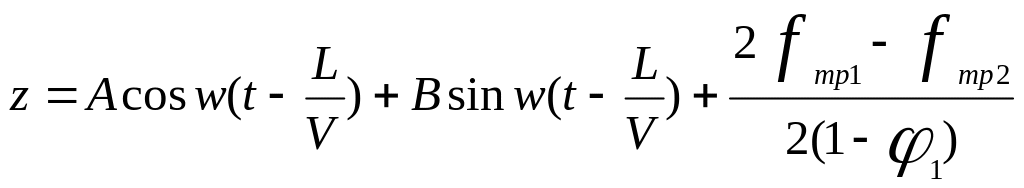
Продифференцируем два раза и подставим в уравнение с учетом правой части, тогда найдем

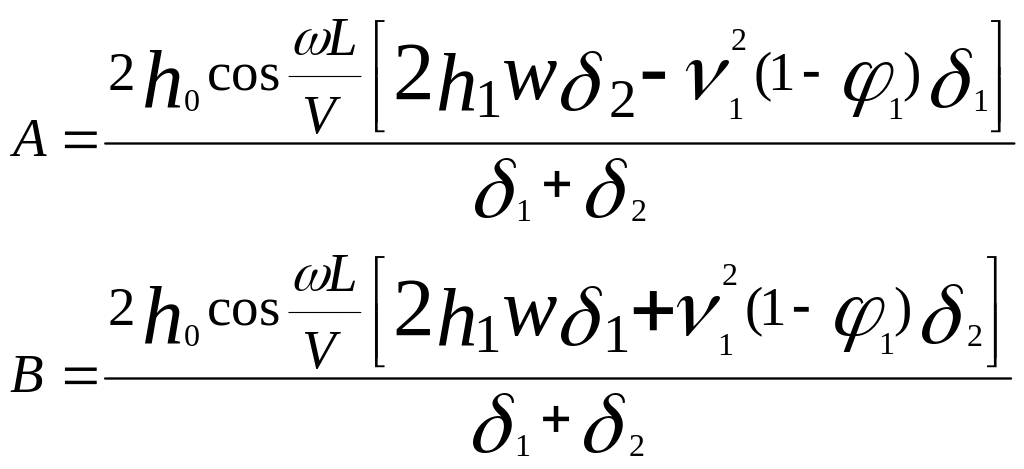(5,30)

Следовательно, для оценки амплитуд вынужденных колебаний подпрыгивания кузова вагона выражение будет иметь вид с учетом

Обозначим тогда получим

(5.31)

Уравнение (5.31) показывает, что на рассматриваемом отрезке времени колебания подпрыгивания происходят с максимальной амплитудой М относительно положения, определяемого последним членом уравнения (5.31). Колебания происходят со сдвигом по фазе на величину . При этом колебания на одних участках затухают, а на других - наоборот нарастают.

Так и получаются установившиеся вынужденные колебания. Аналогично находится решение для второго уравнения (5.26), где учитываются решения (5.18) и тогда

Вычислив z и φ, определяют

и и если эти значения совпадают с принятыми нами ранее, то значения перед и

Оставляют, а если знаки не совпадают, то в этом случае изменяют на обратный перед теми выражениями, где это произошло.