
Министерство образования и науки РФ
Магнитогорский государственный технический университет
им. Г.И.Носова
Кафедра математики, эконометрики и статистики
ИНТЕГРАЛЫ
Методическая разработка для студентов всех специальностей
Магнитогорск 2006
Печатается по решению кафедры МЭиС МГТУ
Интегралы: Методическая разработка (электронный вариант). Составитель: Терентьев А.Г. Магнитогорск, МГТУ, 2006. – 36 с.
Методическая разработка составлена на основе учебного пособия: Кузнецов В.А. Сборник задач по высшей математике, ТР. – М.: «Высшая школа», 1984.
В качестве образца выполнения индивидуального домашнего задания (ИДЗ) полностью приводятся решения всех задач варианта 31 с подробными разъяснениями и рекомендациями.
В ПРИЛОЖЕНИЯХ 1 – 30 (120 с.) к каждой задаче даётся пять вариантов ответов, один из которых является верным. Имеется определитель правильных ответов, что позволяет осуществить быстрый контроль.
Дан также образец заполнения титульного листа.
Методическая разработка предназначена студентам всех специальностей стационара и ОЗО.
Составитель: к. ф.-м. н. доцент Терентьев А.Г.
Рецензент: к. ф.-м. н. доцент Плышевская Т.К.
© Терентьев А.Г.
Образец заполнения титульного листа:
ИДЗ по теме «Интегралы»
Вариант 31
Выполнил ______ФИО _______ № группы_______________
Таблица ответов
№ задачи |
1 |
2 |
3 |
… |
19 |
20 |
21 |
22 |
№ ответа |
1 |
3 |
2 |
… |
4 |
5 |
2 |
3 |
К ЗАДАЧЕ 1.
Здесь надо применить метод интегрирования по частям в неопределенном интеграле:
![]() .
(*)
.
(*)
Естественно, надо твердо знать таблицу интегралов и правила интегрирования (свойства интегралов).
ЗАДАЧА 1.31
Найти неопределенный
интеграл
![]() .
.
Решение.
Интегрируем по частям, подобрав функции u и v следующим образом:

Тогда по формуле (*) получаем:
![]()
![]()
К ЗАДАЧЕ 2.
Здесь надо применить (причем дважды) метод интегрирования по частям в определенном интеграле:
![]() .
.
Запись
![]() означает разность
означает разность
![]() .
.
ЗАДАЧА 2.31
Вычислить определенный
интеграл:
![]() .
.
Решение.

![]()

![]()
![]()
![]()
![]()
К ЗАДАЧЕ 3.
Здесь используется метод замены переменной в неопределен-ном интеграле:
![]()
Надо постараться «увидеть» в интеграле функцию и ее производную (или «часть» ее производной).
В некоторых интегралах надо воспользоваться формулой:
![]()
ЗАДАЧА 3.31
Найти неопределенный
интеграл:
![]()
Решение.

![]()
![]()
Поэтому:
![]()
![]()
К ЗАДАЧЕ 4.
Надо применить метод замены переменной в определенном интеграле.
ЗАДАЧА 4.31
Вычислить определенный
интеграл
![]() .
.
Решение.

![]()
Ответ: 23,1.
К ЗАДАЧАМ 5, 6 и 7.
Здесь речь идет об интегрировании рациональных дробей. В задаче 5 дробь – неправильная. Поэтому вначале надо выделить целую часть. Правильную часть надо разложить на элементарные дроби, которые уже интегрируются сравнительно легко.
ЗАДАЧА 5.31
Найти неопределенный
интеграл
![]() .
.
Решение.
Здесь степень числителя равняется степени знаменателя. Значит, дробь неправильная. Поэтому надо выделить целую часть, поделив многочлен на многочлен «уголком».
Заметим, что
![]() .
Теперь:
.
Теперь:
 .
.
Поэтому:
![]()
![]()
Разложим теперь правильную дробь на элементарные дроби I типа:
![]() ,
,
![]() .
.
Подставляя нули знаменателя в обе части этого равенства, практически легко и быстро получаем неопределенные коэффициенты:
 .
.
Теперь продолжаем прерванное выше равенство:
![]()
![]()


Задача 6.31
Найти неопределенный интеграл:
![]() .
.
Решение.
Здесь дробь правильная; разлагаем на элементарные дроби I и II типов:
![]() ;
;
![]()
![]() .
(*)
.
(*)
Неопределенные коэффициенты, в основном, находят двумя способами:
уравниванием коэффициентов левой и правой частей (*) при одинаковых степенях буквы х и
подстановкой в левую и правую части конкретных значений х.
Зачастую полезно комбинировать эти способы.
 .
.
Итак:
![]()
![]()
Ответ:
![]() .
.
Замечание.
Результат мы могли получить быстрее,
если бы мы сразу увидели, что числитель
дроби можно представить в виде:
![]() .
.
Задача 7.31
Найти неопределенный интеграл
![]()
Решение.
Дробь – правильная. Разлагаем на элементарные дроби III типа:
![]() ;
;
![]() .
(*)
.
(*)
Используем первый способ отыскания неопределенных коэффициентов – уравниваем в (*) коэффициенты левой и правой частей при одинаковых степенях буквы х:
 .
.
Номера справа указывают очередность отыскания коэффициентов из системы.
Теперь:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
К ЗАДАЧЕ 8.
К интегралам вида
![]() ,
где R
– рациональное выражение, применяют
универсальную
подстановку:
,
где R
– рациональное выражение, применяют
универсальную
подстановку:
![]() .
.
Тогда
![]() .
Кроме того:
.
Кроме того:
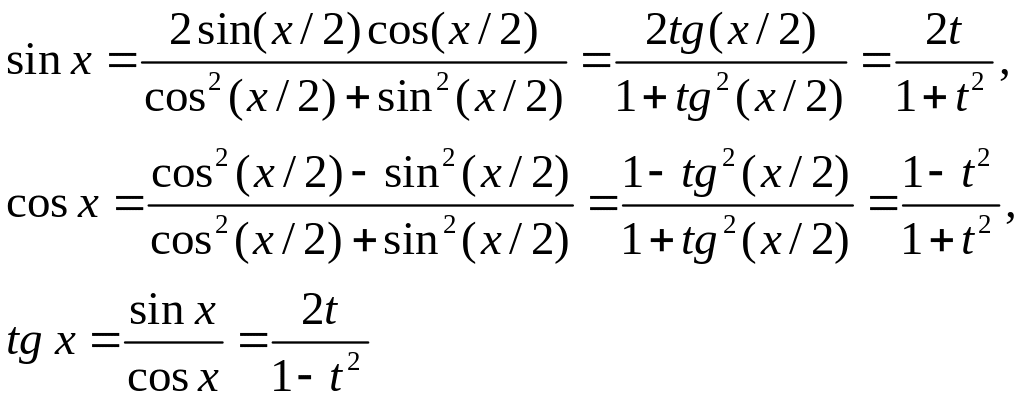
Задача 8.31
Вычислить определенный
интеграл:
![]() .
.
Решение.




![]()
![]()

![]()
Ответ:
![]()
Заметьте, что универсальная подстановка приводит к интегралу от рациональной дроби. У нас получилась правильная рациональная дробь, которую мы разложили на элементарные дроби, не прибегая к методу неопределенных коэффициентов. Для компактной записи ответа мы применили формулу:
![]() .
.
К ЗАДАЧЕ 9.
К интегралам вида
![]() ,
где R
– рациональное выражение, применяют
подстановку:
,
где R
– рациональное выражение, применяют
подстановку:
![]() .
.
Тогда
![]() .
Кроме того:
.
Кроме того:

ЗАДАЧА 9.31
Вычислить определенный
интеграл:
 .
.
Решение.




Ответ:
![]()
Здесь мы тоже легко разложили рациональную дробь на простейшие (элементарные) дроби.
К ЗАДАЧЕ 10.
Интегралы вида
![]() ,
где R
– рациональное выражение, «берутся»
понижением
степени по формулам:
,
где R
– рациональное выражение, «берутся»
понижением
степени по формулам:
![]() .
.
ЗАДАЧА 10.31
Вычислить определенный
интеграл:
![]() .
.
Решение.


![]()

Ответ:
![]()
К ЗАДАЧЕ 11.
Интегралы, в основном, однотипны: они приводятся к виду
 .
.
Надо сделать
замену:
![]() При этом
При этом
коэффициенты а, в, с и d в задачах подобраны так, что можно
сразу найти
![]() ,
не находя отдельно х.
,
не находя отдельно х.
ЗАДАЧА 11.31
Вычислить определенный интеграл:
 .
.
Решение.

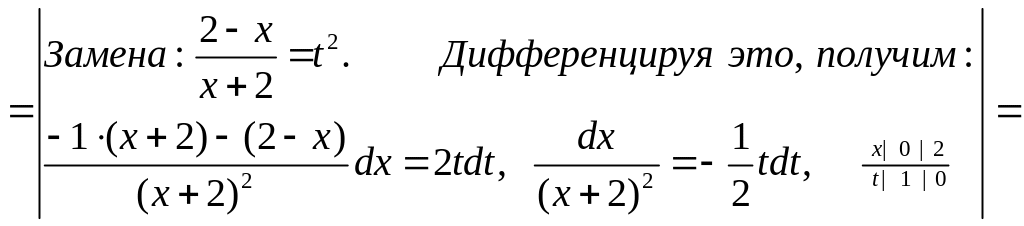
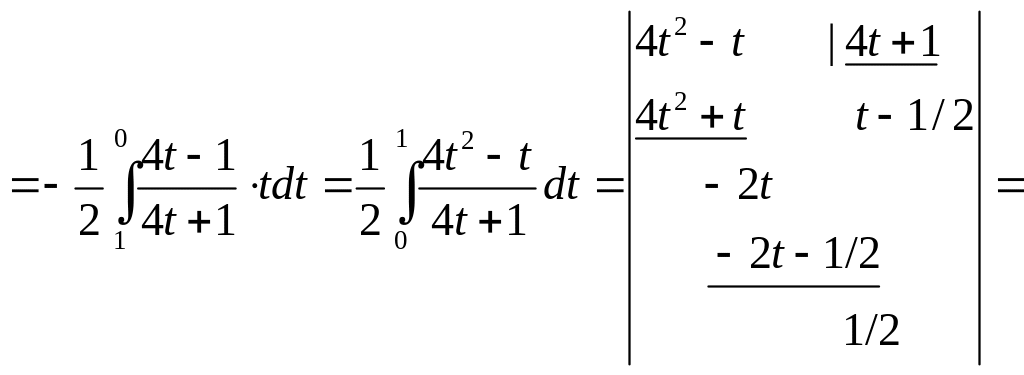
![]()

Ответ:
![]()
К ЗАДАЧЕ 12.
Здесь приведены интегралы трех типов:
![]() ,
,
![]()
![]()
которые рационализируются соответственно подстановками:
![]() .
.
ЗАДАЧА 12.31
Вычислить определенный
интеграл:
![]() .
.
Решение.

![]()
![]()

Ответ:
![]()
К ЗАДАЧЕ 13.
Интеграл
![]() рациональные
числа, называется интегралом от
дифференциального
бинома. Доказано
выдающимся русским математиком Пафнутием
Львовичем Чебышевым (1821-1894), что такой
интеграл допускает рационализацию
только в трех случаях:
рациональные
числа, называется интегралом от
дифференциального
бинома. Доказано
выдающимся русским математиком Пафнутием
Львовичем Чебышевым (1821-1894), что такой
интеграл допускает рационализацию
только в трех случаях:
р - целое число. Надо осуществить подстановку
 ,
где s
- знаменатель дроби
,
где s
- знаменатель дроби
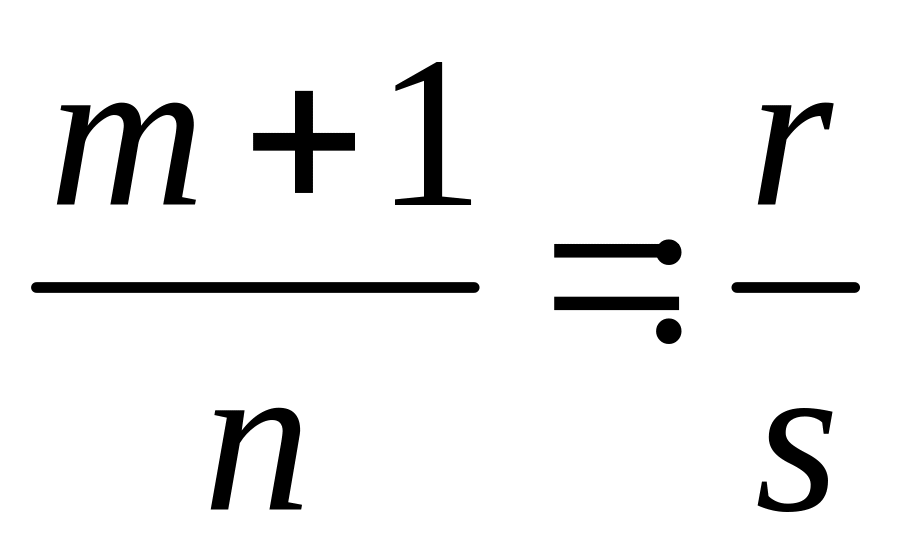 ;
; - целое число. Тогда
– подстановка
- целое число. Тогда
– подстановка
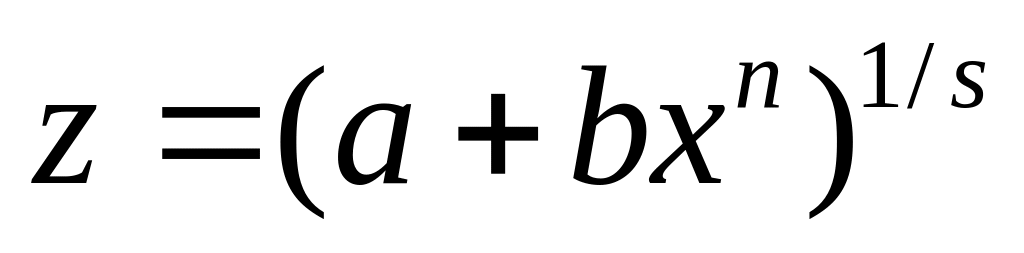 ,
где s
- знаменатель дроби
,
где s
- знаменатель дроби
 ;
; - целое число.
Подстановка
- целое число.
Подстановка
 ,
где s
- знаменатель дроби
.
,
где s
- знаменатель дроби
.
Внимание! В пособии: Кузнецов Л.А. Сборник задач по высшей математике (ТР), в № 13.21 (с. 60) опечатка: надо под радикалом в числителе за скобками поставить показатель степени 4.
